Balanced histogram thresholding

In image processing, the balanced histogram thresholding method (BHT),[1] is a very simple method used for automatic image thresholding. Like Otsu's Method[2] and the Iterative Selection Thresholding Method,[3] this is a histogram based thresholding method. This approach assumes that the image is divided in two main classes: The background and the foreground. The BHT method tries to find the optimum threshold level that divides the histogram in two classes.

Original image.
Thresholded image.
Evolution of the method.

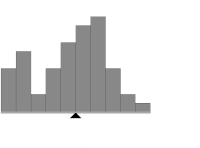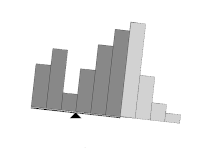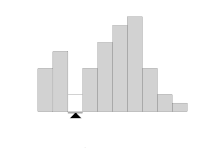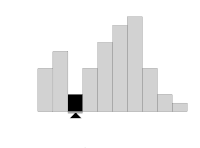
This method weighs the histogram, checks which of the two sides is heavier, and removes weight from the heavier side until it becomes the lighter. It repeats the same operation until the edges of the weighing scale meet.

Given its simplicity, this method is a good choice as a first approach when presenting the subject of automatic image thresholding.

Algorithm

The following listing, in C notation, is a simplified version of the Balanced Histogram Thresholding method:

int BHThreshold(int[] histogram) {
    i_m = (int)((i_s + i_e) / 2.0f); // center of the weighing scale I_m
    w_l = get_weight(i_s, i_m + 1, histogram); // weight on the left W_l
    w_r = get_weight(i_m + 1, i_e + 1, histogram); // weight on the right W_r
    while (i_s <= i_e) {
        if (w_r > w_l) { // right side is heavier
            w_r -= histogram[i_e--];
            if (((i_s + i_e) / 2) < i_m) {
                w_r += histogram[i_m];
                w_l -= histogram[i_m--];
            }
        } else if (w_l >= w_r) { // left side is heavier
            w_l -= histogram[i_s++]; 
            if (((i_s + i_e) / 2) >= i_m) {
                w_l += histogram[i_m + 1];
                w_r -= histogram[i_m + 1];
                i_m++;
            }
        }
    }
    return i_m;
}

The following, is a possible implementation in the Python language:

def bht(hist, min_count: int = 5) -> int:
    """Balanced histogram thresholding."""
    n_bins = len(hist)  # assumes 1D histogram
    h_s = 0
    while hist[h_s] < min_count:
        h_s += 1  # ignore small counts at start
    h_e = n_bins - 1
    while hist[h_e] < min_count:
        h_e -= 1  # ignore small counts at end
    # use mean intensity of histogram as center; alternatively: (h_s + h_e) / 2)
    h_c = int(round(np.average(np.linspace(0, 2 ** 8 - 1, n_bins), weights=hist)))
    w_l = np.sum(hist[h_s:h_c])  # weight in the left part
    w_r = np.sum(hist[h_c : h_e + 1])  # weight in the right part

    while h_s < h_e:
        if w_l > w_r:  # left part became heavier
            w_l -= hist[h_s]
            h_s += 1
        else:  # right part became heavier
            w_r -= hist[h_e]
            h_e -= 1
        new_c = int(round((h_e + h_s) / 2))  # re-center the weighing scale

        if new_c < h_c:  # move bin to the other side
            w_l -= hist[h_c]
            w_r += hist[h_c]
        elif new_c > h_c:
            w_l += hist[h_c]
            w_r -= hist[h_c]

        h_c = new_c

    return h_c

References
  1. A. Anjos and H. Shahbazkia. Bi-Level Image Thresholding - A Fast Method. BIOSIGNALS 2008. Vol:2. P:70-76.
  2. Nobuyuki Otsu (1979). "A threshold selection method from gray-level histograms". IEEE Trans. Sys., Man., Cyber. 9: 62–66.
  3. Ridler TW, Calvard S. (1978) Picture thresholding using an iterative selection method, IEEE Trans. System, Man and Cybernetics, SMC-8: 630-632.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.