Closing (morphology)

In mathematical morphology, the closing of a set (binary image) A by a structuring element B is the erosion of the dilation of that set,

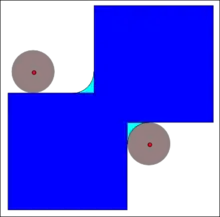
The closing of the dark-blue shape (union of two squares) by a disk, resulting in the union of the dark-blue shape and the light-blue areas.

where and denote the dilation and erosion, respectively.

In image processing, closing is, together with opening, the basic workhorse of morphological noise removal. Opening removes small objects, while closing removes small holes.

Properties
  • It is idempotent, that is, .
  • It is increasing, that is, if , then .
  • It is extensive, i.e., .
  • It is translation invariant.

See also

Bibliography
  • Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0-12-637240-3 (1982)
  • Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, ISBN 0-12-637241-1 (1988)
  • An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.