Dihedral (aeronautics)
In aeronautics, dihedral is the angle between the left and right wings (or tail surfaces) of an aircraft. "Dihedral" is also used to describe the effect of sideslip on the rolling of the aircraft.
_taxying_for_take_off_at_Bristol_Airport%252C_England_14May2019.jpg.webp)
.svg.png.webp)

Dihedral angle is the upward angle from horizontal of the wings or tailplane of a fixed-wing aircraft. "Anhedral angle" is the name given to negative dihedral angle, that is, when there is a downward angle from horizontal of the wings or tailplane of a fixed-wing aircraft.
Dihedral angle has a strong influence on dihedral effect, which is named after it. Dihedral effect is the amount of roll moment produced in proportion to the amount of sideslip. Dihedral effect is a critical factor in the stability of an aircraft about the roll axis (the spiral mode). It's also pertinent to the nature of an aircraft's Dutch roll oscillation and to maneuverability about the roll axis.
Longitudinal dihedral is a comparatively obscure term related to the pitch axis of an airplane. It is the angle between the zero-lift axis of the wing and the zero-lift axis of the horizontal tail. Longitudinal dihedral can influence the nature of controllability about the pitch axis and the nature of an aircraft's phugoid-mode oscillation.
When the term "dihedral" (of an aircraft) is used by itself it is usually intended to mean "dihedral angle". However, context may otherwise indicate that "dihedral effect" is the intended meaning.
Dihedral angle vs. dihedral effect
Dihedral angle is the upward angle from horizontal of the wings of a fixed-wing aircraft, or of any paired nominally-horizontal surfaces on any aircraft. The term can also apply to the wings of a bird. Dihedral angle is also used in some types of kites such as box kites. Wings with more than one angle change along the full span are said to be polyhedral.
Dihedral angle has important stabilizing effects on flying bodies because it has a strong influence on the dihedral effect.
Dihedral effect[1] of an aircraft is a rolling moment resulting from the vehicle having a non-zero angle of sideslip. Increasing the dihedral angle of an aircraft increases the dihedral effect on it. However, many other aircraft parameters also have a strong influence on dihedral effect. Some of these important factors are: wing sweep, vertical center of gravity, and the height and size of anything on an aircraft that changes its sidewards force as sideslip changes.
Longitudinal dihedral
Dihedral angle on an aircraft almost always implies the angle between two paired surfaces, one on each side of the aircraft. Even then, it is almost always between the left and right wings. However, mathematically dihedral means the angle between any two planes. So, in aeronautics, in one case, the term "dihedral" is applied to mean the difference in angles between two front-to-back surfaces:
Longitudinal dihedral is the difference between the angle of incidence of the wing root chord and angle of incidence of the horizontal tail root chord.
Longitudinal dihedral can also mean the angle between the zero-lift axis of the wing and the zero-lift axis of the horizontal tail instead of between the root chords of the two surfaces. This is the more meaningful usage because the directions of zero-lift are pertinent to longitudinal trim and stability while the directions of the root chords are not.
History
In geometry, dihedral angle is the angle between two planes. Aviation usage differs slightly from usage in geometry. In aviation, the usage "dihedral" evolved to mean the positive, up angle between the left and right wings, while usage with the prefix "an-" (as in "anhedral") evolved to mean the negative, down angle between the wings.
The aerodynamic stabilizing qualities of a dihedral angle were described in an influential 1810 article by Sir George Cayley.[2]
Uses of dihedral angle and dihedral effect
Aircraft stability analysis
In analysis of aircraft stability, the dihedral effect is also a stability derivative called Cl[note 1] meaning the change in rolling moment coefficient (the "Cl")[note 2] per degree (or radian) of change in sideslip angle (the "").
Provision of stability
The purpose of dihedral effect is to contribute to stability in the roll axis. It is an important factor in the stability of the spiral mode which is sometimes called "roll stability".[note 3] The dihedral effect does not contribute directly to the restoring of "wings level", but it indirectly helps restore "wings level" through its effect on the spiral mode of motion described below.
Wing clearance
Aircraft designers may increase dihedral angle to provide greater clearance between the wing tips and the runway. This is of particular concern with swept-wing aircraft, whose wingtips could hit the runway on rotation/touchdown. In military aircraft dihedral angle space may be used for mounting materiel and drop-tanks on wing hard points, especially in aircraft with low wings. The increased dihedral effect caused by this design choice may need to be compensated for, perhaps by decreasing the dihedral angle on the horizontal tail.
Using dihedral angle to adjust dihedral effect
During design of a fixed-wing aircraft (or any aircraft with horizontal surfaces), changing dihedral angle is usually a relatively simple way to adjust the overall dihedral effect. This is to compensate for other design elements' influence on the dihedral effect. These other elements (such as wing sweep, vertical mount point of the wing, etc.) may be more difficult to change than the dihedral angle. As a result, differing amounts of dihedral angle can be found on different types of fixed-wing aircraft. For example, the dihedral angle is usually greater on low-wing aircraft than on otherwise-similar high-wing aircraft. This is because "highness" of a wing (or "lowness" of vertical center of gravity compared to the wing) naturally creates more dihedral effect itself. This makes it so less dihedral angle is needed to get the amount of dihedral effect needed.
Common confusions
Dihedral effect is defined simply to be the rolling moment caused by sideslip and nothing else. Rolling moments caused by other things that may be related to sideslip have different names.
Dihedral effect is not caused by yaw rate, nor by the rate of sideslip change. Since dihedral effect is noticed by pilots when "rudder is applied", many pilots and other near-experts explain that the rolling moment is caused by one wing moving more quickly through the air and one wing less quickly. Indeed, these are actual effects, but they are not the dihedral effect, which is caused by being at a sideslip angle, not by getting to one. These other effects are called "rolling moment due to yaw rate" and "rolling moment due to sideslip rate" respectively.
Dihedral effect is not roll stability in and of itself. Roll stability is less-ambiguously termed "spiral mode stability" and dihedral effect is a contributing factor to it.
How dihedral angle creates dihedral effect and stabilizes the spiral mode
The dihedral angle contributes to the total dihedral effect of the aircraft. In turn, the dihedral effect contributes to stability of the spiral mode. A stable spiral mode will cause the aircraft to eventually return to a nominally "wings level" bank angle when the angle of the wings is disturbed to become off-level.[note 4]
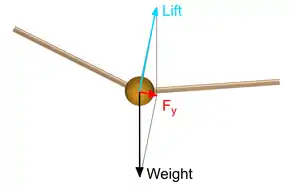
If a disturbance causes an aircraft to roll away from its normal wings-level position as in Figure 1, the aircraft will begin to move somewhat sideways toward the lower wing.[3] In Figure 2, the airplane's flight path has started to move toward its left while the nose of the airplane is still pointing in the original direction. This means that the oncoming air is arriving somewhat from the left of the nose. The airplane now has sideslip angle in addition to the bank angle. Figure 2 shows the airplane as it presents itself to the oncoming air.
How dihedral angle creates rolling moment from sideslip (dihedral effect)
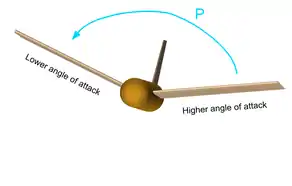
In Figure 2, the sideslip conditions produce greater angle of attack on the forward-yawed wing and smaller angle of attack on the rearward-yawed wing. This alteration of angle of attack by sideslip is visible in Figure 2. As greater angle of attack produces more lift (in the usual case, when the wing is not near stalling), the forward wing will have more lift and the rearward wing will have less lift. This difference in lift between the wings is a rolling moment, and it's caused by the sideslip. It's a contribution to the total dihedral effect of the aircraft.
How dihedral effect stabilizes the spiral mode
The rolling moment created by the sideslip (labeled as "P") tends to roll the aircraft back to wings level. More dihedral effect tries to roll the wings in the "leveling" direction more strongly, and less dihedral effect tries to roll the wings in the "leveling" direction less strongly. Dihedral effect helps stabilize the spiral mode by tending to roll the wings toward level in proportion to the amount of sideslip that builds up. It's not the whole picture however. At the same time that angle of sideslip is building up, the vertical fin is trying to turn the nose back into the wind, much like a weathervane, minimizing the amount of sideslip that can be present. If there is no sideslip, there can be no restoring rolling moment. If there is less sideslip, there is less restoring rolling moment. Yaw stability created by the vertical fin opposes the tendency for dihedral effect to roll the wings back level by limiting sideslip.
The spiral mode is the tendency to slowly diverge from, or the tendency to slowly return to wings level. If the spiral mode is stable, the aircraft will slowly return to wings-level, if it is unstable, the aircraft will slowly diverge from wings-level. Dihedral effect and yaw stability are the two primary factors that affect the stability of the spiral mode, although there are other factors that affect it less strongly.
Other factors contributing to dihedral effect

Factors of design other than dihedral angle also contribute to dihedral effect. Each increases or decreases total aircraft dihedral effect to a greater or lesser degree.
Sweepback
Wing sweepback also increases dihedral effect. This is one reason for anhedral configuration on aircraft with high sweep angle, as well as on some airliners, even on low-wing aircraft such as the Tu-134 and Tu-154, with the small German 1930s – 1945 biplanes of the Bücker Flugzeugbau, the Bucker Jungmann two-seat trainer and more famous Bücker Jungmeister aerobatic competition biplane, both having approximately 11° of wing sweepback giving both designs a degree of dihedral effect, beyond the small amount of dihedral both biplanes' designs also featured.
Vertical position of the center of mass
The center of mass, usually called the center of gravity or "CG", is the balance point of an aircraft. If suspended at this point and allowed to rotate, a body (aircraft) will be balanced. The front-to-back location of the CG is of primary importance for the general stability of the aircraft, but the vertical location has important effects as well.
The vertical location of the CG changes the amount of dihedral effect. As the "vertical CG" moves lower, dihedral effect increases. This is caused by the center of lift and drag being further above the CG and having a longer moment arm. So, the same forces that change as sideslip changes (primarily sideforce, but also lift and drag) produce a larger moment about the CG of the aircraft. This is sometimes referred to as the pendulum effect.[note 5]
An extreme example of the effect of vertical CG on dihedral effect is a paraglider. The dihedral effect created by the very low vertical CG more than compensates for the negative dihedral effect created by the strong anhedral[note 6] of the necessarily strongly downward curving wing.
Effects of too much dihedral effect
A side effect of too much dihedral effect, caused by excessive dihedral angle among other things, can be yaw-roll coupling (a tendency for an aircraft to Dutch roll). This can be unpleasant to experience, or in extreme conditions it can lead to loss of control or can overstress an aircraft.
Anhedral and polyhedral
Anhedral


Military fighter aircraft often have near zero or even anhedral angle reducing dihedral effect and hence reducing the stability of the spiral mode. This increases maneuverability which is desirable in fighter-type aircraft.
Anhedral angles are also seen on aircraft with a high mounted wing, such as the very large Antonov An-124 and Lockheed Galaxy cargo aircraft. In such designs, the high mounted wing is above the aircraft's center of gravity which confers extra dihedral effect due to the pendulum effect (also called the keel effect) and so additional dihedral angle is often not required. Such designs can have excessive dihedral effect and so be excessively stable in the spiral mode, so anhedral angle on the wing is added to cancel out some of the dihedral effect so that the aircraft can be more easily maneuvered.
Polyhedral

Most aircraft have been designed with planar wings with simple dihedral (or anhedral). Some older aircraft such as the Vought F4U Corsair and the Beriev Be-12 were designed with gull wings bent near the root. Modern polyhedral wing designs generally bend upwards near the wingtips (also known as tip dihedral), increasing dihedral effect without increasing the angle the wings meet at the root, which may be restricted to meet other design criteria.
Polyhedral is seen on gliders and some other aircraft. The McDonnell Douglas F-4 Phantom II is one such example, unique among jet fighters for having dihedral wingtips. This was added after flight testing of the flat winged prototype showed the need to correct some unanticipated spiral mode instability – angling the wingtips, which were already designed to fold up for carrier operations, was a more practical solution than re-engineering the entire wing.[4]
References
Footnotes
- Pronounced "See-ell-beta".
- A rolling moment coefficient is a "normalization" of the rolling moment. Rolling moment has units of force times length. The rolling moment coefficient is normalized so it has no units. This is done by dividing the moment by wing area and by wing span and by dynamic pressure.
- "Roll Stability" is an ambiguous term requiring context to discern the intended meaning of the user. It usually means "Spiral Mode Stability", but it is also often misused to mean dihedral effect or dihedral angle, both of which are not "stability" themselves, though they contribute to spiral mode stability.
- In the spiral mode, if it is unstable, the aircraft will slowly, then more rapidly, diverge from "nominal wings-level" if the pilot makes no control inputs. If the spiral mode is stable and the pilot makes no inputs, when the aircraft starts from a banked attitude, it will return close to wings-level by itself.
- The "pendulum effect" is also less commonly called the "keel effect".
- The downward curve of a paraglider wing could be termed "continuous polyanhedral".
Notes
- Roskam, Jan (1979). "4.1.7". Airplane Flight Dynamics and Automatic Flight Controls. 1. Ottawa, Kansas: Roskam Aviation and Engineering Corporation. p. 139. Library of Congress Catalog Card Number: 78-31382
- "This angular form, with the apex downward, is the chief basis of stability in aerial navigation . . . and this most effectively prevents any rolling of the machine from side to side." George Cayley. On Aerial Navigation. (part II). Journal of Natural Philosophy, Chemistry, and the Arts., vol. 25 (Feb, 1810), pp. 81-87. As reprinted in Gibbs-Smith, Charles H. Sir George Cayley's Aeronautics, 1796-1855. HMSO. 1962. page 223 has the quote. Online at NASA (pdf) Archived May 11, 2013, at the Wayback Machine
- Etkin, Bernard; Dynamics of Flight ;Section 3.10; 1982; ISBN 0-471-08936-2
- Donald, David and Jon Lake, eds. McDonnell F-4 Phantom: Spirit in the Skies. London: AIRtime Publishing, 2002. ISBN 1-880588-31-5.
External links
- http://www.aeroexperiments.org/washoutbillow.shtml
- Demonstration of dihedral effect on Wolfram Demonstrations Project
- Video explanation on Real Engineering YouTube channel