Dini's surface

In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere.[1] It is named after Ulisse Dini[2] and described by the following parametric equations:[3]

${\displaystyle {\begin{aligned}x&=a\cos u\sin v\\y&=a\sin u\sin v\\z&=a\left(\cos v+\ln \tan {\frac {v}{2}}\right)+bu\end{aligned}}}$

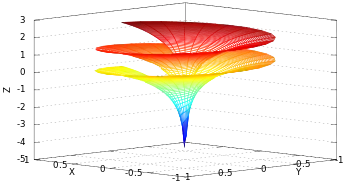
Dini's surface with 0 ≤ u ≤ 4π and 0.01 ≤ v ≤ 1 and constants a = 1.0 and b = 0.2.

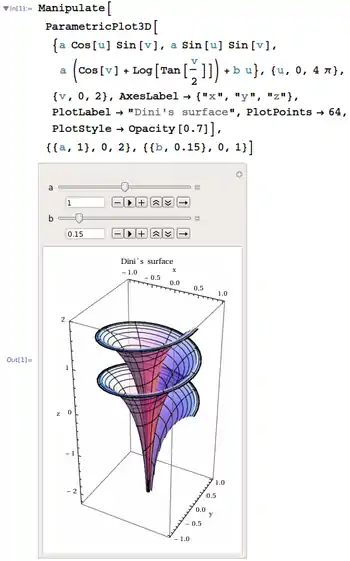
Dini's surface plotted with adjustable parameters by Wolfram Mathematica program

Another description is a helicoid constructed from the tractrix.[4]