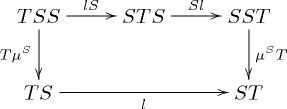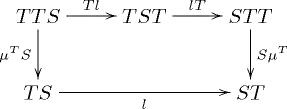Distributive law between monads
In category theory, an abstract branch of mathematics, distributive laws between monads are a way to express abstractly that two algebraic structures distribute one over the other one.
Suppose that and are two monads on a category C. In general, there is no natural monad structure on the composite functor ST. However, there is a natural monad structure on the functor ST if there is a distributive law of the monad S over the monad T.
Formally, a distributive law of the monad S over the monad T is a natural transformation
such that the diagrams
commute.
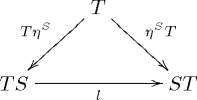
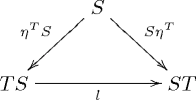
This law induces a composite monad ST with
- as multiplication: ,
- as unit: .
See also
References
- Beck, Jon (1969). "Distributive laws". Seminar on Triples and Categorical Homology Theory, ETH 1966/67. Lecture Notes in Mathematics. 80. pp. 119–140. doi:10.1007/BFb0083084. ISBN 978-3-540-04601-1.
- BBarr, Michael; Wells, Charles (1985). Toposes, Triples and Theories (PDF). Springer-Verlag. ISBN 0-387-96115-1. Archived from the original (PDF) on 2011-05-14.
- Distributive law in nLab
- Böhm, G. (2005). "Internal bialgebroids, entwining structures and corings". Algebraic Structures and Their Representations. Contemporary Mathematics. 376. pp. 207–226. arXiv:math.QA/0311244. ISBN 9780821836309.
- Brzeziński, T.; Majid, S. (1998). "Coalgebra bundles". Comm. Math. Phys. 191 (2): 467–492. arXiv:q-alg/9602022. Bibcode:1998CMaPh.191..467B. doi:10.1007/s002200050274. S2CID 189829500.
- Brzezinski, Tomasz; Wisbauer, Robert (2003). Corings and Comodules. London Mathematical Society Lecture Note Series. 309. Cambridge University Press. ISBN 978-0-521-53931-9.
- Fox, T.F.; Markl, M. (1997). "Distributive laws, bialgebras, and cohomology". Operads: Proceedings of Renaissance Conferences. Contemporary Mathematics. 202. American Mathematical Society. pp. 167–205. ISBN 9780821805138.
- Lack, S. (2004). "Composing PROPS". Theory Appl. Categ. 13 (9): 147–163.
- Lack, S.; Street, R. (2002). "The formal theory of monads II". J. Pure Appl. Algebra. 175 (1–3): 243–265. doi:10.1016/S0022-4049(02)00137-8.
- Markl, M. (1996). "Distributive laws and Koszulness". Annales de l'Institut Fourier. 46 (2): 307–323. doi:10.5802/aif.1516. Zbl 0853.18005.
- Street, R. (1972). "The formal theory of monads". J. Pure Appl. Alg. 2 (2): 149–168. doi:10.1016/0022-4049(72)90019-9.
- Škoda, Z. (2004). "Distributive laws for monoidal categories". arXiv:math/0406310.
- — (2007). "Equivariant monads and equivariant lifts versus a 2-category of distributive laws". arXiv:0707.1609 [math.CT].
- — (2008). "Bicategory of entwinings". arXiv:0805.4611 [math.RA].
- — (2009). "Some equivariant constructions in noncommutative geometry". Georgian Math. J. 16 (1): 183–202. arXiv:0811.4770. doi:10.1515/GMJ.2009.183 (inactive 2021-01-15).CS1 maint: DOI inactive as of January 2021 (link)
- Wisbauer, R. (2008). "Algebras versus coalgebras". Appl. Categ. Structures. 16 (1–2): 255–295. doi:10.1007/s10485-007-9076-5. S2CID 8150337.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.