Exposed point

In mathematics, an exposed point of a convex set ${\displaystyle C}$ is a point ${\displaystyle x\in C}$ at which some continuous linear functional attains its strict maximum over ${\displaystyle C}$. Such a functional is then said to expose ${\displaystyle x}$. There can be many exposing functionals for ${\displaystyle x}$. The set of exposed points of ${\displaystyle C}$ is usually denoted ${\displaystyle \exp(C)}$.

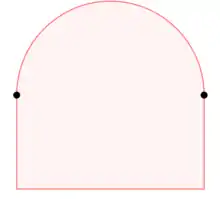
The two distinguished points are examples of extreme points of a convex set that are not exposed

A stronger notion is that of strongly exposed point of ${\displaystyle C}$ which is an exposed point ${\displaystyle x\in C}$ such that some exposing functional ${\displaystyle f}$ of ${\displaystyle x}$ attains its strong maximum over ${\displaystyle C}$ at ${\displaystyle x}$, i.e. for each sequence ${\displaystyle (x_{n})\subset C}$ we have the following implication: ${\displaystyle f(x_{n})\to \max f(C)\Longrightarrow \|x_{n}-x\|\to 0}$. The set of all strongly exposed points of ${\displaystyle C}$ is usually denoted ${\displaystyle \operatorname {str} \exp(C)}$.

There are two weaker notions, that of extreme point and that of support point of ${\displaystyle C}$.