Geological structure measurement by LiDAR
Geological structure measurement by LiDAR technology is a remote sensing method applied in structural geology. It enables monitoring and characterisation of rock bodies.[1] This method's typical use is to acquire high resolution structural and deformational data for identifying geological hazards risk, such as assessing rockfall risks or studying pre-earthquake deformation signs.

Geological structures are the results of tectonic deformations, which control landform distribution patterns. These structures include folds, fault planes, size, persistence, spatial variations, and numbers of the rock discontinuities in a particular region.[1] These discontinuity features significantly impact slope stability, causing slope failures or separating a rock mass into intact rock blocks (rockfall).[2] Some displaced blocks along faults are signs of earthquakes.
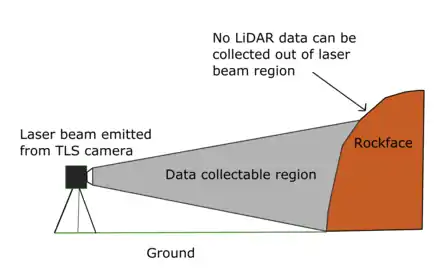
Conventionally, geotechnical engineers carried out rock discontinuity studies manually. In post geological hazards studies, such as rockfall, the rockfall source areas are dangerous and are difficult to access, severely hindering the ability to carry out detailed structural measurements and volumetric calculations necessary for hazard assessment.[3] By using LiDAR, geological structures can be evaluated remotely, enabling a 3-D investigation of slopes with virtual outcrops.
LiDAR technology (Light Detection and Ranging) is a remote sensing technique that obtains precise 3-D information and distance.[4] The laser receptor calculates the distance by the travelling time between emitting and receiving laser pulses.[4] LiDAR produces topographic maps, and it is useful for assessing the natural environment.
| Useful Links |
| Related Disciplines |
| Portal |
|
Importance of measuring geological structures by LiDAR
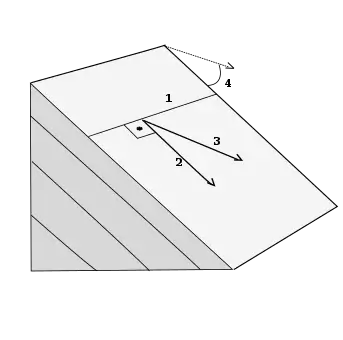
Geological structures are responsible for providing distinct physical properties to rock masses. Discontinuous properties and plate tectonic forces may alter rock masses and their geometries. These structures contain joints, fractures, bedding planes, shear zones, mechanical breaks, or any other features ranging from microscopic (<1cm, foliation development by metamorphism[5]) to macroscopic scale (>100m, mid-oceanic ridges).[6]
Geological structures are typically elongated, their orientations are often described as "strike". If a rock body is extensively tilted, taking its slope resistivity into account, it may have a high potential to cause rockfalls.[7] The use of LiDAR in the structural analysis allows measuring landform features from a single outcrop scale to a terrestrial scale. Some geological structures measurement and their importance are listed below:
Rock plane orientation measurement and rockfall risk assessment
Rock plane orientations are the natural inclinations that occurred on a rock plane.[8] Some examples of rock planes are bedding planes, fault planes. The planes' orientations are measured by dip and dip direction with a clinometer and compass, where dip represents the maximum inclination of a plane to the horizontal, dip direction is the direction of the intersection line between horizontal and the inclined plane.[9] A stereonet can visualise the distribution of dip and dip directions to analyse the kinematics of a slope.[9]
Kinematics represents the motion of a rock body without external forces that cause them to move. Kinematics analysis concentrates on the possibility of translational failures due to planes sliding.[9]
Faults behaviours measurement and earthquakes predictions
Faults behaviours can be used to measure the rate of sediment transportation and predict earthquakes. An earthquake can contribute to the formation of faults scraps. One side of a block will be relatively upthrown, causing vertical displacements. Therefore, given the parameters of fault scraps, structural geologists are able to trance the age of it and deduce the time involved to form such features.[10]
Earthquakes are initiated by slow slips. Slips are the displaced blocks along two sides of a fault. However, these slips are undetectable by seismometers (maximum 5mm/day).[11] When the slipping blocks reach a critical rupture velocity, the faults would gradually evolve into a final quake size by linear acceleration along fault planes.[11] The critical displacement of faults is proportional to the initial rupture velocities.[12]
After collecting LiDAR data from pre-earthquake and post-earthquake landforms, by constructing 3-D digital terrain models, the displacement and deformations can be derived.[13] Thus, scientists can predict the final earthquake scale in the future by determining faults and slips' characteristics and areas' size, and short-term earthquake predictions are possible.[14]
Surface processes and geological mapping
When carrying out geological mapping, interpretations through aerial photographs and satellite imagery are often used, but forest vegetation remained the major challenge for mapping. For example, characterising physical landform features at ridges and valleys are somehow complicated, many of these features are forest-covered. The topographic maps are then constructed by obtaining data manually.[15]
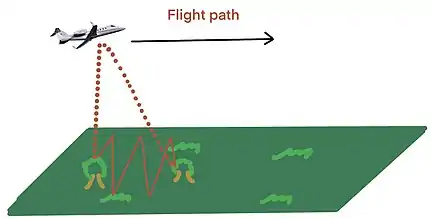
LiDAR provides the full-waveform system, it enables the laser pulse to penetrate through canopies and vegetations.[15] This system allows obtaining bare-ground geological data points. Webster et al. have discovered new craters in Northern Canada by harnessing LiDAR data and digital terrain models. A digital terrain model has to be constructed to measure structural parameters (tilt angles, river incision depths).[16] With the precise bedrock and surficial lithology mapping by LiDAR, structural geologists can reconstruct surficial processes involved.
Traditional structural measurement
Traditional structural orientations can only be assessed on reachable exposed rock mass manually. Conventionally, engineering geologists investigated rock discontinuities studies with only a limited number at a time. The discontinuities may not represent the whole outcrop.[3] Thus, the traditional rock plane orientation measurement may contain bias.
Geotechnical studies also investigate other geomechanical parameters, such as persistence, block size and rock joint spacing.[8]
LiDAR technology
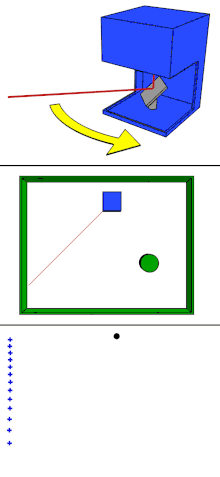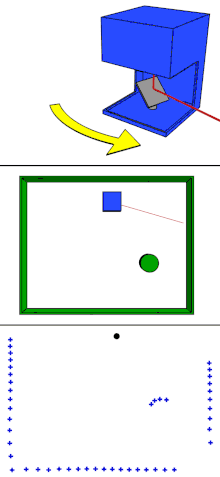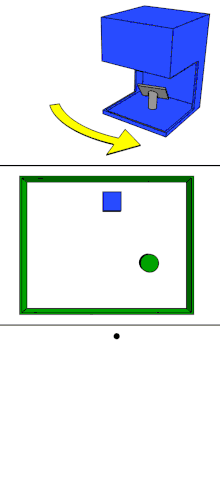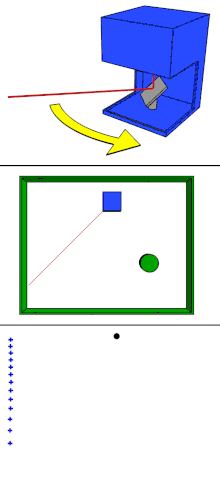
LiDAR (Light Detection and Ranging) is a rapid surveying process that emits and receives laser pluses to acquire 3-D information.[3] By illuminating lights with different wavelengths to the object of interest, LiDAR can be used to create precise topographic maps, with applications in: geology, geomorphology, surveying and other applications.[3] Topographic maps are possible because of the Inertial Measuring Unit and Global Positioning System.[3] Furthermore, it is a technology that can carry out studies on a steep slope and rock-cliffs.[4]
Accurately measured data is necessary for the LiDAR data to be geo-referenced such as locating the data in a local or global coordinates system. Therefore, the produced LiDAR can be overlaid onto the aerial photographs collected previously to observe the topography changes over time.[17]
Principle of LiDAR
LiDAR system emits pulsed and continuous-wave lasers to acquire 3-D information. The laser scanner is the main component of LiDAR. Lasers with a wavelength of 550-600 nm are used on a ground-based system (handheld laser scanning and terrestrial laser scanning), whereas airborne systems use lasers with 1000-1600 nm wavelength.[18]
Laser calculates the reachable range by the following formula:[18]
- R represents Range in meters
- c represents speed of light in m/s
- t is the travelling time of a laser pulser in seconds
LiDAR receives information by discrete and full-waveform return. Full-waveform (multi-return) is often used for forest analysis by Airborne LiDAR, while discrete return (single return) is used by a ground-based laser scanning method.[18] A laser is reflected whenever it reaches any surfaces. The full-waveform return is able to penetrate down into canopies and return vegetation information at different heights.[18] Discrete return can only return the superficial materials.[18] Thus, airborne LiDAR is often used for forestry studies.
Data representation and data format
LiDAR data is mainly stored in a point cloud format(.las). The captured point cloud data store X, Y Z geometric data. Each data point is obtained from a single laser scan and represents a local geo-referenced spatial datum.[19] It can represent realistic and three-dimensional rock faces in a remote and inaccessible natural terrain.[20]
The LiDAR data have the following parameters:
- Each data point contains Co-ordinates (X, Y, Z co-ordinates in a local reference system)[21]
- Each point has its associated color information(R, G, B format)[21]
- The reflected intensity of the surface[19][21]
- Possible automatic superposition of photographs onto point clouds (captured during scanning process)[19]
- Any other hyperspectral data[21]
These data help rock body features analysis, they include recorded geometrical or radiometric information of natural, excavated, or blasted rock slopes.
Previously, the LiDAR data are in the form of the American Standard Code for Information Interchange format(ASCII),[17] which has several problems :
1) Low reading and interpreting speed of ASCII files[17]
2) Useful data loss during data processing[17]
3) ASCII is unstandardised[17]
After 2003, the American Society for Photogrammetry and Remote Sensing (ASPRS) has standardized the LiDAR data in sequential binary laser(.las file) containing LiDAR or other point cloud data records.[17]
Geo-referencing
Geo-referencing means the co-ordinates on an aerial photograph/digital terrain model can be referenced on a global/regional geographic system. Thus, the users are able to determine and locate every point of collected data on the Earth's surface.[17] The typical global positioning system uses the World Geodetic System of 1984(WGS84) datum, and stores the geo-referenced data in GeoTIFF/GeoPDF format.[22] In addition, the users may require orthometric elevation (elevation above sea-level or geoid model) in different scenarios. For example, analysing sea-level change by hydrological data.[17]
Geo-referencing can be done by adding control points at the base of the slope.[8] By shifting the point cloud data onto the known correct co-ordinates with at least 3 points, the point cloud data can be repositioned into an accurate co-ordinate system.[23] This information is useful for calculating distances, volume and areas.
Types of LiDAR
LiDAR data can be collected on ground-based, airborne and mobile platforms. For example, Airborne LiDAR Scanning (ALS), Unmanned Aerial Vehicles (UAV), Terrestrial Laser Scanning (TLS) and Handheld Laser Scanning (HLS). The tables below will compare the mentioned data collection platforms:
1) The data collection methods
2) Geo-referencing technique (how to acquire the exact coordinate of a point)
3) Advantages and disadvantages
| Airborne LiDAR Scanning (ALS) | Unmanned Aerial Vehicle (UAV) | Terrestrial Laser Scanning | Handheld Laser Scanning |
|---|---|---|---|
|

|

|

|
| LiDAR scanning methods | Data collection methods | Geo-referencing technique | Advantages | Disadvantages |
|---|---|---|---|---|
| Airborne LiDAR Scanning (ALS) |
|
|
| |
| Unmanned Aerial Vehicle (UAV) |
|
|
||
| Terrestrial Laser Scanning (TLS) |
|
|
||
| Handheld Laser Scanning (HLS) |
|
Digital terrain modelling
A digital terrain model (DTM) is a mathematical model that represents Earth's visible terrain surfaces.[36] A DTM transforms discernible LiDAR data points into a continuous 3-D surface, the model connects discrete points with distinct height values to form planes. Thus, structural geologists are able to derive structural orientations from these 3-D planes. This modelling technique is also used to create digital planetary surfaces and there are more other applications.[36]
Principle of Digital Terrain Model
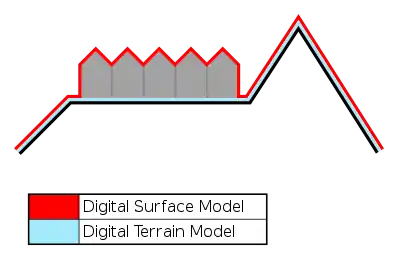
The DTMs are classified by the basic geometric units, such as triangles, squares. 3 major mathematic functions are used, as listed below :
Moreover, triangle-based and grid-based are the most used.
Point-based
Point-based surface modelling reconstructs a surface by forming a series of small contiguous discontinuous surfaces. Each of the surfaces is planar and formed by connecting the individual data point.[25] This function can form a surface with regular and irregular patterns by considering the regional boundaries of influence of each point, where a Voronoi diagram defines the regional boundaries. However, regular patterns are most widely used for simpler computations, such as hexagons, squared patterns.[25]
The mathematical expression of the formation for each horizontal planar-surface is:[16]
where Z is the height of the planar surface, and H is the ith point's height.
Triangular-based
A triangular-based function can form a more tilted or irregular digital surface model. This approach is treated as the primary way to construct a complex DTM. Triangles have great flexibility, any polygons (e.g. a square, rectangle) can be decomposed into other smaller triangles.[20] A linked triangular network can incorporate break lines for plane fitting, it facilitates the formation of a curved facet/surface.[36] The minimum requirement for forming a triangle requires 3 data points, where the nearest 3 points are grouped to form a triangle by Delaunay triangulation without overlapping.[37]
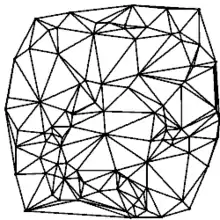
As the data points are unevenly distributed, the triangular-based method effectively constructs DTM because this method can create surface variations. Even some data points of the point cloud are removed or added, a local triangle can be reformed without complete DTM reconstruction.[37]
A few parameters control the surface formation process:
1) Density of Mesh
2) Maximum angle of neighbouring triangles
3) Minimum Patch size
Grid-based
The grid-based model has less relevance for constructing broken terrain or sharp terrain discontinuities with steep slopes.[36] 4 data points are the minimum requirement for forming a grid-based model.[4] The resulting surface is named a bi-linear surface that quadrilaterals of any shapes are linked to create a DTM, such as parallelograms, squares, rectangles or other irregular polygons.[30] This method has the advantage of data handling that the data is in the form of squared grids, evenly distributing data points. In this case, some software has provided a "Random-to-Grid" operation to ensure that the data has the grid form.[37]
Approach for digital terrain modelling
As the data collected are in the form of a point cloud, there is a need to transform these 3-D co-ordinates of laser points into a digital terrain model with 2 major procedures:
1) Point cloud classification and ground filtering
2) Reconstruction of the ground surface from discrete laser point cloud data by interpolation.
Data processing and classification (Airborne LiDAR scanning only)
Data classification and noise cleaning are the processes of obtaining a non-biased slope surface. When ALS collects the with multiple returns, this principle can classify the objects into different categories. Classification algorithms can be performed by TerraScan & TerraModel, computer software for classifying point cloud data automatically developed by TerraSolid.[38] However, some manual adjustments and validations are needed to ensure the data points are classified correctly.
Algorithms can identify pre-dominate landform features, these algorithms assume the surfaces with significant variations are non-ground features.[30] For creating a surface model of rock slope, only classified ground data is needed. The classifications of the ground and non-ground surfaces are in the following categories:
| Classifications | Examples |
|---|---|
| Flat, ground or open terrain | Open terrain, sand, rock, flat rooftops, golf courses[25] |
| Low-vegetation area | Tall crops and weeds <2m[25] |
| Medium-vegetation area | Low trees or brushlands between 2 and 10m[25] |
| High-vegetation area | Forested areas >10m[25] |
Data filtering
Data filtering enables the extraction of bare-Earth's surface by removing unnecessary data or data noise.[25] For rock orientation studies, outcrop mapping and topographical studies, they only acquire information about the rock slope bodies. Thus, data filtering is implemented to separate the point clouds as ground and non-ground features. Bugs, vegetations or other artificial infrastructures belong to non-ground features.[39]
In order to filter 3-D laser points, few methods from open source software can be applied to filter ground points out of the whole area of interests :
| Author | Technique | Description of the method | Accuracy |
|---|---|---|---|
| Axelsson et al., 2000[40] | Triangular-irregular network (TIN) | Multiple points are divided into grids. The lower elevation within each grid is treated as ground points. Users can set the grid size on their own. The points are added into a triangle facet when they are close enough. | Satisfactory |
| Zeybek, 2019 | Cloth-simulation method | A simulated cloth is put on the up-side-down point cloud, points are not filtered when the cloth can touch the data points. The softer the cloth, the more intersection points can be preserved. The intersected points are then classified as a ground.[33] | 93% |
| Surface-based | This method uses a linear algorithm to remove the non-ground points[33] | 81% | |
| Curvature based | Fitting is applied to the nearest neighbour, the points with large elevation variations(Z component) are filtered out.[33] | 88% |
Ground verification survey
The purpose of the ground verification survey is to test the accuracy of LiDAR. LiDAR data is acquired by sending laser pulses at different angles or receiving the returning signal, these signals may include some error induced by atmosphere absorption of wavelength.[41] Therefore, a ground-truth survey is needed to ensure the collected data's co-ordinates match the local coordinate system. For example, horizontal accuracy will be tested by comparing the collected data through different data collection techniques. Also, data can be corrected by setting multiple control points with known coordinates.[42]
Structural orientation analysis
The DTMs are capable of identifying the structural parameters of geological features(tilt angle of a fold limb). For example, dip and dip directions of rock planes can be derived from DTM. The general methodology has the following steps:
1) Obtain LiDAR data of a targeted slope[26]
2) Noise cleaning and filtering of point data[26]
3) Transform point data into DTM through mathematical functions[8]
4) By using programs, such as Coltop 3D, the structural geometry of the joint/slope planes can be calculated automatically.[8]
5) The rock planes are determined by color-coding or statistical method for evaluating whether the points are grouped to form a single or different planes.[8][26]
6) Output the structural orientations data into suitable computer software files, and plotting the distribution of dip and dip directions of different planes on a stereonet.[8][26]
Data partition
Data partitioning helps redistribute the unevenly distributed point data by dividing data into cubes. Returned point cloud data has different point density, due to the variation of data collection devices and parameters. The point cloud's density determines the cube size, no fewer than 4 points form each cube.[43] The points that are considered as non-conformers will be removed from the point cloud.[43] Afterwards, the normal vector of each cube will be calculated.
Octree Partitioning in open source softwares, including CloudCompare and Geomagic, can achieve data partitioning.[43] Considering the rock masses in different terrains, they have variations in the roughness. Thus, it is necessary for users to set the cube size manually to obtain the best cube. The average number of points in each cube ranges from 15 to 30 points, by setting the range of the point spacing between 4mm and 7mm.[43]
Cluster analysis by normal vectors
The purpose of rock discontinuities clustering is to group sub-planes of a slope into the same discontinuity set they belong to. The discontinuities demonstrate waviness, roughness or an undulating surface.[43] The points within the same joint set show similar orientation habits.[43] The algorithm determines whether the points are located within the main orientation of bedding planes or sub-parallel planes with each other.[44] The clustering technique can classify different joint sets based on assigned normal vectors on each face within approximately the same orientation.[44]
Challenges for LiDAR Technology
Although LiDAR has high efficiency in collecting data in a large area within a short time, some issues remain challenging for the overall data processing and generating the expected result.
Data filtering and surface generation parameters

Vegetation may not be entirely removed during data filtering. It may affect the smoothness and the clustering of rock surfaces. In most cases, 3-D models are generated through the triangulation method, spikes are often formed.[18] The spikes may affect the clustering of rock surfaces. They affect the smoothness of the 3-D surface, inducing errors in calculating the rock plane orientations. Spikes are formed when the data points have similar X and Y coordinates but very different Z coordinates, the needle-like shape triangles are produced as a result of non-smooth surfaces.[45]
The filtering parameters for surface clustering often depend on users' past experiences. For example, the octree parameter can be adjusted with different point densities.[17] The result of DTM formation has to be determined by users. Hence, a repeated testing procedure is needed for generating a satisfactory surface.[25]
Point density
Point cloud density, known as the spacing between each data point in an obtained LiDAR datasets.[45] This parameter affects the accuracy in measuring rock slopes. It is one of the characteristics that need to be considered during data processing. For example, data filtering, classification, feature extraction and object recognition.[34] Point cloud density depends on various factors:
Cost
Although LiDAR has been an effective data acquisition method on a rock slope, its high cost caused the technique to be not practical.[47] When the area of interest is of a very small scale, it limits the usability of TLS & ALS, given carrying out an ALS survey requires aircraft, an experienced pilot, a designed flying path and height that got the approval of the local aviation department.[29]
By employing UAV, the problem mentioned above can be resolved. It can collect data in inaccessible areas that enable data collection at a low cost at a small scale, since the device is portable and lightweight.[33]
Other LiDAR applications
With the high accuracy and high-efficiency data acquisition method of laser scanning, it can potentially apply to different areas other than structural measurements:
- Emergency inspections and landslide mapping[47]
- Project management (with the need of 3-D models / topographic data)[47]
- Site progress, the volume of excavation or filling[47]
- Volumetric calculations[41]
- Topographic mapping[41]
- Building and highway construction[41]
- Natural disasters assessments[27]
- Unreachable area data collection[48]
- Precision farming[48]
- As-built construction records[48]
- Unauthorised works (e.g. capturing of field situation)[48]
- Monitoring surface deformation with continuous and repeated LiDAR scanning[48]
- Archaeology and site reconstructions[24]
- Seismology[24]
- Forestry[24]
- Atmospheric physics [24]
- Extraterrestrial explorations[24]
References
- Abellán, Antonio; Oppikofer, Thierry; Jaboyedoff, Michel; Rosser, Nicholas J.; Lim, Michael; Lato, Matthew J. (2013-11-13). "Terrestrial laser scanning of rock slope instabilities". Earth Surface Processes and Landforms. 39 (1): 80–97. doi:10.1002/esp.3493. ISSN 0197-9337.
- Akturk, Emre; Altunel, Arif Oguz (2018-12-31). "Accuracy assessment of a low-cost UAV derived digital elevation model (DEM) in a highly broken and vegetated terrain". Measurement. 136: 382–386. doi:10.1016/j.measurement.2018.12.101. ISSN 0263-2241.
- Sturzenegger, Matthieu; Willms, David; Pate, Kimberley; Johnston, Brent (2013). "Experience using terrestrial remote sensing techniques for rock slope performance assessment". Proceedings of the 2013 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering. Australian Centre for Geomechanics, Perth: 775–782. doi:10.36487/acg_rep/1308_52_sturzenegger. ISBN 978-0-9870937-5-2.
- HESS, MONA, "3D LASER SCANNING", Digital Techniques for Documenting and Preserving Cultural Heritage, Arc Humanities Press, pp. 199–206, doi:10.2307/j.ctt1xp3w16.19, ISBN 978-1-942401-35-3, retrieved 2020-10-06
- Hickey, Ken A.; Bell, Tim H. (1997-01-08). "Syn-deformational grain growth: matrix coarsening during foliation development and regional metamorphism rather than by static annealing". European Journal of Mineralogy. 8 (6): 1351–1374. doi:10.1127/ejm/8/6/1351. ISSN 0935-1221.
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J. M. (2009-03-17). "Detection of millimetric deformation using a terrestrial laser scanner: experiment and application to a rockfall event". Natural Hazards and Earth System Sciences. 9 (2): 365–372. Bibcode:2009NHESS...9..365A. doi:10.5194/nhess-9-365-2009. ISSN 1684-9981.
- "Principles of Electric Methods in Surface and Borehole Geophysics". Methods in Geochemistry and Geophysics. 2010. doi:10.1016/c2009-0-16239-6. ISSN 0076-6895.
- Riquelme, Adrián; Tomás, Roberto; Cano, Miguel; Pastor, José Luis; Abellán, Antonio (2018-05-24). "Automatic Mapping of Discontinuity Persistence on Rock Masses Using 3D Point Clouds". Rock Mechanics and Rock Engineering. 51 (10): 3005–3028. Bibcode:2018RMRE...51.3005R. doi:10.1007/s00603-018-1519-9. ISSN 0723-2632. S2CID 135109573.
- Mathis, James (2007). "Pit Slope Design and Structural Analysis at the Jericho Diamond Mine Utilising Digital Photogrammetric Mapping". Proceedings of the 2007 International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering. Australian Centre for Geomechanics, Perth: 93–104. doi:10.36487/acg_repo/708_4. ISBN 978-0-9756756-8-7.
- "Fault scarp, fault-line scarp", SpringerReference, Berlin/Heidelberg: Springer-Verlag, retrieved 2020-12-15
- Abercrombie, Rachel E. (2019-09-04). "Small and large earthquakes can have similar starts". Nature. 573 (7772): 42–43. doi:10.1038/d41586-019-02613-5. ISSN 0028-0836.
- Ellsworth, W. L.; Beroza, G. C. (1995-05-12). "Seismic Evidence for an Earthquake Nucleation Phase". Science. 268 (5212): 851–855. doi:10.1126/science.268.5212.851. ISSN 0036-8075.
- Francesco Silvestri; Nicola Moraci (22 October 2019). Earthquake Geotechnical Engineering for Protection and Development of Environment and Constructions: Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, (ICEGE 2019), June 17-20, 2019, Rome, Italy. CRC Press. p. 496. ISBN 978-0-429-63350-8.
- Richard C. Berg (2011). Synopsis of Current Three-dimensional Geological Mapping and Modeling in Geological Survey Organizations. Illinois State Geological Survey. p. 73.
- "Microscanning of Lidar Images for Improved Sampling", Field Guide to Lidar, SPIE PRESS, ISBN 978-1-62841-654-1, retrieved 2020-12-15
- Webster, Tim L; Murphy, J. Brendan; Gosse, John C; Spooner, Ian (2006). "The application of lidar-derived digital elevation model analysis to geological mapping: an example from the Fundy Basin, Nova Scotia, Canada". Canadian Journal of Remote Sensing. 32 (2): 173–193. doi:10.5589/m06-017. ISSN 0703-8992.
- Guo, Jiateng; Liu, Shanjun; Zhang, Peina; Wu, Lixin; Zhou, Wenhui; Yu, Yinan (2017-03-24). "Towards semi-automatic rock mass discontinuity orientation and set analysis from 3D point clouds". Computers & Geosciences. 103: 164–172. Bibcode:2017CG....103..164G. doi:10.1016/j.cageo.2017.03.017. ISSN 0098-3004.
- Dong, Pinliang; Chen, Qi (2017-12-12), "Basics of LiDAR Data Processing", LiDAR Remote Sensing and Applications, Boca Raton, FL : Taylor & Francis, 2018.: CRC Press, pp. 41–62, doi:10.4324/9781351233354-3, ISBN 978-1-351-23335-4, retrieved 2020-10-07CS1 maint: location (link)
- Campbell, Michael J.; Dennison, Philip E.; Butler, Bret W. (2017). "A LiDAR-based analysis of the effects of slope, vegetation density, and ground surface roughness on travel rates for wildland firefighter escape route mapping". International Journal of Wildland Fire. 26 (10): 884. doi:10.1071/wf17031. ISSN 1049-8001.
- Zhou, Cuiying; Du, Zichun; Ouyang, Jinwu; Zhang, Zhilong; Liu, Zhen (2020). "A 3D geological model and cutting algorithm based on a vertically projected triangulated network". Computers & Geosciences. 143: 104562. Bibcode:2020CG....14304562Z. doi:10.1016/j.cageo.2020.104562. ISSN 0098-3004.
- Burton, D.; Dunlap, D. B.; Wood, L. J.; Flaig, P. P. (2011-05-01). "Lidar Intensity as a Remote Sensor of Rock Properties". Journal of Sedimentary Research. 81 (5): 339–347. Bibcode:2011JSedR..81..339B. doi:10.2110/jsr.2011.31. ISSN 1527-1404.
- González-Jorge, Higinio; Arias, Pedro; Puente, Iván; Martínez, Joaquín (2012-06-29). "Surveying of Road Slopes Using Mobile LiDAR". ISG*ISARC2012 Full Paper Proceedings. International Association for Automation and Robotics in Construction (IAARC). doi:10.22260/isarc2012/0015. ISBN 978-90-386-3410-4.
- Jordá Bordehore, Luis; Riquelme, Adrian; Cano, Miguel; Tomás, Roberto (2017-06-24). "Comparing manual and remote sensing field discontinuity collection used in kinematic stability assessment of failed rock slopes". International Journal of Rock Mechanics and Mining Sciences. 97: 24–32. doi:10.1016/j.ijrmms.2017.06.004. hdl:10045/67528. ISSN 1365-1609.
- Okyay, Unal; Telling, Jennifer; Glennie, Craig L.; Dietrich, William E. (November 2019). "Airborne lidar change detection: An overview of Earth sciences applications". Earth-Science Reviews. 198: 102929. Bibcode:2019ESRv..19802929O. doi:10.1016/j.earscirev.2019.102929. ISSN 0012-8252.
- Advances in Airborne Lidar Systems and Data Processing. 2018-05-11. doi:10.3390/books978-3-03842-674-5. ISBN 978-3-03842-674-5.
- Farmakis, Ioannis Verfasser. Automated 3D Jointed Rock Mass Structural Analysis and Characterization Using LiDAR Terrestrial Laser Scanner for Rockfall Susceptibility Assessment: Perissa Area Case (Santorini). OCLC 1196463534.
- Pradhan, Biswajeet; Yusof, Norbazlan Mohd (2017), "Slope Vulnerability and Risk Assessment Using High-Resolution Airborne Laser Scanning Data", Laser Scanning Applications in Landslide Assessment, Cham: Springer International Publishing, pp. 235–251, doi:10.1007/978-3-319-55342-9_12, ISBN 978-3-319-55341-2, retrieved 2020-10-08
- Wu, Zhuoting; Dye, Dennis; Stoker, Jason; Vogel, John; Velasco, Miguel; Middleton, Barry (2016-02-09). "Evaluating Lidar Point Densities for Effective Estimation of Aboveground Biomass". International Journal of Advanced Remote Sensing and GIS. 5 (1): 1483–1499. doi:10.23953/cloud.ijarsg.40. ISSN 2320-0243.
- McGaughey, W (2019). "Data-driven geotechnical hazard assessment: practice and pitfalls". Proceedings of the First International Conference on Mining Geomechanical Risk. Australian Centre for Geomechanics, Perth: 219–232. doi:10.36487/acg_rep/1905_11_mcgaughey. ISBN 978-0-9876389-1-5.
- Guo, Jiateng; Liu, Shanjun; Zhang, Peina; Wu, Lixin; Zhou, Wenhui; Yu, Yinan (2017). "Towards semi-automatic rock mass discontinuity orientation and set analysis from 3D point clouds". Computers & Geosciences. 103: 164–172. Bibcode:2017CG....103..164G. doi:10.1016/j.cageo.2017.03.017. ISSN 0098-3004.
- Pradhan, Biswajeet. Buchroithner, Manfred F. (2012). Terrigenous mass movements : detection, modelling, early warning and mitigation using geoinformation technology. Springer. ISBN 978-3-642-25495-6. OCLC 785560465.CS1 maint: multiple names: authors list (link)
- Pradhan, Biswajeet; Sameen, Maher Ibrahim (2017), "Laser Scanning Systems in Landslide Studies", Laser Scanning Applications in Landslide Assessment, Cham: Springer International Publishing, pp. 3–19, doi:10.1007/978-3-319-55342-9_1, ISBN 978-3-319-55341-2, retrieved 2020-10-07
- Zeybek, Mustafa; Şanlıoğlu, İsmail (2018-10-07). "Point cloud filtering on UAV based point cloud". Measurement. 133: 99–111. doi:10.1016/j.measurement.2018.10.013. ISSN 0263-2241.
- Bauwens, Sébastien; Bartholomeus, Harm; Calders, Kim; Lejeune, Philippe (2016-06-21). "Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning". Forests. 7 (12): 127. doi:10.3390/f7060127. ISSN 1999-4907.
- Lee, Yong Wook (2013-04-30). "Decision Of EO Parameters Based On Direct Georeferencing Using SmartBase". Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography. 31 (2): 135–142. doi:10.7848/ksgpc.2013.31.2.135. ISSN 1598-4850.
- "Generation of digital terrain and surface models", Digital Photogrammetry, Abingdon, UK: Taylor & Francis, pp. 159–299, 2002, doi:10.4324/9780203305959_chapter_3, ISBN 978-0-203-35360-8, retrieved 2020-11-13
- "Terrain Modeling Software and Services", Environmental Applications of Digital Terrain Modeling, Chichester, UK: John Wiley & Sons, Ltd, pp. 228–260, 2018-02-16, doi:10.1002/9781118938188.ch6, ISBN 978-1-118-93818-8, retrieved 2020-10-08
- Tam, Chung-yan, Candy. Study of rock joint roughness using 3D laser scanning technique (Thesis). The University of Hong Kong Libraries. doi:10.5353/th_b4020348.
- Richman, A.; Hamilton, A.; Arayici, Y.; Counsell, J.; Tkhelidze, B. (2005). "Remote Sensing, LIDAR, Automated Data Capture and the VEPS Project". Ninth International Conference on Information Visualisation (IV'05). IEEE: 151–156. doi:10.1109/iv.2005.106. ISBN 0-7695-2397-8. S2CID 15794226.
- Axelsson, P. (2000). "DEM Generation from Laser Scanner Data Using Adaptive TIN Models". CiNii. International Archives of Photogrammetry and Remote Sensing. Retrieved December 27, 2020.
- Jones, L. D. (2006). Monitoring landslides in hazardous terrain using terrestrial LiDAR : an example from Montserrat. OCLC 770329355.
- Gordon, Stuart J.; Lichti, Derek D. (2007). "Modeling Terrestrial Laser Scanner Data for Precise Structural Deformation Measurement". Journal of Surveying Engineering. 133 (2): 72–80. doi:10.1061/(asce)0733-9453(2007)133:2(72). ISSN 0733-9453.
- Han, Soohee (2018-12-12). "Towards Efficient Implementation of an Octree for a Large 3D Point Cloud". Sensors. 18 (12): 4398. doi:10.3390/s18124398. ISSN 1424-8220. PMC 6308722. PMID 30545103.
- Jaboyedoff, Michel; Abellán, Antonio; Carrea, Dario; Derron, Marc-Henri; Matasci, Battista; Michoud, Clément (2018-03-22), "Mapping and Monitoring of Landslides Using LIDAR", Natural Hazards, Boca Raton, Florida : Taylor & Francis, 2018. | "A CRC title, part of the Taylor & Francis imprint, a member of the Taylor & Francis Group, the academic division of T&F Informa plc.": CRC Press, pp. 397–420, doi:10.1201/9781315166841-17, ISBN 978-1-315-16684-1, retrieved 2020-10-07CS1 maint: location (link)
- Khosravipour, Anahita; Skidmore, Andrew K.; Isenburg, Martin (2016). "Generating spike-free digital surface models using LiDAR raw point clouds: A new approach for forestry applications". International Journal of Applied Earth Observation and Geoinformation. 52: 104–114. Bibcode:2016IJAEO..52..104K. doi:10.1016/j.jag.2016.06.005. ISSN 0303-2434.
- Luo, Shezhou; Chen, Jing M.; Wang, Cheng; Xi, Xiaohuan; Zeng, Hongcheng; Peng, Dailiang; Li, Dong (2016-05-18). "Effects of LiDAR point density, sampling size and height threshold on estimation accuracy of crop biophysical parameters". Optics Express. 24 (11): 11578–93. Bibcode:2016OExpr..2411578L. doi:10.1364/oe.24.011578. ISSN 1094-4087. PMID 27410085.
- Collins, Brian D.; Stock, Greg M. (2012-03-29). "Lidar-Based Rock-Fall Hazard Characterization of Cliffs". GeoCongress 2012. Reston, VA: American Society of Civil Engineers: 3021–3030. doi:10.1061/9780784412121.309. ISBN 978-0-7844-1212-1.
- Kennedy, Michael (2009-07-07). The Global Positioning System and ArcGIS. doi:10.1201/9781420088007. ISBN 9780429144547.
External links
For more detailed description of the concepts, some links are provided below: