Glossary of module theory

Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.

A

algebraically compact: algebraically compact module (also called pure injective module) is a module in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.
annihilator: 1. The annihilator of a left $R$ -module $M$ is the set ${\textrm {Ann}}(M):=\{r\in R|rm=0\,\forall m\in M\}$ . It is a (left) ideal of $R$ .; 2. The annihilator of an element $m\in M$ is the set ${\textrm {Ann}}(m):=\{r\in R|rm=0\}$ .
Artinian: An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.
associated prime: 1. An associated prime.
Azumaya: Azumaya's theorem says that two decompositions into modules with local endomorphism rings are equivalent.

B

balanced: balanced module
basis: A basis of a module $M$ is a set of elements in $M$ such that every element in the module can be expressed as a finite sum of elements in the basis in a unique way.
Beauville–Laszlo: Beauville–Laszlo theorem
bimdule: bimodule

C

character: character module
coherent: A coherent module is a finitely generated module whose finitely generated submodules are finitely presented.
completely reducible: Synonymous to "semisimple module".
composition: Jordan Hölder composition series
continuous: continuous module
cyclic: A module is called a cyclic module if it is generated by one element.

D

D: A D-module is a module over a ring of differential operators.
dense: dense submodule
direct sum: A direct sum of modules is a module that is the direct sum of the underlying abelian group together with component-wise scalar multiplication.
dual module: The dual module of a module M over a commutative ring R is the module $\operatorname {Hom} _{R}(M,R)$ .
Drinfeld: A Drinfeld module is a module over a ring of functions on algebraic curve with coefficients from a finite field.

E

Eilenberg–Mazur: Eilenberg–Mazur swindle
elementary: elementary divisor
endomorphism: The endomorphism ring.
essential: Given a module M, an essential submodule N of M is a submodule that every nonzero submodule of M intersects non-trivially.
Ext functor: Ext functor.
extension: Extension of scalars uses a ring homomorphism from R to S to convert R-modules to S-modules.

F

faithful: A faithful module $M$ is one where the action of each nonzero $r\in R$ on $M$ is nontrivial (i.e. $rx\neq 0$ for some $x$ in $M$ ). Equivalently, ${\textrm {Ann}}(M)$ is the zero ideal.
finite: The term "finite module" is another name for a finitely generated module.
finite length: A module of finite length is a module that admits a (finite) composition series.
finite presentation: 1. A finite free presentation of a module M is an exact sequence $F_{1}\to F_{0}\to M$ where $F_{i}$ are finitely generated free modules.; 2. A finitely presented module is a module that admits a finite free presentation.
finitely generated: A module $M$ is finitely generated if there exist finitely many elements $x_{1},...,x_{n}$ in $M$ such that every element of $M$ is a finite linear combination of those elements with coefficients from the scalar ring $R$ .
fitting: fitting ideal
five: Five lemma.
flat: A $R$ -module $F$ is called a flat module if the tensor product functor $-\otimes _{R}F$ is exact.
In particular, every projective module is flat.
free: A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring $R$ .

G

Galois: A Galois module is a module over the group ring of a Galois group.

H

graded: A module $M$ over a graded ring $A=\bigoplus _{n\in \mathbb {N} }A_{n}$ is a graded module if $M$ can be expressed as a direct sum $\bigoplus _{i\in \mathbb {N} }M_{i}$ and $A_{i}M_{j}\subseteq M_{i+j}$ .
homomorphism: For two left $R$ -modules $M_{1},M_{2}$ , a group homomorphism $\phi :M_{1}\to M_{2}$ is called homomorphism of $R$ -modules if $r\phi (m)=\phi (rm)\,\forall r\in R,m\in M_{1}$ .
Hom: Hom functor.

I

indecomposable

An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable (but not conversely).

injective

1. A

R

-module

Q

is called an injective module if given a

R

-module homomorphism

g:X\to Q

, and an injective

R

-module homomorphism

f:X\to Y

, there exists a

R

-module homomorphism

h:Y\to Q

such that

f\circ h=g

.

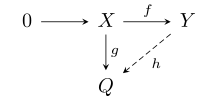The module Q is injective if the diagram commutes

The following conditions are equivalent:

The contravariant functor ${\textrm {Hom}}_{R}(-,I)$ is exact.
$I$ is a injective module.
Every short exact sequence $0\to I\to L\to L'\to 0$ is split.

2. An injective envelope is a maximal essential extension, or a minimal embedding in an injective module.

3. An injective cogenerator is an injective module such that every module has a nonzero homomorphism into it.

invariant

invariants

invertible

An invertible module over a commutative ring is a rank-one finite projective module.

irreducible module

Another name for a simple module.

J

Jacobson: density theorem

K

Kaplansky: Kaplansky's theorem on a projective module says that a projective module over a local ring is free.
Krull–Schmidt: The Krull–Schmidt theorem says that (1) a finite-length module admits an indecomposable decomposition and (2) any two indecomposable decompositions of it are equivalent.

L

length: The length of a module is the common length of any composition series of the module; the length is infinite if there is no composition series. Over a field, the length is more commonly known as the dimension.
localization: Localization of a module converts R modules to S modules, where S is a localization of R.

M

Mitchell's embedding theorem

Mitchell's embedding theorem

Mittag-Leffler

Mittag-Leffler condition (ML)

module

1. A left module

M

over the ring

R

is an abelian group

(M,+)

with an operation

R\times M\to M

(called scalar multipliction) satisfies the following condition:

\forall r,s\in R,m,n\in M

,

$r(m+n)=rm+rn$
$r(sm)=(rs)m$
$1_{R}\,m=m$

2. A right module

M

over the ring

R

is an abelian group

(M,+)

with an operation

M\times R\to M

satisfies the following condition:

\forall r,s\in R,m,n\in M

,

$(m+n)r=mr+nr$
$(ms)r=r(sm)$
$m1_{R}=m$

3. All the modules together with all the module homomorphisms between them form the category of modules.

N

Noetherian: A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.
normal: normal forms for matrices

P

principal

A principal indecomposable module is a cyclic indecomposable projective module.

primary

A primary submodule

projective

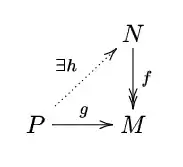The characteristic property of projective modules is called lifting.

A

R

-module

P

is called a projective module if given a

R

-module homomorphism

g:P\to M

, and a surjective

R

-module homomorphism

f:N\to M

, there exists a

R

-module homomorphism

h:P\to N

such that

f\circ h=g

.

The following conditions are equivalent:

The covariant functor ${\textrm {Hom}}_{R}(P,-)$ is exact.
$M$ is a projective module.
Every short exact sequence $0\to L\to L'\to P\to 0$ is split.
$M$ is a direct summand of free modules.

In particular, every free module is projective.

2. The projective dimension of a module is the minimal length of (if any) a finite projective resolution of the module; the dimension is infinite if there is no finite projective resolution.

3. A projective cover is a minimal surjection from a projective module.

Q

quotient: Given a left $R$ -module $M$ and a submodule $N$ , the quotient group $M/N$ can be made to be a left $R$ -module by $r(m+N)=rm+N$ for $r\in R,\,m\in M$ . It is called a quotient module or factor module.

R

radical: The radical of a module is the intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.
rational: rational canonical form
reflexive: A reflexive module is a module that is isomorphic via the natural map to its second dual.
resolution: resolution
restriction: Restriction of scalars uses a ring homomorphism from R to S to convert S-modules to R-modules.

S

Schanuel: Schanuel's lemma
snake: Snake lemma
socle: The socle is the largest semisimple submodule.
semisimple: A semisimple module is a direct sum of simple modules.
simple: A simple module is a nonzero module whose only submodules are zero and itself.
stably free: A stably free module
structure theorem: The structure theorem for finitely generated modules over a principal ideal domain says that a finitely generated modules over PIDs are finite direct sums of primary cyclic modules.
submodule: Given a $R$ -module $M$ , an additive subgroup $N$ of $M$ is a submodule if $RN\subset N$ .
support: The support of a module over a commutative ring is the set of prime ideals at which the localizations of the module are nonzero.

T

tensor: Tensor product of modules
Tor: Tor functor.
torsionless: A torsionless module.

U

uniform: A uniform module is a module in which every two non-zero submodules have a non-zero intersection.

References

John A. Beachy (1999). Introductory Lectures on Rings and Modules (1st ed.). Addison-Wesley. ISBN 0-521-64407-0.
Golan, Jonathan S.; Head, Tom (1991), Modules and the structure of rings, Monographs and Textbooks in Pure and Applied Mathematics, 147, Marcel Dekker, ISBN 978-0-8247-8555-0, MR 1201818
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294
Serge Lang (1993). Algebra (3rd ed.). Addison-Wesley. ISBN 0-201-55540-9.
Passman, Donald S. (1991), A course in ring theory, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-13776-2, MR 1096302

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.