Great disnub dirhombidodecahedron
In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a degenerate uniform star polyhedron.
| Great disnub dirhombidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 204, E = 360 V = 60 (χ = −96) |
| Faces by sides | 120{3}+60{4}+24{5/2} |
| Wythoff symbol | | (3/2) 5/3 (3) 5/2 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U-, C-, W- |
| Dual polyhedron | Great disnub dirhombidodecacron |
| Vertex figure |  (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/2 |
| Bowers acronym | Gidisdrid |

It was proven in 1970 that there are only 75 uniform polyhedra other than the infinite families of prisms and antiprisms. John Skilling discovered another degenerate example, the great disnub dirhombidodecahedron, by relaxing the condition that edges must be single. More precisely, he allowed any even amount of faces to meet at each edge, as long as the set of faces couldn't be separated into two connected sets (Skilling, 1975). Due to its geometric realization having some double edges where 4 faces meet, it's considered a degenerate uniform polyhedron but not strictly a uniform polyhedron.
The number of edges is ambiguous, because the underlying abstract polyhedron has 360 edges, but 120 pairs of these have the same image in the geometric realization, so that the geometric realization has 120 single edges and 120 double edges where 4 faces meet, for a total of 240 edges. The Euler characteristic of the abstract polyhedron is −96. If the pairs of coinciding edges in the geometric realization are considered to be single edges, then it has only 240 edges and Euler characteristic 24.
The vertex figure has 4 square faces passing through the center of the model.
It may be constructed as the exclusive or (blend) of the great dirhombicosidodecahedron and compound of twenty octahedra.
Related polyhedra
It shares the same edge arrangement as the great dirhombicosidodecahedron, but has a different set of triangular faces. The vertices and edges are also shared with the uniform compounds of twenty octahedra or twenty tetrahemihexahedra. 180 of the edges are shared with the great snub dodecicosidodecahedron.
 Convex hull |
 Great snub dodecicosidodecahedron |
 Great dirhombicosidodecahedron |
 Great disnub dirhombidodecahedron |
 Compound of twenty octahedra |
 Compound of twenty tetrahemihexahedra |
Dual polyhedron
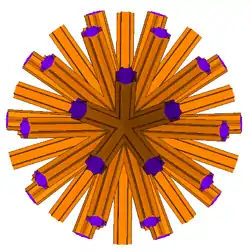
The dual of the great disnub dirhombidodecahedron is called the great disnub dirhombidodecacron. It is a nonconvex infinite isohedral polyhedron.
Like the visually identical great dirhombicosidodecacron in Magnus Wenninger's Dual Models, it is represented with intersecting infinite prisms passing through the model center, cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation polyhedra, called stellation to infinity. However, he also acknowledged that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
Gallery
 Traditional filling |
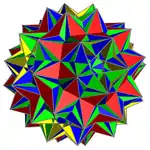 Modulo-2 filling |
See also
References
- Skilling, John (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society A, 278 (1278): 111–135, doi:10.1098/rsta.1975.0022.
- Weisstein, Eric W. "Great dirhombicosidodecahedron". MathWorld.
- http://www.software3d.com/MillersMonster.php