Hysteretic model

Hysteretic models are mathematical models capable of simulating the complex nonlinear behavior characterizing mechanical systems and materials used in different fields of engineering, such as aerospace, civil, and mechanical engineering. Some examples of mechanical systems and materials having a hysteretic behavior are:

materials, such as steel, reinforced concrete, wood;
structural elements, such as steel, reinforced concrete, or wood joints;
devices, such as seismic isolators[1] and dampers.

Hysteretic models may have a generalized displacement $u$ as input variable and a generalized force $f$ as output variable, or vice versa. In particular, in rate-independent hysteretic models, the output variable does not depend on the rate of variation of the input one.[2][3]

Rate-independent hysteretic models can be classified into four different categories depending on the type of equation that needs to be solved to compute the output variable:

Algebraic models
Transcendental models
Differential models
Integral models

Algebraic models

In algebraic models, the output variable is computed by solving algebraic equations.

Model formulation

In the bilinear model formulated by Vaiana et al. (2018),[4] the generalized force at time t, representing the output variable, is evaluated as a function of the generalized displacement as follows:

 $f_{t}=k_{a}\left(u_{t}-u_{j}\right)+k_{b}u_{j}+s_{t}f_{0}{\text{ when }}u_{t}s_{t}<u_{j}s_{t},$

 $f_{t}=k_{b}u_{j}+s_{t}f_{0}{\text{ when }}u_{t}s_{t}>u_{j}s_{t},$

where $k_{a},k_{b},$ and $f_{0}$ are the three model parameters to be calibrated from experimental or numerical tests, whereas $s_{t}$ is the sign of the generalized velocity at time $t$ , that is, $s_{t}=\operatorname {sign} ({\dot {u}}_{t})$ . Furthermore, $u_{0}$ is an internal model parameter evaluated as:

 $u_{0}={\frac {f_{0}}{k_{a}-k_{b}}},$

whereas $u_{j}$ is the history variable:

 $u_{j}={\frac {k_{a}u_{t-\Delta t}+s_{t}f_{0}-f_{t-\Delta t}}{k_{a}-k_{b}}}$ .

Hysteresis loop shapes

Figure 1.1 shows two different hysteresis loop shapes obtained by applying a sinusoidal generalized displacement having unit amplitude and frequency and simulated by adopting the Bilinear Model (BM) parameters listed in Table 1.1.

Figure 1.1. Hysteresis Loops reproduced by using the BM model parameters in Table 1.1

Table 1.1 - BM parameters
	$k_{a}$	$k_{b}$	$f_{0}$
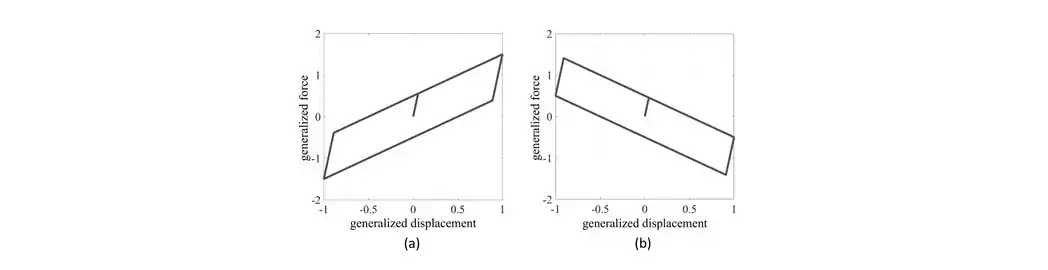
(a)	10.0	1.0	0.5
(b)	10.0	-1.0	0.5

Matlab code

%  =========================================================================================
%  June 2020
%  Bilinear Model Algorithm
%  Nicolò Vaiana, Research Fellow in Structural Mechanics and Dynamics, PhD 
%  Department of Structures for Engineering and Architecture 
%  University of Naples Federico II
%  via Claudio, 21 - 80124, Napoli
%  =========================================================================================

clc; clear all; close all;

%% APPLIED DISPLACEMENT TIME HISTORY

dt = 0.001;                                                                %time step
t  = 0:dt:1.50;                                                            %time interval
a0 = 1;                                                                    %applied displacement amplitude
fr = 1;                                                                    %applied displacement frequency
u  = a0*sin((2*pi*fr)*t(1:length(t)));                                     %applied displacement vector
v  = 2*pi*fr*a0*cos((2*pi*fr)*t(1:length(t)));                             %applied velocity vector
n  = length(u);                                                            %applied displacement vector length

%% 1. INITIAL SETTINGS
%1.1 Set the five model parameters
ka = 10.0;                                                                 %model parameter
kb = 1.0;                                                                  %model parameter
f0 = 0.5;                                                                  %model parameter
%1.2 Compute the internal model parameters 
u0 = f0/(ka-kb);                                                           %internal model parameter
%1.3 Initialize the generalized force vector
f  = zeros(1,n);

%% 2. CALCULATIONS AT EACH TIME STEP

for i = 2:n
%2.1 Update the history variable
uj = (ka*u(i-1)+sign(v(i))*f0-f(i-1))/(ka-kb);
%2.2 Evaluate the generalized force at time t
if (sign(v(i))*uj)-2*u0 < sign(v(i))*u(i) && sign(v(i))*u(i) < sign(v(i))*uj
    f(i) = ka*(u(i)-uj)+kb*uj+sign(v(i))*f0;
else
    f(i) = kb*u(i)+sign(v(i))*f0;
end
end

%% PLOT
figure
plot(u,f,'k','linewidth',4)
set(gca,'FontSize',28)
set(gca,'FontName','Times New Roman')
xlabel('generalized displacement'), ylabel('generalized force')
grid
zoom off

Model formulation

In the algebraic model developed by Vaiana et al. (2019),[5] the generalized force at time $t$ , representing the output variable, is evaluated as a function of the generalized displacement as follows:

 $f_{t}=\beta _{1}u_{t}^{3}+\beta _{2}u_{t}^{5}+k_{b}u_{t}+\left(k_{a}-k_{b}\right)\left[{\frac {(1+s_{t}u_{t}-s_{t}u_{j}+2u_{0})^{1-\alpha }}{s_{t}(1-\alpha )}}-{\frac {(1+2u_{0})^{1-\alpha }}{s_{t}(1-\alpha )}}\right]+s_{t}f_{0}{\text{ when }}u_{t}s_{t}<u_{j}s_{t},$

 $f_{t}=\beta _{1}u_{t}^{3}+\beta _{2}u_{t}^{5}+k_{b}u_{t}+s_{t}f_{0}{\text{ when }}u_{t}s_{t}>u_{j}s_{t},$

where $k_{a},k_{b},\alpha$ , $\beta _{1}$ and $\beta _{2}$ are the five model parameters to be calibrated from experimental or numerical tests, whereas $s_{t}$ is the sign of the generalized velocity at time $t$ , that is, $s_{t}=\operatorname {sign} ({\dot {u}}_{t})$ . Furthermore, $u_{0}$ and $f_{0}$ are two internal model parameters evaluated as:

 $u_{0}={\frac {1}{2}}\left[\left({\frac {k_{a}-k_{b}}{10^{-20}}}\right)^{1/\alpha }-1\right],$

 $f_{0}={\frac {k_{a}-k_{b}}{2}}\left[{\frac {\left(1+2u_{0}\right)^{1-\alpha }-1}{1-\alpha }}\right],$

whereas $u_{j}$ is the history variable:

 $u_{j}=u_{t-\Delta t}+s_{t}(1+2u_{0})-s_{t}\left\lbrace {\frac {s_{t}(1-\alpha )}{k_{a}-k_{b}}}\left[f_{t-\Delta t}-\beta _{1}u_{t-\Delta t}^{3}-\beta _{2}u_{t-\Delta t}^{5}-k_{b}u_{t-\Delta t}-s_{t}f_{0}+(k_{a}-k_{b}){\frac {(1+2u_{0})^{1-\alpha }}{s_{t}(1-\alpha )}}\right]\right\rbrace ^{1/(1-\alpha )}.$

Hysteresis loop shapes

Figure 1.2 shows four different hysteresis loop shapes obtained by applying a sinusoidal generalized displacement having unit amplitude and frequency and simulated by adopting the Algebraic Model (AM) parameters listed in Table 1.2.

Figure 1.2. Hysteresis Loops reproduced by using the AM model parameters in Table 1.2

Table 1.2 - AM parameters
	$k_{a}$	$k_{b}$	$\alpha$	$\beta _{1}$	$\beta _{2}$
(a)	10.0	1.0	10.0	0.0	0.0
(b)	10.0	1.0	10.0	0.2	0.2
(c)	10.0	1.0	10.0	−0.2	−0.2
(d)	10.0	1.0	10.0	−1.2	1.2

Matlab code

%  =========================================================================================
%  September 2019
%  Algebraic Model Algorithm
%  Nicolò Vaiana, Post-Doctoral Researcher, PhD 
%  Department of Structures for Engineering and Architecture 
%  University of Naples Federico II
%  via Claudio, 21 - 80125, Napoli
%  =========================================================================================

clc; clear all; close all;

%% APPLIED DISPLACEMENT TIME HISTORY

dt = 0.001;                                                                %time step
t  = 0:dt:1.50;                                                            %time interval
a0 = 1;                                                                    %applied displacement amplitude
fr = 1;                                                                    %applied displacement frequency
u  = a0*sin((2*pi*fr)*t(1:length(t)));                                     %applied displacement vector
v  = 2*pi*fr*a0*cos((2*pi*fr)*t(1:length(t)));                             %applied velocity vector
n  = length(u);                                                            %applied displacement vector length

%% 1. INITIAL SETTINGS
%1.1 Set the five model parameters
ka    = 10.0;                                                              %model parameter
kb    = 1.0;                                                               %model parameter
alfa  = 10.0;                                                              %model parameter
beta1 = 0.0;                                                               %model parameter
beta2 = 0.0;                                                               %model parameter
%1.2 Compute the internal model parameters 
u0    = (1/2)*((((ka-kb)/10^-20)^(1/alfa))-1);                             %internal model parameter
f0    = ((ka-kb)/2)*((((1+2*u0)^(1-alfa))-1)/(1-alfa));                    %internal model parameter
%1.3 Initialize the generalized force vector
f     = zeros(1, n);

%% 2. CALCULATIONS AT EACH TIME STEP

for i = 2:n
%2.1 Update the history variable
uj = u(i-1)+sign(v(i))*(1+2*u0)-sign(v(i))*((((sign(v(i))*(1-alfa))/(ka-kb))*(f(i-1)-beta1*u(i-1)^3-beta2*u(i-1)^5-kb*u(i-1)-sign(v(i))*f0+(ka-kb)*(((1+2*u0)^(1-alfa))/(sign(v(i))*(1-alfa)))))^(1/(1-alfa)));
%2.2 Evaluate the generalized force at time t
if (sign(v(i))*uj)-2*u0 < sign(v(i))*u(i) || sign(v(i))*u(i) < sign(v(i))*uj
    f(i) = beta1*u(i)^3+beta2*u(i)^5+kb*u(i)+(ka-kb)*((((1+2*u0+sign(v(i))*(u(i)-uj))^(1-alfa))/(sign(v(i))*(1-alfa)))-(((1+2*u0)^(1-alfa))/(sign(v(i))*(1-alfa))))+sign(v(i))*f0;
else
    f(i) = beta1*u(i)^3+beta2*u(i)^5+kb*u(i)+sign(v(i))*f0;
end
end

%% PLOT
figure
plot(u, f, 'k', 'linewidth', 4)
set(gca, 'FontSize', 28)
set(gca, 'FontName', 'Times New Roman')
xlabel('generalized displacement'), ylabel('generalized force')
grid
zoom off

Transcendental models

In transcendental models, the output variable is computed by solving transcendental equations, namely equations involving trigonometric, inverse trigonometric, exponential, logarithmic, and/or hyperbolic functions.

Model formulation

In the exponential model developed by Vaiana et al. (2018),[4] the generalized force at time $t$ , representing the output variable, is evaluated as a function of the generalized displacement as follows:

 $f_{t}=-2\beta u_{t}+e^{\beta u_{t}}-e^{-\beta u_{t}}+k_{b}u_{t}-s_{t}{\frac {k_{a}-k_{b}}{\alpha }}\left[e^{-\alpha (u_{t}s_{t}-u_{j}s_{t}+2u_{0})}-e^{-2\alpha u_{0}}\right]+f_{0}s_{t}{\text{ when }}u_{t}s_{t}<u_{j}s_{t},$

 $f_{t}=-2\beta u_{t}+e^{\beta u_{t}}-e^{-\beta u_{t}}+k_{b}u_{t}+f_{0}s_{t}{\text{ when }}u_{t}s_{t}>u_{j}s_{t},$

where $k_{a},k_{b},\alpha$ and $\beta$ are the four model parameters to be calibrated from experimental or numerical tests, whereas $s_{t}$ is the sign of the generalized velocity at time $t$ , that is, $s_{t}=\operatorname {sign} ({\dot {u}}_{t})$ . Furthermore, $u_{0}$ and $f_{0}$ are two internal model parameters evaluated as:

 $u_{0}=-{\frac {1}{2\alpha }}\ln \left({\frac {10^{-20}}{k_{a}-k_{b}}}\right),$

 $f_{0}={\frac {k_{a}-k_{b}}{2\alpha }}\left(1-e^{-2\alpha u_{0}}\right),$

whereas $u_{j}$ is the history variable:

 $u_{j}=u_{t-\Delta t}+2u_{0}s_{t}+{\frac {s_{t}}{\alpha }}\ln \left[{\frac {\alpha s_{t}}{k_{a}-k_{b}}}\left(-2\beta u_{t-\Delta t}+e^{\beta u_{t-\Delta t}}-e^{-\beta u_{t-\Delta t}}+k_{b}u_{t-\Delta t}+{\frac {k_{a}-k_{b}}{\alpha }}s_{t}e^{-2\alpha u_{0}}+f_{0}s_{t}-f_{t-\Delta t}\right)\right].$

Hysteresis loop shapes

Figure 2.1 shows four different hysteresis loop shapes obtained by applying a sinusoidal generalized displacement having unit amplitude and frequency and simulated by adopting the Exponential Model (EM) parameters listed in Table 2.1.

Figure 2.1. Hysteresis Loops reproduced by using the EM model parameters in Table 2.1.

Table 2.1 - EM parameters
	$k_{a}$	$k_{b}$	$\alpha$	$\beta$
(a)	5.0	0.5	5.0	0.0
(b)	5.0	−0.5	5.0	0.0
(c)	5.0	0.5	5.0	1.0
(d)	5.0	0.5	5.0	−1.0

Matlab code

%  =========================================================================================
%  September 2019
%  Exponential Model Algorithm
%  Nicolò Vaiana, Post-Doctoral Researcher, PhD 
%  Department of Structures for Engineering and Architecture 
%  University of Naples Federico II
%  via Claudio, 21 - 80125, Napoli
%  =========================================================================================

clc; clear all; close all;

%% APPLIED DISPLACEMENT TIME HISTORY

dt = 0.001;                                                                %time step
t  = 0:dt:1.50;                                                            %time interval
a0 = 1;                                                                    %applied displacement amplitude
fr = 1;                                                                    %applied displacement frequency
u  = a0*sin((2*pi*fr)*t(1:length(t)));                                     %applied displacement vector
v  = 2*pi*fr*a0*cos((2*pi*fr)*t(1:length(t)));                             %applied velocity vector
n  = length(u);                                                            %applied displacement vector length

%% 1. INITIAL SETTINGS
%1.1 Set the four model parameters
ka    = 5.0;                                                               %model parameter
kb    = 0.5;                                                               %model parameter
alfa  = 5.0;                                                               %model parameter
beta  = 1.0;                                                               %model parameter
%1.2 Compute the internal model parameters 
u0    = -(1/(2*alfa))*log(10^-20/(ka-kb));                                 %internal model parameter
f0    = ((ka-kb)/(2*alfa))*(1-exp(-2*alfa*u0));                            %internal model parameter
%1.3 Initialize the generalized force vector
f     = zeros(1, n);

%% 2. CALCULATIONS AT EACH TIME STEP

for i = 2:n
%2.1 Update the history variable
uj = u(i-1)+2*u0*sign(v(i))+sign(v(i))*(1/alfa)*log(sign(v(i))*(alfa/(ka-kb))*(-2*beta*u(i-1)+exp(beta*u(i-1))-exp(-beta*u(i-1))+kb*u(i-1)+sign(v(i))*((ka-kb)/alfa)*exp(-2*alfa*u0)+sign(v(i))*f0-f(i-1)));
%2.2 Evaluate the generalized force at time t
if (sign(v(i))*uj)-2*u0 < sign(v(i))*u(i) || sign(v(i))*u(i) < sign(v(i))*uj
    f(i) = -2*beta*u(i)+exp(beta*u(i))-exp(-beta*u(i))+kb*u(i)-sign(v(i))*((ka-kb)/alfa)*(exp(-alfa*(sign(v(i))*(u(i)-uj)+2*u0))-exp(-2*alfa*u0))+sign(v(i))*f0;
else
    f(i) = -2*beta*u(i)+exp(beta*u(i))-exp(-beta*u(i))+kb*u(i)+sign(v(i))*f0;
end
end

%% PLOT
figure
plot(u ,f, 'k', 'linewidth', 4)
set(gca, 'FontSize', 28)
set(gca, 'FontName', 'Times New Roman')
xlabel('generalized displacement'), ylabel('generalized force')
grid
zoom off

References

Vaiana, Nicolò; Spizzuoco, Mariacristina; Serino, Giorgio (June 2017). "Wire rope isolators for seismically base-isolated lightweight structures: Experimental characterization and mathematical modeling". Engineering Structures. 140: 498–514. doi:10.1016/j.engstruct.2017.02.057.
Dimian, Mihai; Andrei, Petru (4 November 2013). Noise-driven phenomena in hysteretic systems. ISBN 9781461413745.
Vaiana, Nicolò; Sessa, Salvatore; Rosati, Luciano (January 2021). "A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena". Mechanical Systems and Signal Processing. 146: 106984. doi:10.1016/j.ymssp.2020.106984.
Vaiana, Nicolò; Sessa, Salvatore; Marmo, Francesco; Rosati, Luciano (26 April 2018). "A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials". Nonlinear Dynamics. 93 (3): 1647–1669. doi:10.1007/s11071-018-4282-2.
Vaiana, Nicolò; Sessa, Salvatore; Marmo, Francesco; Rosati, Luciano (March 2019). "An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings". Composite Structures. 211: 196–212. doi:10.1016/j.compstruct.2018.12.017.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Vaiana, Nicolò; Spizzuoco, Mariacristina; Serino, Giorgio (June 2017). "Wire rope isolators for seismically base-isolated lightweight structures: Experimental characterization and mathematical modeling". Engineering Structures. 140: 498–514. doi:10.1016/j.engstruct.2017.02.057.

[2] Dimian, Mihai; Andrei, Petru (4 November 2013). Noise-driven phenomena in hysteretic systems. ISBN 9781461413745.

[3] Vaiana, Nicolò; Sessa, Salvatore; Rosati, Luciano (January 2021). "A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena". Mechanical Systems and Signal Processing. 146: 106984. doi:10.1016/j.ymssp.2020.106984.

[:0-4] Vaiana, Nicolò; Sessa, Salvatore; Marmo, Francesco; Rosati, Luciano (26 April 2018). "A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials". Nonlinear Dynamics. 93 (3): 1647–1669. doi:10.1007/s11071-018-4282-2.

[5] Vaiana, Nicolò; Sessa, Salvatore; Marmo, Francesco; Rosati, Luciano (March 2019). "An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings". Composite Structures. 211: 196–212. doi:10.1016/j.compstruct.2018.12.017.