Image formation
The study of image formation encompasses the radiometric and geometric processes by which 2D images of 3D objects are formed. In the case of digital images, the image formation process also includes analog to digital conversion and sampling.
Imaging
The imaging process is a mapping of an object to an image plane. Each point on the image corresponds to a point on the object. An illuminated object will scatter light toward a lens and the lens will collect and focus the light to create the image. The ratio of the height of the image to the height of the object is the magnification. The spatial extent of the image surface and the focal length of the lens determine the field of view of the lens.
Illumination
An object may be illuminated by the light from an emitting source such as the sun, a light bulb or a Light Emitting Diode. The light incident on the object is reflected in a manner dependent on the surface properties of the object. For rough surfaces, the reflected light is scattered in a manner described by the Bi-directional Reflectance Distribution Function (BRDF) of the surface. The BRDF of a surface is the ratio of the exiting power per square meter per steradian (radiance) to the incident power per square meter (irradiance).[1] The BRDF typically varies with angle and may vary with wavelength, but a specific important case is a surface that has constant BRDF. This surface type is referred to as Lambertian and the magnitude of the BRDF is R/π, where R is the reflectivity of the surface. The portion of scattered light that propagates toward the lens is collected by the entrance pupil of the imaging lens over the field of view.
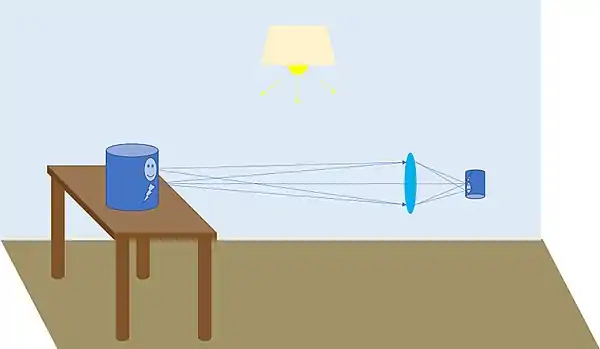
Field of view and imagery
The Field of view of a lens is limited by the size of the image plane and the focal length of the lens. The relationship between a location on the image and a location on the object is y = f*tan(θ), where y is the max extent of the image plane, f is the focal length of the lens and θ is the field of view. If y is the max radial size of the image then θ is the field of view of the lens. While the image created by a lens is continuous, it can be modeled as a set of discrete field points, each representing a point on the object. The quality of the image is limited by the aberrations in the lens and the diffraction created by the finite aperture stop.
Pupils and stops
The aperture stop of a lens is a mechanical aperture which limits the light collection for each field point. The entrance pupil is the image of the aperture stop created by the optical elements on the object side of the lens. The light scattered by an object is collected by the entrance pupil and focused onto the image plane via a series of refractive elements. The cone of the focused light at the image plane is set by the size of the entrance pupil and the focal length of the lens. This is often referred to as the f-stop or f-number of the lens. f/# = f/D where D is the diameter of the entrance pupil.
Pixelation and color vs. monochrome
In typical digital imaging systems, a sensor is placed at the image plane. The light is focused on to the sensor and the continuous image is pixelated. The light incident on each pixel in the sensor will be integrated within the pixel and a proportional electronic signal will be generated.[2] The angular geometric resolution of a pixel is given by atan(p/f), where p is the pitch of the pixel. This is also called the pixel field of view. The sensor may be monochrome or color. In the case of a monochrome sensor, the light incident on each pixel is integrated and the resulting image is a grayscale like picture. For color images, a mosaic color filter is typically placed over the pixels to create a color image. An example is a Bayer filter. The signal incident on each pixel is then digitized to a bit stream.
Image quality
The quality of an image is dependent upon both geometric and physical items. Geometrically, higher density of pixels across an image will give less blocky pixelation and thus a better geometric image quality. Lens aberrations also contribute to the quality of the image. Physically, diffraction due to the aperture stop will limit the resolvable spatial frequencies as a function of f-number.
In the frequency domain, Modulation Transfer Function (MTF) is a measure of the quality of the imaging system. The MTF is a measure of the visibility of a sinusoidal variation in irradiance on the image plane as a function of the frequency of the sinusoid. It includes the effects of diffraction, aberrations and pixelation. For the lens, the MTF is the autocorrelation of the pupil function,[3] so it accounts for the finite pupil extent and the lens aberrations. The sensor MTF is the Fourier Transform of the pixel geometry. For a square pixel, MTF(ξ) = sin(πξp)/πξp where p is the pixel width and ξ is the spatial frequency. The MTF of the combination of the lens and detector is the product of the two component MTFs.
Perception
Color images can be perceived via two means. In the case of computer vision the light incident on the sensor comprises the image. In the case of visual perception, the human eye has a color dependent response to light so this must be accounted for. This is important consideration when converting to grayscale.
Image formation in eye
The principal difference between the lens of the eye and an ordinary optical lens is that the former is flexible. The radius of the curvature of the anterior surface of the lens is greater than the radius of its posterior surface. The shape of the lens is controlled by tension in the fibers of the ciliary body. To focus on distant objects, the controlling muscles cause the lens to be relatively flattened. Similarly, these muscles allow the lens to become thicker in order to focus on objects near the eye.
The distance between the center of the lens and the retina (focal length) varies from approximately 17 mm to about 14 mm, as the refractive power of the lens increases from its minimum to its maximum. When the eye focuses on an object farther away than about 3 m, the lens exhibits its lowest refractive power. When the eye focuses on a close object, the lens is most strongly refractive.
References
- Ross., McCluney (1994). Introduction to radiometry and photometry. Boston: Artech House. ISBN 0890066787. OCLC 30031974.
- E., Umbaugh, Scott (2017). Digital Image Processing and Analysis with MATLAB and CVIPtools, Third Edition (3rd ed.). ISBN 9781498766029. OCLC 1016899766.
- W., Goodman, Joseph (1996). Introduction to Fourier optics (2nd ed.). New York: McGraw-Hill. ISBN 0070242542. OCLC 35242460.