Incremental deformations

Scheme of the incremental deformation

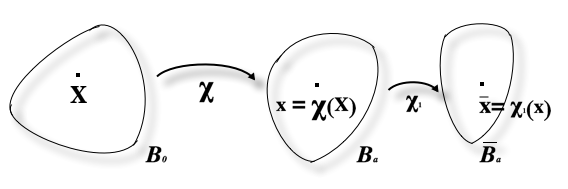
Let ${\displaystyle {\mathcal {E}}\in \mathbb {R} ^{3}}$ be a three-dimensional Euclidean space. Let ${\displaystyle {\mathcal {B}}_{0},{\mathcal {B}}_{a}\in {\mathcal {E}}}$ be two regions occupied by the material in two different instants of time. Let ${\displaystyle {\bf {\chi }}}$ be the deformation which transforms the tissue from ${\displaystyle {\mathcal {B}}_{0}}$, i.e. the material/reference configuration, to the loaded configuration ${\displaystyle {\mathcal {B}}_{a}}$, i.e. current configuration. Let ${\displaystyle \chi }$ be a ${\displaystyle C^{1}}$-diffeomorphism[7] from ${\displaystyle {\mathcal {B}}_{0}}$ to ${\displaystyle {\mathcal {B}}_{a}}$, with ${\displaystyle {\bf {x}}={\bf {\chi }}({\bf {X}})}$ being the current position vector, given as a function of the material position ${\displaystyle {\bf {X}}}$. The deformation gradient[5] is given by

Considering a hyperelastic material with an elastic strain energy density[5] ${\displaystyle W({\bf {F}})}$, the Piola-Kirchhoff stress tensor ${\displaystyle {\bf {S}}}$ is given by ${\displaystyle {\bf {S}}={\frac {\partial W}{\partial \,{\bf {F}}}}}$.

For a quasi-static problem, without body forces, the equilibrium equation is

${\displaystyle {\begin{aligned}{\rm {Div}}\,{\bf {S}}&=0&&\qquad {\text{Equilibrium}},\\[3pt]\end{aligned}}}$

where ${\displaystyle {\rm {Div}}}$ is the divergence[1] with respect to the material coordinates.

If the material is incompressible,[8] i.e. the volume of every subdomains does not change during the deformation, a Lagrangian multiplier[9] is typically introduced to enforce the internal isochoric constraint ${\displaystyle {\rm {det}}\,{\bf {F}}=1}$. So that, the expression of the Piola stress tensor becomes

${\displaystyle {\begin{aligned}{\bf {S}}&={\frac {\partial W}{\partial {\bf {F}}}}-p{\bf {F}}^{-1}&&\qquad {\text{Definition of the stress}}.\\\end{aligned}}}$

Let ${\displaystyle \partial {\mathcal {B}}_{0}}$ be the boundary of ${\displaystyle {\mathcal {B}}_{0}}$, the reference configuration, and ${\displaystyle \partial {\mathcal {B}}_{a}}$, the boundary of ${\displaystyle {\mathcal {B}}_{a}}$, the current configuration.[1] One defines the subset ${\displaystyle \Gamma _{D}}$ of ${\displaystyle \partial {\mathcal {B}}_{0}}$ on which Dirichlet conditions are applied, while Neumann conditions hold on ${\displaystyle \Gamma _{N}}$, such that ${\displaystyle \partial {\mathcal {B}}_{0}=\Gamma _{D}\cup \Gamma _{N}}$. If ${\displaystyle {\bf {u}}_{0}^{*}}$ is the displacement vector to be assigned at the portion ${\displaystyle \Gamma _{D}}$ and ${\displaystyle {\bf {t}}_{0}^{*}}$ is the traction vector to be assigned to the portion ${\displaystyle \Gamma _{N}}$, the boundary conditions can be written in mixed-form, such as

${\displaystyle {\begin{aligned}{\bf {u}}({\bf {{X})}}&={\bf {u}}_{0}^{*}&&\qquad {\rm {on}}\,\Gamma _{D},\\[3pt]{\bf {S}}^{\rm {T}}\cdot {\bf {N}}&={\bf {t}}_{0}^{*}&&\qquad {\rm {on}}\,\Gamma _{N},\\[3pt]\end{aligned}}}$

where ${\displaystyle {\bf {u}}={\bf {x}}-{\bf {X}}=\chi ({\bf {X}})-{\bf {X}}}$ is the displacement and the vector ${\displaystyle {\bf {N}}}$ is the unit outward normal to ${\displaystyle \partial {\mathcal {B}}_{0}}$.

The defined problem is called the boundary value problem (BVP). Hence, let ${\displaystyle {\bf {x}}^{0}=\chi ^{0}({\bf {X}})}$ be a solution of the BVP. Since ${\displaystyle W}$ depends nonlinearly[10] on the deformation gradient, this solution is generally not unique, and it depends on geometrical and material parameters of the problem. So, one has to employ the method of incremental deformation in order to highlight the existence of an adjacent solution for a critical value of a dimensionless parameter, called control parameter ${\displaystyle \gamma }$ which "controls" the onset of the instability.[11] This means that by increasing the value of this parameter, at a certain point new solutions appear. Hence, the selected basic solution is not anymore the stable one but it becomes unstable. In a physical way, at a certain time the stored energy, such as the integral of the density ${\displaystyle W}$ over all the domain of the basic solution is bigger than the one of the new solutions. To restore the equilibrium, the configuration of the material moves to another configuration which has lower energy.[12]

The perturbed deformation gradient is given by:

${\displaystyle {\bar {\bf {F}}}={\bf {F}}^{0}+\delta {\bf {F}}=(\mathbf {I} +\mathbf {\Gamma } ){\bf {F}}^{0}}$,

where ${\displaystyle \mathbf {\Gamma } ={\rm {grad}}\,\chi ^{1}({\bf {x}}^{0})}$, where ${\displaystyle {\rm {grad}}}$ is the gradient operator with respect to the current configuration.

The perturbed Piola stress is given by:

${\displaystyle {\bar {\bf {S}}}={\bf {S}}^{0}+\delta {\bf {S}}={\bf {S}}^{0}+{\frac {\partial {\bf {S}}^{0}}{\partial {\bf {F}}}}{\bigg |}_{{\bf {F}}^{0}}:\delta {\bf {F}}}$

where ${\displaystyle$ :} denotes the contraction between two tensors, a forth-order tensor ${\displaystyle {\frac {\partial {\bf {S}}^{0}}{\partial {\bf {F}}}}{\bigg |}_{{\bf {F}}^{0}}={\mathcal {A}}^{1}}$ and a second-order tensor ${\displaystyle \delta {\bf {F}}}$. Since ${\displaystyle {\bf {S}}}$ depends on ${\displaystyle {\bf {F}}}$ through ${\displaystyle W}$, its expression can be rewritten by emphasizing this dependence, such as

${\displaystyle {\bar {\bf {S}}}={\frac {\partial W}{\partial {\bf {F}}}}{\bigg |}_{{\bf {F}}^{0}}+{\frac {\partial W}{\partial {\bf {F}}\partial {\bf {F}}}}{\bigg |}_{{\bf {F}}^{0}}:\delta {\bf {F}}.}$

If the material is incompressible, one gets

${\displaystyle \delta {\bf {S}}={\frac {\partial {\bf {S}}^{0}}{\partial {\bf {F}}}}\delta {\bf {F}}={\mathcal {A}}^{1}\delta {\bf {F}}+p({\bf {F}}^{0})^{-1}\delta {\bf {F}}({\bf {F}}^{0})^{-1}-\delta p\,({\bf {F}}^{0})^{-1},}$

where ${\displaystyle \delta p}$ is the increment in ${\displaystyle p}$ and ${\displaystyle {\mathcal {A}}^{1}}$ is called the elastic moduli associated to the pairs ${\displaystyle ({\bf {S}},{\bf {F}})}$.

It is useful to derive the push-forward of the perturbed Piola stress be defined as

${\displaystyle \delta {\bf {S}}_{0}={\bf {F}}^{0}\,\delta {\bf {S}}={\mathcal {A}}_{0}^{1}\Gamma +p\Gamma -\delta p\,{\rm {I}},}$

where ${\displaystyle {\mathcal {A}}_{0}^{1}}$ is also known as the tensor of instantaneous moduli, whose components are:

${\displaystyle ({\mathcal {A}}_{0}^{1})_{ijhk}={\bf {F}}_{i\gamma }^{0}\,{\bf {F}}_{h\beta }^{0}\,{\mathcal {A}}_{\gamma j\beta k}^{1}}$.

Expanding the equilibrium equation around the basic solution, one gets

${\displaystyle {\rm {Div}}({\bar {\bf {S}}})={\rm {Div}}({\bf {S}}^{0}+\delta {\bf {S}})={\rm {Div}}({\bf {S}}^{0})+\,{\rm {Div}}(\delta {\bf {S}})=0.}$

Since ${\displaystyle {\bf {S}}^{0}}$ is the solution to the equation at the zero-order, the incremental equation can be rewritten as

${\displaystyle {\rm {div}}(\delta {\bf {S}}_{0})=0,}$

where ${\displaystyle {\rm {div}}}$ is the divergence operator with respect to the actual configuration.

The incremental incompressibility constraint reads

${\displaystyle {\begin{aligned}{\rm {det}}\,({\bf {F}}^{0}+\delta {\bf {F}})&=1.\\\end{aligned}}}$

Expanding this equation around the basic solution, as before, one gets

${\displaystyle {\rm {tr}}(\mathbf {\Gamma } )=0.}$

Let ${\displaystyle {\overline {\delta {\bf {u}}}}}$ and ${\displaystyle {\overline {\delta {\bf {t}}}}}$ be the prescribed increment of ${\displaystyle {\bf {u}}_{0}^{*}}$ and ${\displaystyle {\bf {t}}_{0}^{*}}$ respectively. Hence, the perturbed boundary condition are

${\displaystyle {\begin{aligned}\delta {\bf {u}}({\bf {x}})&={\overline {\delta {\bf {u}}}}&&\qquad {\bf {x}}\in {\Gamma _{D}}\\[3pt]\delta {\bf {S}}_{0}^{\rm {T}}\cdot {\bf {n}}&={\overline {\delta {\bf {t}}}}&&\qquad {\bf {x}}\in {\Gamma _{N}},\\[3pt]\end{aligned}}}$

where ${\displaystyle \delta {\bf {u}}=\chi ^{1}({\bf {x}}^{0})-{\bf {x}}}$ is the incremental displacement and ${\displaystyle {\Gamma _{D}}\cup {\Gamma _{N}}={\partial \Omega }}$.

Result of the linear stability analysis.

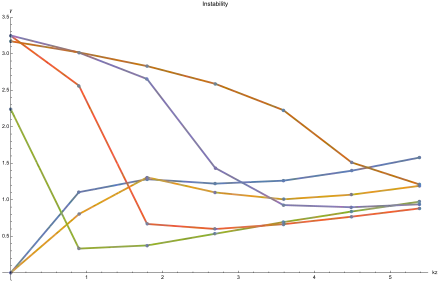
The Stroh formalism provides an optimal form to solve a great variety of elastic problems. Optimal means that one can construct an efficient numerical procedure to solve the incremental problem. By solving the incremental boundary value problem, one finds the relations[18] among the material and geometrical parameters of the problem and the perturbation modes by which the wave propagates in the material, i.e. what denotes the instability. Everything depends on ${\displaystyle \gamma }$, the selected parameter denoted as the control one.

By this analysis, in a graph perturbation mode vs control parameter, the minimum value of the perturbation mode represents the first mode at which one can see the onset of the instability. For instance, in the picture, the first value of the mode ${\displaystyle kz}$ in which the instability emerges is around ${\displaystyle 0.3}$ since the trivial solution ${\displaystyle \gamma =0}$ and ${\displaystyle kz=0}$ does not have to be considered.