Lamé's special quartic

Lamé's special quartic, named after Gabriel Lamé, is the graph of the equation

x^{4}+y^{4}=r^{4}

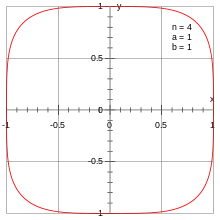
Lamé's special quartic with "radius" 1.

where $r>0$ .[1] It looks like a rounded square with "sides" of length $2r$ and centered on the origin. This curve is a squircle centered on the origin, and it is a special case of a superellipse.[2]

Because of Pierre de Fermat's only surviving proof, that of the n = 4 case of Fermat's Last Theorem, if r is rational there is no non-trivial rational point (x, y) on this curve (that is, no point for which both x and y are non-zero rational numbers).

References

Oakley, Cletus Odia (1958), Analytic Geometry Problems, College Outline Series, 108, Barnes & Noble, p. 171.
Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 212, ISBN 9780883855119.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Oakley, Cletus Odia (1958), Analytic Geometry Problems, College Outline Series, 108, Barnes & Noble, p. 171.

[2] Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 212, ISBN 9780883855119.