Lamination (topology)
In topology, a branch of mathematics, a lamination is a :
- "topological space partitioned into subsets"[1]
- decoration (a structure or property at a point) of a manifold in which some subset of the manifold is partitioned into sheets of some lower dimension, and the sheets are locally parallel.

Lamination associated with Mandelbrot set

Lamination of rabbit Julia set
A lamination of a surface is a partition of a closed subset of the surface into smooth curves.
It may or may not be possible to fill the gaps in a lamination to make a foliation.[2]
Examples
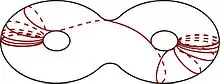
Geodesic lamination of a closed surface
- A geodesic lamination of a 2-dimensional hyperbolic manifold is a closed subset together with a foliation of this closed subset by geodesics.[3] These are used in Thurston's classification of elements of the mapping class group and in his theory of earthquake maps.
- Quadratic laminations, which remain invariant under the angle doubling map.[4] These laminations are associated with quadratic maps.[5][6] It is a closed collection of chords in the unit disc.[7] It is also topological model of Mandelbrot or Julia set.
See also
Notes
- "Lamination", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Defs.txt". Archived from the original on 2009-07-13. Retrieved 2009-07-13. Oak Ridge National Laboratory
- Laminations and foliations in dynamics, geometry and topology: proceedings of the conference on laminations and foliations in dynamics, geometry and topology, May 18-24, 1998, SUNY at Stony Brook
- Houghton, Jeffrey. "Useful Tools in the Study of Laminations" Paper presented at the annual meeting of the Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA, Aug 05, 2010
- Tomoki KAWAHIRA: Topology of Lyubich-Minsky's laminations for quadratic maps: deformation and rigidity (3 heures)
- Topological models for some quadratic rational maps by Vladlen Timorin
- Modeling Julia Sets with Laminations: An Alternative Definition by Debra Mimbs Archived 2011-07-07 at the Wayback Machine
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.