Moving sofa problem
In mathematics, the moving sofa problem or sofa problem is a two-dimensional idealisation of real-life furniture-moving problems and asks for the rigid two-dimensional shape of largest area A that can be maneuvered through an L-shaped planar region with legs of unit width.[1] The area A thus obtained is referred to as the sofa constant. The exact value of the sofa constant is an open problem.
| Unsolved problem in mathematics: What is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor? (more unsolved problems in mathematics) |
History
The first formal publication was by the Austrian-Canadian mathematician Leo Moser in 1966, although there had been many informal mentions before that date.[1]
Lower and upper bounds
Work has been done on proving that the sofa constant cannot be below or above certain values (lower bounds and upper bounds).
Lower bounds
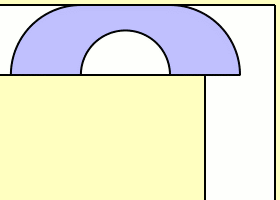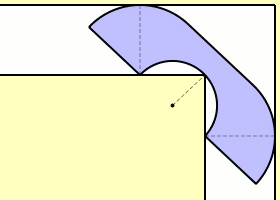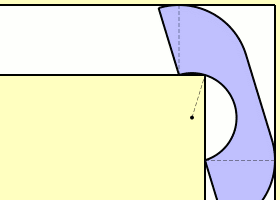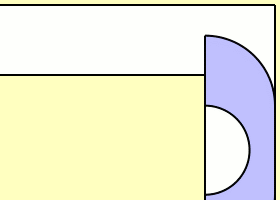

An obvious lower bound is . This comes from a sofa that is a half-disk of unit radius, which can rotate in the corner.
John Hammersley derived a lower bound of based on a shape resembling a telephone handset, consisting of two quarter-disks of radius 1 on either side of a 1 by 4/π rectangle from which a half-disk of radius has been removed.[2][3]
Joseph Gerver found a sofa described by 18 curve sections each taking a smooth analytic form. This further increased the lower bound for the sofa constant to approximately 2.2195.[4][5]
A computation by Philip Gibbs produced a shape indistinguishable from that of Gerver's sofa giving a value for the area equal to eight significant figures.[6] This is evidence that Gerver's sofa is indeed the best possible but it remains unproven.
Ambidextrous sofa

A variant of the sofa problem asks the shape of largest area that can go round both left and right 90 degree corners in a corridor of unit width. A lower bound of area approximately 1.64495521 has been described by Dan Romik. His sofa is also described by 18 curve sections.[9][10]
See also
- Dirk Gently's Holistic Detective Agency – novel by Douglas Adams, a subplot of which revolves around such a problem.
- Mountain climbing problem
- Moser's worm problem
- "The One with the Cop" - an episode of the American TV series Friends a subplot revolving around such a problem.
References
- Wagner, Neal R. (1976). "The Sofa Problem" (PDF). The American Mathematical Monthly. 83 (3): 188–189. doi:10.2307/2977022. JSTOR 2977022.
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1994). Halmos, Paul R. (ed.). Unsolved Problems in Geometry. Problem Books in Mathematics; Unsolved Problems in Intuitive Mathematics. II. Springer-Verlag. ISBN 978-0-387-97506-1. Retrieved 24 April 2013.
- Moving Sofa Constant by Steven Finch at MathSoft, includes a diagram of Gerver's sofa.
- Gerver, Joseph L. (1992). "On Moving a Sofa Around a Corner". Geometriae Dedicata. 42 (3): 267–283. doi:10.1007/BF02414066. ISSN 0046-5755.
- Weisstein, Eric W. "Moving sofa problem". MathWorld.
- Gibbs, Philip, A Computational Study of Sofas and Cars
- Stewart, Ian (January 2004). Another Fine Math You've Got Me Into... Mineola, N.Y.: Dover Publications. ISBN 0486431819. Retrieved 24 April 2013.
- Kallus, Yoav; Romik, Dan (December 2018). "Improved upper bounds in the moving sofa problem". Advances in Mathematics. 340: 960–982. arXiv:1706.06630. doi:10.1016/j.aim.2018.10.022. ISSN 0001-8708.
- Romik, Dan (2017). "Differential equations and exact solutions in the moving sofa problem". Experimental Mathematics. 26 (2): 316–330. arXiv:1606.08111. doi:10.1080/10586458.2016.1270858.
- Romik, Dan. "The moving sofa problem - Dan Romik's home page". UCDavis. Retrieved 26 March 2017.
External links
- Romik, Dan (March 23, 2017). "The Moving Sofa Problem" (video). YouTube. Brady Haran. Retrieved 24 March 2017.
- SofaBounds - Program to calculate bounds on the sofa moving problem.
- A 3D model of Romik's ambidextrous sofa