Shifting balance theory

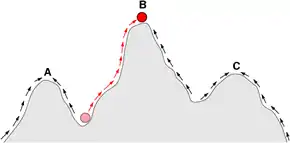
The shifting balance theory is a theory of evolution proposed in 1932 by Sewall Wright, suggesting that adaptive evolution may proceed most quickly when a population divides into subpopulations with restricted gene flow. The name of the theory is borrowed from Wright's metaphor of fitness landscapes (evolutionary landscapes), attempting to explain how a population may move across an adaptive valley to a higher adaptive peak. According to the theory, this movement occurs in three steps:

1. Genetic drift allows a locally adapted subpopulation to move across an adaptive valley to the base of a higher adaptive peak.
2. Natural selection will move the subpopulation up the higher peak.
3. This new superiorly adapted subpopulation may then expand its range and outcompete or interbreed with other subpopulations, causing the spread of new adaptations and movement of the global population toward the new fitness peak.

Sketch of a fitness landscape. The arrows indicate the preferred flow of a population on the landscape. The red ball indicates a population that moves from an adaptive valley to the top of an adaptive peak. Under a strict regime of natural selection (which usually acts to increase fitness in a population), it is not possible for a population at peak A to reach peak B because this requires descending into an adaptive valley. Shifting balance theory aims to explain how this may be possible.

Although shifting balance theory has been influential in evolutionary biology, inspiring the theories of quantum evolution and punctuated equilibrium,[1] little empirical evidence exists to support the shifting balance process as an important factor in evolution.[2]