Square-free word
In combinatorics, a squarefree word is a word (a sequence of symbols) that does not contain any squares. A square is a word of the form XX, where X is not empty. Thus, a squarefree word can also be defined as a word that avoids the pattern XX.
Finite squarefree words
Binary alphabet
Over a binary alphabet , the only squarefree words are the empty word , and .
Ternary alphabet
Over a ternary alphabet , there are infinitely many squarefree words. It is possible to count the number of ternary squarefree words of length n.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 12 | 18 | 30 | 42 | 60 | 78 | 108 | 144 | 204 | 264 |
This number is bounded by , where .[2] The upper bound on can be found via Fekete's Lemma and approximation by automata. The lower bound can be found by finding a substitution that preserves squarefreeness.[2]
Alphabet with more than three letters
Since there are infinitely many squarefree words over three-letter alphabets, this implies there are also infinitely many squarefree words over an alphabet with more than three letters.
The following table shows the exact growth rate of the k-ary squarefree words:
| alphabet size (k) | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| growth rate | 2.6215080 | 3.7325386 | 4.7914069 | 5.8284661 | 6.8541173 | 7.8729902 |
| alphabet size (k) | 10 | 11 | 12 | 13 | 14 | 15 |
| growth rate | 8.8874856 | 9.8989813 | 10.9083279 | 11.9160804 | 12.9226167 | 13.9282035 |
2-dimensional words
Consider a map from to A, where A is an alphabet and is called a 2-dimensional word. Let be the entry . A word is a line of if there exists such that , and for .[3]
Carpi[4] proves that there exists a 2-dimensional word over a 16-letter alphabet such that every line of is squarefree. A computer search shows that there are no 2-dimensional words over a 7-letter alphabet, such that every line of is squarefree.
Generating finite squarefree words
Shur[5] proposes an algorithm called R2F (random-t(w)o-free) that can generate a squarefree word of length n over any alphabet with three or more letters. This algorithm is based on a modification of entropy compression: it randomly selects letters from a k-letter alphabet to generate a -ary squarefree word.
algorithm R2F is
input: alphabet size ,
word length
output: a -ary squarefree word wof length n.
(Note that is the alphabet with letters .)
(For a word , is the permutation of such that a precedes b in if the
right most position of a in w is to the right of the rightmost position of b in w.
For example, has .)
choose in uniformly at random
set to followed by all other letters of in increasing order
set the number N of iterations to 0
while do
choose j in uniformly at random
append to the end of w
update shifting the first j elements to the right and setting
increment N by 1
if w ends with an square of rank r then
delete the last r letters of w
return w
Every (k+1)-ary squarefree word can be the output of Algorithm R2F, because on each iteration it can append any letter except for the last letter of w.
The expected number of random k-ary letters used by Algorithm R2F to construct a -ary squarefree word of length n is
Note that there exists an algorithm that can verify the squarefreeness of a word of length n in time. Apostolico and Preparata[6] give an algorithm using suffix trees. Crochemore[7] uses partitioning in his algorithm. Main and Lorentz[8] provide an algorithm based on the divide-and-conquer method. A naive implementation may require time to verify the squarefreeness of a word of length n.
Infinite squarefree words
There exist arbitrarily long squarefree words in any alphabet with three or more letters, as proved by Axel Thue.[9]
First difference of the Thue–Morse sequence
One example of an infinite squarefree word over an alphabet of size 3 is the word over the alphabet obtained by taking the first difference of the Thue–Morse sequence.[9] That is, from the Thue–Morse sequence
one forms a new sequence in which each term is the difference of two consecutive terms of the Thue–Morse sequence. The resulting squarefree word is
Leech's morphism
Another example found by John Leech[10] is defined recursively over the alphabet . Let be any squarefree word starting with the letter 0. Define the words recursively as follows: the word is obtained from by replacing each 0 in with 0121021201210, each 1 with 1202102012021, and each 2 with 2010210120102. It is possible to prove that the sequence converges to the infinite squarefree word
- 0121021201210120210201202120102101201021202102012021...
Generating infinite squarefree words
Infinite squarefree words can be generated by squarefree morphism. A morphism is called squarefree if the image of every squarefree word is squarefree. A morphism is called k–squarefree if the image of every squarefree word of length k is squarefree.
Crochemore[11] proves that a uniform morphism h is squarefree if and only if it is 3-squarefree. In other words, h is squarefree if and only if is squarefree for all squarefree w of length 3. It is possible to find a squarefree morphism by brute-force search.
algorithm squarefree_morphism is
output: a squarefree morphism with the lowest possible rank k.
set
while True do
set k_sf_words to the list of all squarefree words of length k over a ternary alphabet
for each in k_sf_words do
for each in k_sf_words do
for each in k_sf_words do
if then
break from the current loop (advance to next )
if and then
if is squarefree for all squarefree w of length 3 then
return
increment k by 1
Over a ternary alphabet, there are exactly 144 uniform squarefree morphisms of rank 11 and no uniform squarefree morphisms with a lower rank than 11.
To obtain an infinite squarefree words, start with any squarefree word such as 0, and successively apply a squarefree morphism h to it. The resulting words preserve the property of squarefreeness. For example, let h be a squarefree morphism, then as , is an infinite squarefree word.
Note that, if a morphism over a ternary alphabet is not uniform, then this morphism is squarefree if and only if it is 5-squarefree.[11]
Letter combinations in squarefree words
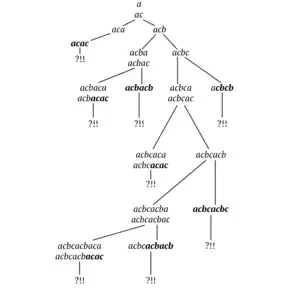
Avoid two-letter combinations
Over a ternary alphabet, a squarefree word of length more than 13 contains all the squarefree two-letter combinations.[12]
This can be proved by constructing a squarefree word without the two-letter combination ab. As a result, bcbacbcacbaca is the longest squarefree word without the combination ab and its length is equal to 13.
Note that over a more than three-letter alphabet there are squarefree words of any length without an arbitrary two-letter combination.
Avoid three-letter combinations
Over a ternary alphabet, a squarefree word of length more than 36 contains all the squarefree three-letter combinations.[12]
However, there are squarefree words of any length without the three-letter combination aba.
Note that over a more than three-letter alphabet there are squarefree words of any length without an arbitrary three-letter combination.
Density of a letter
The density of a letter a in a finite word w is defined as where is the number of occurrences of a in and is the length of the word. The density of a letter a in an infinite word is where is the prefix of the word w of length l.[13]
The minimal density of a letter a in an infinite ternary squarefree word is equal to .[13]
The maximum density of a letter a in an infinite ternary squarefree word is equal to .[14]
Notes
- "A006156 - OEIS". oeis.org. Retrieved 2019-03-28.
- Shur, Arseny (2011). "Growth properties of power-free languages". Computer Science Review. 6 (5–6): 28–43. doi:10.1016/j.cosrev.2012.09.001.
- Berthe, Valerie; Rigo, Michel, eds. (2016), "Preface", Combinatorics, Words and Symbolic Dynamics, Cambridge University Press, pp. xi–xviii, doi:10.1017/cbo9781139924733.001, ISBN 9781139924733
- Carpi, Arturo (1988). "Multidimensional unrepetitive configurations". Theoretical Computer Science. 56 (2): 233–241. doi:10.1016/0304-3975(88)90080-1. ISSN 0304-3975.
- Shur, Arseny (2015). "Generating square-free words efficiently". Theoretical Computer Science. 601: 67–72. doi:10.1016/j.tcs.2015.07.027.
- Apostolico, A.; Preparata, F.P. (Feb 1983). "Optimal off-line detection of repetitions in a string". Theoretical Computer Science. 22 (3): 297–315. doi:10.1016/0304-3975(83)90109-3. ISSN 0304-3975.
- Crochemore, Max (Oct 1981). "An optimal algorithm for computing the repetitions in a word". Information Processing Letters. 12 (5): 244–250. doi:10.1016/0020-0190(81)90024-7. ISSN 0020-0190.
- Main, Michael G; Lorentz, Richard J (Sep 1984). "An O(n log n) algorithm for finding all repetitions in a string". Journal of Algorithms. 5 (3): 422–432. doi:10.1016/0196-6774(84)90021-x. ISSN 0196-6774.
- Berstel, Jean (1994). Axel Thue's papers on repetitions in words a translation. Départements de mathématiques et d'informatique, Université du Québec à Montréal. ISBN 978-2892761405. OCLC 494791187.
- Leech, J. (1957). "A problem on strings of beads". Math. Gazette. 41: 277–278. doi:10.1017/S0025557200236115. Zbl 0079.01101.
- Berstel, Jean (April 1984). "Some Recent Results on Squarefree Words". Annual Symposium on Theoretical Aspects of Computer Science. Lecture Notes in Computer Science. 166: 14–25. doi:10.1007/3-540-12920-0_2. ISBN 978-3-540-12920-2.
- Zolotov, Boris (2015). "Another Solution to the Thue Problem of Non-Repeating Words". arXiv:1505.00019 [math.CO].
- Khalyavin, Andrey (2007). "The minimal density of a letter in an infinite ternary square-free word is 883/3215" (PDF). Journal of Integer Sequences. 10 (2): 3. Bibcode:2007JIntS..10...65K.
- Ochem, Pascal (2007). "Letter frequency in infinite repetition-free words". Theoretical Computer Science. 380 (3): 388–392. doi:10.1016/j.tcs.2007.03.027. ISSN 0304-3975.
References
- Berstel, Jean; Lauve, Aaron; Reutenauer, Christophe; Saliola, Franco V. (2009). Combinatorics on words. Christoffel words and repetitions in words. CRM Monograph Series. 27. Providence, RI: American Mathematical Society. ISBN 978-0-8218-4480-9. Zbl 1161.68043.
- Lothaire, M. (1997). Combinatorics on words. Cambridge: Cambridge University Press. ISBN 978-0-521-59924-5..
- Lothaire, M. (2011). Algebraic combinatorics on words. Encyclopedia of Mathematics and Its Applications. 90. With preface by Jean Berstel and Dominique Perrin (Reprint of the 2002 hardback ed.). Cambridge University Press. ISBN 978-0-521-18071-9. Zbl 1221.68183.
- Pytheas Fogg, N. (2002). Berthé, Valérie; Ferenczi, Sébastien; Mauduit, Christian; Siegel, Anne (eds.). Substitutions in dynamics, arithmetics and combinatorics. Lecture Notes in Mathematics. 1794. Berlin: Springer-Verlag. ISBN 978-3-540-44141-0. Zbl 1014.11015.