String girdling Earth

String girdling Earth is a mathematical puzzle with a counterintuitive solution. In a common version of this puzzle, string is wrapped around the equator of a perfectly spherical Earth. This string is cut and a piece 1 metre (3 ft 3 in) in length is added in. The string is now rearranged so that it is at a uniform height above the equator. The question that is then posed is whether the gap between string and Earth will allow the passage of a car, a cat or a thin knifeblade.

Visualisation showing that the length added to the circumference (blue) is dependent only on the additional radius (red) and not the original circumference (grey)

Solution

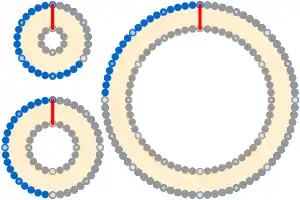
Considering that 1 metre (3 ft 3 in) is almost negligible compared with the 40,000 km (25,000 mi) circumference, the first response will be that the new position of the string will be no different from the original surface-hugging position. Surprisingly, the answer is that a cat will easily pass through the gap, the size of which will be 1/2π metres or about 16 cm (6.3 in). Even more surprising is that the size of the sphere or circle around which the string is spanned is irrelevant, and may be anything from the size of an atom to the Milky Way — the result will remain about 16 cm (6.3 in).[1]

Photograph showing the offset between starting lines of an athletics track

Let C  be the Earth's circumference, R  be its radius, c  be the added string length and r  be the added radius. As a circle of radius R  has a circumference of 2πR ,

regardless of the value of C .

A corollary is that, to raise the original string 16 cm (6.3 in) off the ground all the way around the equator, only about 1 metre (3 ft 3 in) needs to be added.

This also means that an athletics track has the same offset between starting lines on each lane, equal to 2π times the width of the lane, whether the circumference of the stadium is the standard 400 m (1,300 ft) or the size of the Milky Way.

See also
  • Visual calculus, an intuitive way to solve this type of problem, originally applied to finding the area of an annulus, given only its chord length
  • Napkin ring problem, another problem where the radius of a sphere is counter-intuitively irrelevant

References
  1. Newman, James Roy (2000). The world of mathematics, Volume 4. Courier Dover Publications. p. 2436. ISBN 0-486-41152-4., p. 2436
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.