Viète's formula

At the time Viète published his formula, methods for approximating ${\displaystyle \pi }$ to (in principle) arbitrary accuracy had long been known. Viète's own method can be interpreted as a variation of an idea of Archimedes of approximating the circumference of a circle by the perimeter of a many-sided polygon,[1] used by Archimedes to find the approximation

${\displaystyle {\frac {223}{71}}<\pi <{\frac {22}{7}}.}$

However, by publishing his method as a mathematical formula, Viète formulated the first instance of an infinite product known in mathematics,[2][3] and the first example of an explicit formula for the exact value of ${\displaystyle \pi }$.[4][5] As the first formula representing a number as the result of an infinite process rather than of a finite calculation, Viète's formula has been noted as the beginning of mathematical analysis[6] and even more broadly as "the dawn of modern mathematics".[7]

Using his formula, Viète calculated ${\displaystyle \pi }$ to an accuracy of nine decimal digits.[8] However, this was not the most accurate approximation to ${\displaystyle \pi }$ known at the time, as the Persian mathematician Jamshīd al-Kāshī had calculated ${\displaystyle \pi }$ to an accuracy of nine sexagesimal digits and 16 decimal digits in 1424.[7] Not long after Viète published his formula, Ludolph van Ceulen used a closely related method to calculate 35 digits of ${\displaystyle \pi }$, which were published only after van Ceulen's death in 1610.[7]

Viète's formula may be rewritten and understood as a limit expression

${\displaystyle \lim _{n\rightarrow \infty }\prod _{i=1}^{n}{\frac {a_{i}}{2}}={\frac {2}{\pi }}}$

where ${\displaystyle a_{n}={\sqrt {2+a_{n-1}}}}$, with initial condition ${\displaystyle a_{1}={\sqrt {2}}}$.[9] Viète did his work long before the concepts of limits and rigorous proofs of convergence were developed in mathematics; the first proof that this limit exists was not given until the work of Ferdinand Rudio in 1891.[1][10]

Comparison of the convergence of Viète's formula (×) and several historical infinite series for ${\displaystyle \pi }$. ${\displaystyle S_{n}}$ is the approximation after taking ${\displaystyle n}$ terms. Each subsequent subplot magnifies the shaded area horizontally by 10 times.

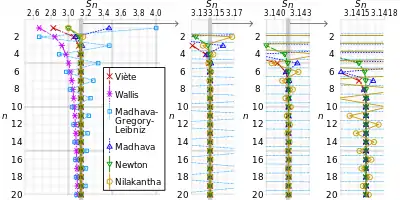
The rate of convergence of a limit governs the number of terms of the expression needed to achieve a given number of digits of accuracy. In the case of Viète's formula, there is a linear relation between the number of terms and the number of digits: the product of the first ${\displaystyle n}$ terms in the limit gives an expression for ${\displaystyle \pi }$ that is accurate to approximately ${\displaystyle 0.6n}$ digits.[8][11] This convergence rate compares very favorably with the Wallis product, a later infinite product formula for ${\displaystyle \pi }$. Although Viète himself used his formula to calculate ${\displaystyle \pi }$ only with nine-digit accuracy, an accelerated version of his formula has been used to calculate ${\displaystyle \pi }$ to hundreds of thousands of digits.[8]

Viète's formula may be obtained as a special case of a formula given more than a century later by Leonhard Euler, who discovered that:

${\displaystyle {\frac {\sin x}{x}}=\cos {\frac {x}{2}}\cdot \cos {\frac {x}{4}}\cdot \cos {\frac {x}{8}}\cdots }$

Substituting ${\displaystyle x={\frac {\pi }{2}}}$ in this formula yields:

${\displaystyle {\frac {2}{\pi }}=\cos {\frac {\pi }{4}}\cdot \cos {\frac {\pi }{8}}\cdot \cos {\frac {\pi }{16}}\cdots }$

Then, expressing each term of the product on the right as a function of earlier terms using the half-angle formula:

${\displaystyle \cos {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{2}}}}$

gives Viète's formula.[1]

It is also possible to derive from Viète's formula a related formula for ${\displaystyle \pi }$ that still involves nested square roots of two, but uses only one multiplication:[12]

${\displaystyle \pi =\lim _{k\to \infty }2^{k}\underbrace {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}}}}} _{k\ \mathrm {square} \ \mathrm {roots} },}$

which can be rewritten compactly as

${\displaystyle \pi =\displaystyle \lim _{k\to \infty }2^{k}{\sqrt {2-a_{k}}},\,a_{1}=0,\,a_{k}={\sqrt {2+a_{k-1}}}.}$

Many formulae similar to Viète's involving either nested radicals or infinite products of trigonometric functions are now known for ${\displaystyle \pi }$ and other constants such as the golden ratio.[3][12][13][14][15][16][17][18]

A sequence of regular polygons with numbers of sides equal to powers of two, inscribed in a circle. The ratios between areas or perimeters of consecutive polygons in the sequence give the terms of Viète's formula.

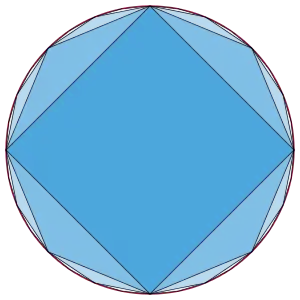
Viète obtained his formula by comparing the areas of regular polygons with ${\displaystyle 2^{n}}$ and ${\displaystyle 2^{n+1}}$ sides inscribed in a circle.[1][6] The first term in the product, √2/2, is the ratio of areas of a square and an octagon, the second term is the ratio of areas of an octagon and a hexadecagon, etc. Thus, the product telescopes to give the ratio of areas of a square (the initial polygon in the sequence) to a circle (the limiting case of a ${\displaystyle 2^{n}}$-gon). Alternatively, the terms in the product may be instead interpreted as ratios of perimeters of the same sequence of polygons, starting with the ratio of perimeters of a digon (the diameter of the circle, counted twice) and a square, the ratio of perimeters of a square and an octagon, etc.[19]

Another derivation is possible based on trigonometric identities and Euler's formula. By repeatedly applying the double-angle formula

${\displaystyle \sin x=2\sin {\frac {x}{2}}\cos {\frac {x}{2}},}$

one may prove by mathematical induction that, for all positive integers ${\displaystyle n}$,

${\displaystyle \sin x=2^{n}\sin {\frac {x}{2^{n}}}\left(\prod _{i=1}^{n}\cos {\frac {x}{2^{i}}}\right).}$

The term ${\displaystyle 2^{n}\sin {\tfrac {x}{2^{n}}}}$ goes to ${\displaystyle x}$ in the limit as ${\displaystyle n}$ goes to infinity, from which Euler's formula follows. Viète's formula may be obtained from this formula by the substitution ${\displaystyle x=\pi /2}$.[4]

• Viète's Variorum de rebus mathematicis responsorum, liber VIII (1593) on Google Books. The formula is on the second half of p. 30.