Voronoi pole
In geometry, the positive and negative Voronoi poles of a cell in a Voronoi diagram are certain vertices of the diagram.
Definition
Let be the Voronoi diagram for a set of sites , and let be the Voronoi cell of corresponding to a site . If is bounded, then its positive pole is the vertex of the boundary of that has maximal distance to the point . If the cell is unbounded, then a positive pole is not defined.
Furthermore, let be the vector from to the positive pole, or, if the cell is unbounded, let be a vector in the average direction of all unbounded Voronoi edges of the cell. The negative pole is then the Voronoi vertex in with the largest distance to such that the vector and the vector from to make an angle larger than .
Example
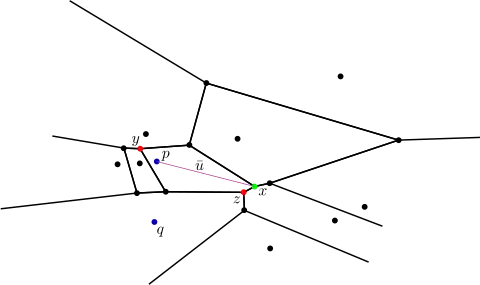
Here is the positive pole of and its negative. As the cell corresponding to is unbounded only the negative pole exists.