Wake-sleep algorithm
The wake-sleep algorithm[1] is an unsupervised learning algorithm for a stochastic multilayer neural network. The algorithm adjusts the parameters so as to produce a good density estimator.[2] There are two learning phases, the “wake” phase and the “sleep” phase, which are performed alternately.[3] It was first designed as a model for brain functioning using variational Bayesian learning. After that, the algorithm was adapted to machine learning. It can be viewed as a way to train a Helmholtz Machine.[4][5] It can also be used in Deep Belief Networks (DBN).
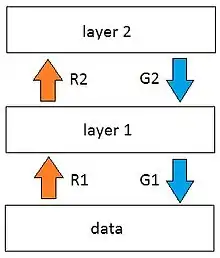
Description
The wake-sleep algorithm is visualized as a stack of layers containing representations of data.[6] Layers above represent data from the layer below it. Actual data is placed below the bottom layer, causing layers on top of it to become gradually more abstract. Between each pair of layers there is a recognition weight and generative weight, which are trained to improve reliability during the algorithm runtime.[7]
The wake-sleep algorithm is convergent[8] and can be stochastic[9] if alternated appropriately.
Training
Training consists of two phases – the “wake” phase and the “sleep” phase.
The "wake" phase
Neurons are fired by recognition connections (from what would be input to what would be output). Generative connections (leading from outputs to inputs) are then modified to increase probability that they would recreate the correct activity in the layer below – closer to actual data from sensory input.[10]
The "sleep" phase
The process is reversed in the “sleep” phase – neurons are fired by generative connections while recognition connections are being modified to increase probability that they would recreate the correct activity in the layer above – further to actual data from sensory input.[11]
Potential risks
Variational Bayesian learning is based on probabilities. There is a chance that an approximation is performed with mistakes, damaging further data representations. Another downside pertains to complicated or corrupted data samples, making it difficult to infer a representational pattern.
The wake-sleep algorithm has been suggested not to be powerful enough for the layers of the inference network in order to recover a good estimator of the posterior distribution of latent variables.[12]
See also
- Restricted Boltzmann machine, a type of neural net that is trained with a conceptually similar algorithm.
- Helmholtz machine, a neural network model trained by the wake-sleep algorithm.
References
- Hinton, Geoffrey E.; Dayan, Peter; Frey, Brendan J.; Neal, Radford (1995-05-26). "The wake-sleep algorithm for unsupervised neural networks". Science. 268 (5214): 1158–1161. Bibcode:1995Sci...268.1158H. doi:10.1126/science.7761831. PMID 7761831. S2CID 871473.
- Frey, Brendan J.; Hinton, Geoffrey E.; Dayan, Peter (1996-05-01). "Does the wake-sleep algorithm produce good density estimators?" (PDF). Advances in Neural Information Processing Systems.
- Katayama, Katsuki; Ando, Masataka; Horiguchi, Tsuyoshi (2004-04-01). "Models of MT and MST areas using wake–sleep algorithm". Neural Networks. 17 (3): 339–351. doi:10.1016/j.neunet.2003.07.004. PMID 15037352.
- Hinton, Geoffrey E.; Dayan, Peter; Frey, Brendan J.; Neal, Radford (1995-05-26). "The wake-sleep algorithm for unsupervised neural networks". Science. 268 (5214): 1158–1161. Bibcode:1995Sci...268.1158H. doi:10.1126/science.7761831. PMID 7761831. S2CID 871473.
- Dayan, Peter; Hinton, Geoffrey E. (1996-11-01). "Varieties of Helmholtz Machine". Neural Networks. Four Major Hypotheses in Neuroscience. 9 (8): 1385–1403. CiteSeerX 10.1.1.29.1677. doi:10.1016/S0893-6080(96)00009-3. PMID 12662541.
- Maei, Hamid Reza (2007-01-25). "Wake-sleep algorithm for representational learning". University of Montreal. Retrieved 2011-11-01.
- Neal, Radford M.; Dayan, Peter (1996-11-24). "Factor Analysis Using Delta Rules Wake-Sleep Learning" (PDF). University of Toronto. Retrieved 2015-11-01.
- Ikeda, Shiro; Amari, Shun-ichi; Nakahara, Hiroyuki. "Convergence of The Wake-Sleep Algorithm" (PDF). The Institute of Statistical Mathematics. Retrieved 2015-11-01.
- Dalzell, R.W.H.; Murray, A.F. (1999-01-01). "A framework for a discrete valued Helmholtz machine". 9th International Conference on Artificial Neural Networks: ICANN '99. 1. pp. 49–54 vol.1. doi:10.1049/cp:19991083. ISBN 0-85296-721-7.
- Hinton, Geoffrey; Dayan, Peter; Frey, Brendan J; Neal, Radford M (1995-04-03). "The wake-sleep algorithm for unsupervised neural networks" (PDF). PMID 7761831. Retrieved 2015-11-01. Cite journal requires
|journal=(help) - Dayan, Peter. "Helmholtz Machines and Wake-Sleep Learning" (PDF). Retrieved 2015-11-01.
- Bornschein, Jörg; Bengio, Yoshua (2014-06-10). "Reweighted Wake-Sleep". arXiv:1406.2751 [cs.LG].