Aggregated distribution
An aggregated distribution, commonly found among predators and parasites, is a highly uneven (skewed) statistical distribution pattern in which they collect or aggregate in regions, which may be widely separated, where their prey or hosts are at high density. This distribution makes sampling difficult and invalidates commonly-used parametric statistics. A similar pattern is found among predators that search for their prey.[1]
In predators
When predators need to search for their prey, they could search at random, as has been assumed in models such as those made by Lotka in 1925 and Volterra in 1928. This would imply that they scatter themselves evenly across the environment.[1] However, prey may be concentrated at high densities in some areas and scarce elsewhere. The zoologists M. P. Hassell and R. M. May noted that predators and parasites, too, might aggregate themselves where prey was abundant, choosing some response curve: they observed for example that redshanks (predatory birds) adopted a sigmoid (s-shaped) response to the density of Corophium (amphipod) prey per square metre of mudflats. They noted, too, that several different behaviours of predators or parasites could cause them to aggregate selectively in areas where prey are at high density: they could be attracted by a volatile substance liberated by prey or the plants they are feeding on; they could choose to spend more time in areas where they have caught prey, as many predators appear to do; or, predators could follow an individual predator which had located prey, as is seen in feeding terns. Aggregated distributions of predators where they tend to spend time in areas where prey are concentrated have the effect of stabilising prey populations; when the time to travel between such concentrated areas is high; and when the prey populations too are more highly clumped.[1]
In parasites
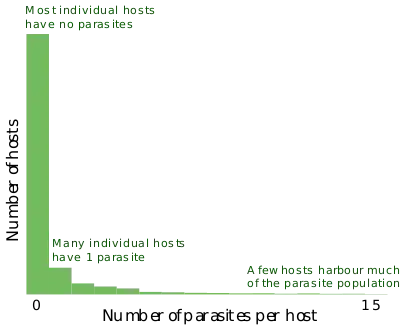
Parasite aggregation with respect to hosts is, according to Robert Poulin "a defining feature of metazoan parasite populations."[2] The main reason for this is probably either that some hosts are more exposed to parasites, or that they are more susceptible to them.[2] Aggregation is seen in directly transmitted parasites (those not using a vector) from many groups: ectoparasites like lice and mites, marine parasites like copepods and cyamid amphipods, and many kinds of nematode, fungi, protozoa, bacteria, and viruses. It is widespread, too, in trophically transmitted parasites of animals. The observed pattern is that most individual hosts are free or almost free of parasites, while a minority carry a large number of parasites.[3]
Quantitative ecology
Aggregated distribution of parasites across their hosts poses considerable problems for students of parasite ecology, as it renders parametric statistics as commonly used by biologists invalid. Log-transformation of data before the application of parametric test, or the use of non-parametric statistics is recommended by several authors, but this can give rise to further problems, so quantitative parasitology is based on more advanced biostatistical methods.[4]
References
- Hassell, M. P.; May, R. M. (June 1974). "Aggregation of Predators and Insect Parasites and its Effect on Stability". Journal of Animal Ecology. 43 (2): 567–594. JSTOR 3384.
- Poulin, Robert (January 2013). "Explaining variability in parasite aggregation levels among host samples". Parasitology. 140 (04): 541–546. doi:10.1017/s0031182012002053.
- Poulin, Robert; Randhawa, Haseeb S. (February 2015). "Evolution of parasitism along convergent lines: from ecology to genomics". Parasitology. 142 (Suppl 1): S6–S15. doi:10.1017/S0031182013001674. PMC 4413784. PMID 24229807.
- Rózsa, L.; Reiczigel, J.; Majoros, G. (2000). "Quantifying parasites in samples of hosts". J. Parasitol. 86 (2): 228–32. doi:10.1645/0022-3395(2000)086[0228:QPISOH]2.0.CO;2. PMID 10780537.
