Bifolium

A bifolium is a quartic plane curve with equation in Cartesian coordinates:

For other uses, see Bifolium (disambiguation).
Bifolium with a = 1

Construction and equations
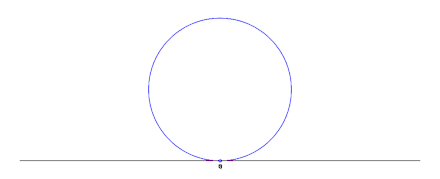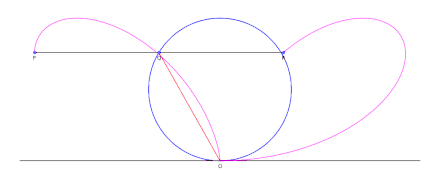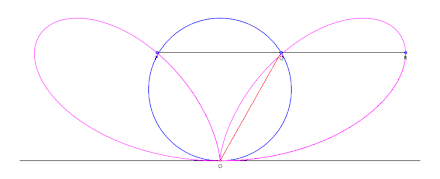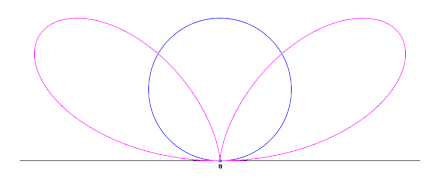
Construction of the bifolium

Given a circle C through a point O, and line L tangent to the circle at point O: for each point Q on C, define the point P such that PQ is parallel to the tangent line L, and PQ = OQ. The collection of points P forms the bifolium.[1]

In polar coordinates, the bifolium's equation is

For a = 1, the total included area is approximately 0.10.

References
  1. Kokoska, Stephen. "Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers" (PDF). Retrieved 6 January 2018.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.