Borromean rings

In mathematics, the Borromean rings consist of three topological circles which are linked but where removing any one ring leaves the other two unconnected. In other words, no two of the three rings are linked with each other as a Hopf link, but nonetheless all three are linked. The Borromean rings are one of a class of such links called Brunnian links.

Borromean rings
L6a4
Braid length6
Braid no.3
Crossing no.6
Hyperbolic volume7.327724753
Stick no.9
Unknotting no.2
Conway notation[.1]
A-B notation63
2
ThistlethwaiteL6a4
Last /NextL6a3 / L6a5
Other
alternating, hyperbolic

Name and history
Valknut on Stora Hammars I stone

The name "Borromean rings" comes from their use in the coat of arms of the aristocratic Borromeo family in Northern Italy.[1] The link itself is much older and has appeared in the form of the valknut, three linked equilateral triangles with parallel sides, on Norse image stones dating back to the 7th century.[2] A stone pillar in the 6th-century Marundeeswarar Temple in India shows the Borromean rings in another form, three linked equilateral triangles rotated from each other to form a regular enneagram.[3] The Ōmiwa Shrine in Japan is also decorated with a motif of the Borromean rings, in their conventional circular form.[4]

The Borromean rings as a symbol of the Christian Trinity, from a 13th-century manuscript.

The Borromean rings have been used in different contexts to indicate strength in unity.[5] In particular, some have used the design to symbolize the Trinity.[6] The psychoanalyst Jacques Lacan found inspiration in the Borromean rings as a model for his topology of human subjectivity, with each ring representing a fundamental Lacanian component of reality (the "real", the "imaginary", and the "symbolic").[7]

The rings were used as the logo of Ballantine beer, and are still used by the Ballantine brand beer, now distributed by the current brand owner, the Pabst Brewing Company.[8][9] For this reason they have sometimes been called the "Ballantine rings".[6][8]

Seifert surfaces for the Borromean rings were featured by Martin Gardner in his September 1961 "Mathematical Games column" in Scientific American.[9] In 2006, the International Mathematical Union decided at the 25th International Congress of Mathematicians in Madrid, Spain to use a new logo based on the Borromean rings.[4]

Partial and multiple rings
A monkey's fist knot

In medieval and renaissance Europe, a number of visual signs consist of three elements interlaced together in the same way that the Borromean rings are shown interlaced (in their conventional two-dimensional depiction), but with individual elements that are not closed loops. Examples of such symbols are the Snoldelev stone horns[10] and the Diana of Poitiers crescents.[6]

Similarly, a monkey's fist knot is essentially a 3-dimensional representation of the Borromean rings, albeit with three layers, in most cases.[11]

The Discordian "mandala", containing five Borromean rings configurations

Some knot-theoretic links contain multiple Borromean rings configurations; one five-loop link of this type is used as a symbol in Discordianism, based on a depiction in the Principia Discordia.[12]

Physical realizations
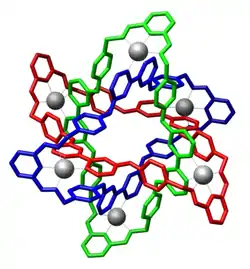
Crystal structure of molecular Borromean rings reported by Stoddart et al. (Science 2004)[13]

Molecular Borromean rings are the molecular counterparts of Borromean rings, which are mechanically-interlocked molecular architectures. In 1997, biologist Chengde Mao and coworkers of New York University succeeded in constructing a set of rings from DNA.[14] In 2003, chemist Fraser Stoddart and coworkers at UCLA utilised coordination chemistry to construct a set of rings in one step from 18 components.[13] Borromean ring structures have been shown to be an effective way to represent the structure of certain atomically precise noble metal clusters which are shielded by a surface layer of thiolate ligands (-SR), such as Au25(SR)18 and Ag25(SR)18.[15] A library of Borromean networks has been synthesized by design by Giuseppe Resnati and coworkers via halogen bond driven self-assembly.[16] In order to access the molecular Borromean ring consisting of three unequal cycles a step-by-step synthesis was proposed by Jay S. Siegel and coworkers.[17]

A quantum-mechanical analog of Borromean rings is called a halo state or an Efimov state (the existence of such states was predicted by physicist Vitaly Efimov, in 1970). For the first time the research group of Rudolf Grimm and Hanns-Christoph Nägerl from the Institute for Experimental Physics (University of Innsbruck, Austria) experimentally confirmed such a state in an ultracold gas of caesium atoms in 2006, and published their findings in the scientific journal Nature.[18] A team of physicists led by Randall Hulet of Rice University in Houston achieved this with a set of three bound lithium atoms and published their findings in the online journal Science Express.[19] In 2010, a team led by K. Tanaka created an Efimov state within a nucleus.[20]

Mathematical properties

Ring shape
Unsolved problem in mathematics:
Are there three unknotted curves, not all circles, that cannot form the Borromean rings?
(more unsolved problems in mathematics)

The Borromean rings are typically drawn with their rings projecting to circles in the plane of the drawing, but three-dimensional circular Borromean rings are an impossible object: it is not possible to form the Borromean rings from circles in three-dimensional space.[21] Michael H. Freedman and Richard Skora (1987) proved that a certain class of links, including the Borromean links, cannot be exactly circular.[22] For three rings in their conventional Borromean arrangement, this can be seen from considering the link diagram. If one assumes that two of the circles touch at their two crossing points, then they lie in either a plane or a sphere. In either case, the third circle must pass through this plane or sphere four times, without lying in it, which is impossible.[23]

Realization of Borromean rings using ellipses

However, the Borromean rings can be realized using ellipses.[4] These may be taken to be of arbitrarily small eccentricity; i.e. no matter how close to being circular their shape may be, as long as they are not perfectly circular, they can form Borromean links if suitably positioned.

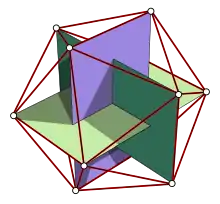
Three linked golden rectangles in a regular icosahedron

A realization of the Borromean rings by three mutually perpendicular golden rectangles can be found within a regular icosahedron by connecting three opposite pairs of its edges.[4]

Every three unknotted polygons in Euclidean space may be combined, after a suitable scaling transformation, to form the Borromean rings. If all three polygons are planar, then scaling is not needed. More generally, Matthew Cook has conjectured that any three unknotted simple closed curves in space, not all circles, can be combined without scaling to form the Borromean rings. After Jason Cantarella suggested a possible counterexample, Hugh Nelson Howards weakened the conjecture to apply to any three planar curves that are not all circles. On the other hand, although there are infinitely many Brunnian links with three links, the Borromean rings are the only one that can be formed from three convex curves.[24]

Linkedness

In knot theory, the Borromean rings are a simple example of a Brunnian link: although each pair of rings is unlinked, the whole link cannot be unlinked. There are a number of ways of seeing that the Borromean rings are linked; one is to count their Fox n-colorings. A trivial link would have 125 Fox 5-colorings (one for each choice of color for each of the three links), but the Borromean rings have only five.[21]

Number theory

In arithmetic topology, there is an analogy between knots and prime numbers in which one considers links between primes. The triple of primes (13, 61, 937) are linked modulo 2 (the Rédei symbol is −1) but are pairwise unlinked modulo 2 (the Legendre symbols are all 1). Therefore, these primes have been called a "proper Borromean triple modulo 2"[25] or "mod 2 Borromean primes".[26]

Hyperbolic geometry

The Borromean rings are a hyperbolic link: the complement of the Borromean rings in the 3-sphere admits a complete hyperbolic metric of finite volume. The canonical (Epstein–Penner) polyhedral decomposition of the complement consists of two ideal regular octahedra. The volume is where is the Lobachevsky function.[27] This was a central example in the video Not Knot about knot complements, produced in 1991 by the Geometry Center.[28]

See also

References
  1. Schoeck, Richard J. (Spring 1968), "Mathematics and the languages of literary criticism", The Journal of Aesthetics and Art Criticism, 26 (3): 367–376, doi:10.2307/429121, JSTOR 429121
  2. Bruns, Carson J.; Stoddart, J. Fraser (2011), "The mechanical bond: A work of art", in Fabbrizzi, L. (ed.), Beauty in Chemistry, Topics in Current Chemistry, 323, Springer-Verlag, pp. 19–72, doi:10.1007/128_2011_296
  3. Lakshminarayan, Arul (May 2007), "Borromean triangles and prime knots in an ancient temple", Resonance, 12 (5): 41–47, doi:10.1007/s12045-007-0049-7
  4. Gunn, Charles; Sullivan, John M. (2008), "The Borromean Rings: A video about the New IMU logo", in Sarhangi, Reza; Séquin, Carlo H. (eds.), Bridges Leeuwarden: Mathematics, Music, Art, Architecture, Culture, London: Tarquin Publications, pp. 63–70, ISBN 9780966520194
  5. Aravind, P. K. (1997), "Borromean Entanglement of the GHZ State" (PDF), in Cohen, R. S.; Horne, M.; Stachel, J. (eds.), Potentiality, Entanglement and Passion-at-a-Distance, Boston Studies in the Philosophy of Science, Springer, pp. 53–59, doi:10.1007/978-94-017-2732-7_4, they represent the motto 'united we stand, divided we fall', since if one of the rings is cut the other two fall apart
  6. Cromwell, Peter; Beltrami, Elisabetta; Rampichini, Marta (March 1998), "The Borromean rings", The mathematical tourist, The Mathematical Intelligencer, 20 (1): 53–62, doi:10.1007/bf03024401; see in particular "Circles in Trinitarian Iconography", pp. 58–59
  7. Ragland-Sullivan, Ellie; Milovanovic, Dragan (2004), "Introduction: Topologically Speaking", Lacan: Topologically Speaking, Other Press, ISBN 9781892746764
  8. Glick, Ned (September 1999), "The 3-ring symbol of Ballantine Beer", The mathematical tourist, The Mathematical Intelligencer, 21 (4): 15–16, doi:10.1007/bf03025332
  9. Gardner, Martin (September 1961), "Surfaces with edges linked in the same way as the three rings of a well-known design", Mathematical Games, Scientific American; reprinted as Gardner, Martin (1991), "Knots and Borromean Rings", The Unexpected Hanging and Other Mathematical Diversions, University of Chicago Press, pp. 24–33
  10. Baird, Joseph L. (1970), "Unferth the þyle", Medium Ævum, 39 (1): 1–12, doi:10.2307/43631234, JSTOR 43631234, the stone bears also representations of three horns interlaced
  11. Ashley, Clifford Warren (1993) [1944], The Ashley Book of Knots, Doubleday, p. 354
  12. "Mandala", Principia Discordia (4th ed.), March 1970, p. 43
  13. Kelly S. Chichak; Stuart J. Cantrill; Anthony R. Pease; Sheng-Hsien Chiu; Gareth W. V. Cave; Jerry L. Atwood; J. Fraser Stoddart (28 May 2004), "Molecular Borromean Rings" (PDF), Science, 304 (5675): 1308–1312, Bibcode:2004Sci...304.1308C, doi:10.1126/science.1096914, PMID 15166376
  14. C. Mao; W. Sun; N. C. Seeman (1997), "Assembly of Borromean rings from DNA", Nature, 386 (6621): 137–138, Bibcode:1997Natur.386..137M, doi:10.1038/386137b0, PMID 9062186
  15. Natarajan, Ganapati; Mathew, Ammu; Negishi, Yuichi; Whetten, Robert L.; Pradeep, Thalappil (2015-12-02), "A Unified Framework for Understanding the Structure and Modifications of Atomically Precise Monolayer Protected Gold Clusters", The Journal of Physical Chemistry C, 119 (49): 27768–27785, doi:10.1021/acs.jpcc.5b08193, ISSN 1932-7447
  16. Vijith Kumar; Tullio Pilati; Giancarlo Terraneo; Franck Meyer; Pierangelo Metrangolo; Giuseppe Resnati (2017), "Halogen bonded Borromean networks by design: topology invariance and metric tuning in a library of multi-component systems", Chemical Science, 8 (3): 1801–1810, doi:10.1039/C6SC04478F, PMC 5477818, PMID 28694953
  17. Veliks, Janis; Seifert, Helen M.; Frantz, Derik K.; Klosterman, Jeremy K.; Tseng, Jui-Chang; Linden, Anthony; Siegel, Jay S. (2016), "Towards the molecular Borromean link with three unequal rings: double-threaded ruthenium(ii) ring-in-ring complexes", Organic Chemistry Frontiers, 3 (6): 667–672, doi:10.1039/c6qo00025h
  18. T. Kraemer; M. Mark; P. Waldburger; J. G. Danzl; C. Chin; B. Engeser; A. D. Lange; K. Pilch; A. Jaakkola; H.-C. Nägerl; R. Grimm (2006), "Evidence for Efimov quantum states in an ultracold gas of caesium atoms", Nature, 440 (7082): 315–318, arXiv:cond-mat/0512394, Bibcode:2006Natur.440..315K, doi:10.1038/nature04626, PMID 16541068
  19. Clara Moskowitz (December 16, 2009), Strange Physical Theory Proved After Nearly 40 Years, Live Science
  20. K. Tanaka (2010), "Observation of a Large Reaction Cross Section in the Drip-Line Nucleus 22C", Physical Review Letters, 104 (6): 062701, Bibcode:2010PhRvL.104f2701T, doi:10.1103/PhysRevLett.104.062701, PMID 20366816
  21. Aigner, Martin; Ziegler, Günter M. (2018), "Chapter 15: The Borromean Rings Don't Exist", Proofs from THE BOOK (6th ed.), Springer, pp. 99–106, doi:10.1007/978-3-662-57265-8_15, ISBN 978-3-662-57265-8
  22. Freedman, Michael H.; Skora, Richard (1987), "Strange Actions of Groups on Spheres", Journal of Differential Geometry, 25: 75–98, doi:10.4310/jdg/1214440725
  23. Lindström, Bernt; Zetterström, Hans-Olov (1991), "Borromean Circles are Impossible", American Mathematical Monthly, 98 (4): 340–341, doi:10.2307/2323803, JSTOR 2323803. Note however that Gunn & Sullivan (2008) write that this reference "seems to incorrectly deal only with the case that the three-dimensional configuration has a projection homeomorphic to" the conventional three-circle drawing of the link.
  24. Howards, Hugh Nelson (2013), "Forming the Borromean rings out of arbitrary polygonal unknots", Journal of Knot Theory and its Ramifications, 22 (14): 1350083, 15, arXiv:1406.3370, doi:10.1142/S0218216513500831, MR 3190121
  25. Vogel, Denis (2005), Masseyprodukte in der Galoiskohomologie von Zahlkörpern [Massey products in the Galois cohomology of number fields], Mathematisches Institut, Georg-August-Universität Göttingen: Seminars Winter Term 2004/2005, Göttingen: Universitätsdrucke Göttingen, pp. 93–98, doi:10.11588/heidok.00004418, MR 2206880
  26. Morishita, Masanori (22 April 2009), Analogies between Knots and Primes, 3-Manifolds and Number Rings, arXiv:0904.3399, Bibcode:2009arXiv0904.3399M
  27. William Thurston (March 2002), "7. Computation of volume" (PDF), The Geometry and Topology of Three-Manifolds, p. 165
  28. Abbott, Steve (July 1997), "Review of Not Knot and Supplement to Not Knot", The Mathematical Gazette, 81 (491): 340–342, doi:10.2307/3619248, JSTOR 3619248
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.