Calabi triangle

The Calabi triangle is a special triangle found by Eugenio Calabi and defined by its property of having three different placements for the largest square that it contains.[1] It is an obtuse isosceles triangle with an irrational but algebraic ratio between the lengths of its sides and its base.

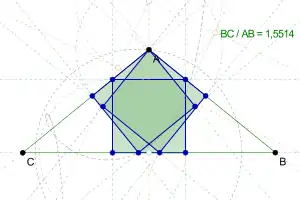
Definition

Consider the largest square that can be placed in an arbitrary triangle. It may be that such a square could be positioned in the triangle in more than one way. If the largest such square can be positioned in three different ways, then the triangle is either an equilateral triangle or the Calabi triangle.[2][3] Thus, the Calabi triangle may be defined as a triangle that is not equilateral and has three placements for its largest square.

Shape

The Calabi triangle is isosceles. The ratio of the base to either leg is

which approximates to 1.55138752454. In terms of trigonometric functions, it is

It is the largest positive root of

and has continued fraction representation [1, 1, 1, 4, 2, 1, 2, 1, 5, 2, 1, 3, 1, 1, 390, ...].[2]

The Calabi triangle is obtuse with base angles 39.1320261...° and third angle 101.7359477...°.

See also

References
  1. Eugenio Calabi (3 Nov 1997). "Outline of Proof Regarding Squares Wedged in Triangle". Archived from the original on 12 December 2012. Retrieved 3 May 2018.
  2. Calabi's triangle at Mathworld
  3. Conway, J.H.; Guy, R.K. (1996). "Calabi's Triangle". The Book of Numbers. New York: Springer-Verlag. p. 206.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.