Central binomial coefficient
In mathematics the nth central binomial coefficient is the particular binomial coefficient
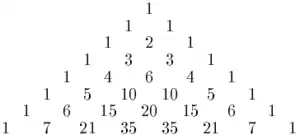
They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:
Properties
The central binomial coefficients satisfy the recurrence
Since we find
Together with the binomial series we obtain the generating function
and exponential generating function
where I0 is a modified Bessel function of the first kind.[1]
The Wallis product can be written in asymptotic form for the central binomial coefficient:
The latter can also be easily established by means of Stirling's formula. On the other hand, it can also be used as a means to determine the constant in front of the Stirling formula, by comparison.
Simple bounds that immediately follow from are
Some better bounds are[2]
and, if more accuracy is required,
- for all
The only central binomial coefficient that is odd is 1. More specifically, the number of factors of 2 in is equal to the number of ones in the binary representation of n.[3] Half the central binomial coefficient (for ) (sequence A001700 in the OEIS) is seen in Wolstenholme's theorem.
By the Erdős squarefree conjecture, proven in 1996, no central binomial coefficient with n > 4 is squarefree.
The central binomial coefficient equals the sum of the squares of the elements in row n of Pascal's triangle.[1]
Related sequences
The closely related Catalan numbers Cn are given by:
A slight generalization of central binomial coefficients is to take them as , with appropriate real numbers n, where is the gamma function and is the beta function.
The powers of two that divide the central binomial coefficients are given by Gould's sequence, whose nth element is the number of odd integers in row n of Pascal's triangle.
References
- Sloane, N. J. A. (ed.). "Sequence A000984 (Central binomial coefficients)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Kazarinoff, N.D. Geometric inequalities, New York: Random House, 1961
- Sloane, N. J. A. (ed.). "Sequence A000120". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Koshy, Thomas (2008), Catalan Numbers with Applications, Oxford University Press, ISBN 978-0-19533-454-8.
External links
- Central binomial coefficient at PlanetMath.
- Binomial coefficient at PlanetMath.
- Pascal's triangle at PlanetMath.
- Catalan numbers at PlanetMath.
This article incorporates material from Central binomial coefficient on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
