Chromatic scale

The chromatic scale is the set of twelve pitches, each pair separated by the interval of a semitone, used in tonal music. Almost all western musical instruments, such as the piano, are made to produce the chromatic scale, while other instruments, such as the horn, trombone, and violin can also produce microtones, or notes between those available on a piano.

Chromatic scale: every key of one octave on the piano keyboard

Most music uses a subset of the chromatic scale, such as heptatonic scales, characteristically diatonic, and seldom the entire chromatic scale. These scales use notes which are selected based on an interval pattern. While the chromatic scale is fundamental in western music theory, it is seldom directly used in its entirety in musical compositions or improvisation.

Structure

Essentially, the chromatic scale uses a sound's fundamental frequency and its harmonics to define a single note, that is, a group of similar sounds. The twelve notes are defined to lie within the lowest note's frequency and its first harmonic, called an octave, and populates the aural space in that range. For each octave, a similar population and aural interval between notes is maintained. This enables the chromatic scale to describe all the notes within (and outside) the human hearing range.

Musical instruments need to be adjusted so they play the same pitch as other instruments, regardless of note and frequency. This adjustment is known as tuning the instrument. Although the chromatic scale only defines twelve notes, these are also used to tune an instrument's additional notes, such as a piano's 88 keys. Instead of defining the fundamental frequencies for each note, tuning systems rely on a single frequency assigned to a note and a method of deriving all other notes from that. The method of tuning is called the temperament. The actual note and tuning frequency may also vary. The chromatic scale enables instruments to be independently tuned to the same or transposed frequencies of other instruments. Tuning doesn't drop or add notes to the chromatic scale.

Formal definition

The chromatic scale or twelve-tone scale is a musical scale with twelve pitches, each a semitone, also known as a half-step, above or below its adjacent pitches. As a result, in 12-tone equal temperament (the most common tuning in Western music), the chromatic scale covers all 12 of the available pitches. Thus, there is only one chromatic scale.[lower-alpha 1]

In equal temperament, all the semitones have the same size (100 cents, and there are twelve semitones in an octave (1200 cents). As a result, the notes of an equal-tempered chromatic scale are equally-spaced.

The chromatic scale...is a series of half steps which comprises all the pitches of our [12-tone] equal-tempered system.

— Allen Forte (1979)[1]

All of the pitches in common use, considered together, constitute the chromatic scale. It is made up entirely of successive half steps, the smallest interval in Western music....Counting by half steps, an octave includes twelve different pitches, white and black keys together. The chromatic scale, then, is a collection of all the available pitches in order upward or downward, one octave's worth after another.

— Walter Piston (1987)[2]

A chromatic scale is a nondiatonic scale consisting entirely of half-step intervals. Since each tone of the scale is equidistant from the next [symmetry] it has no tonic [key].[3] ...
Chromaticism [is t]he introduction of some pitches of the chromatic scale into music that is basically diatonic in orientation, or music that is based on the chromatic scale instead of the diatonic scales.[4]

— Benward & Saker (2003)

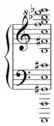
The ascending and descending chromatic scale is shown below.[3]

Chromatic scale drawn as a circle
The diatonic scale notes (above) and the non-scale chromatic notes (below)[1]

The twelve notes of the octave—all the black and white keys in one octave on the piano—form the chromatic scale. The tones of the chromatic scale (unlike those of the major or minor scale) are all the same distance apart, one half step. The word chromatic comes from the Greek chroma, color; and the traditional function of the chromatic scale is to color or embellish the tones of the major and minor scales. It does not define a key, but it gives a sense of motion and tension. It has long been used to evoke grief, loss, or sorrow. In the twentieth century it has also become independent of major and minor scales and is used as the basis for entire compositions.

— Roger Kamien (1976)[5]

Notation
The circle of fifths drawn within the chromatic circle as a star dodecagram.[6]

The chromatic scale has no set enharmonic spelling that is always used. Its spelling is, however, often dependent upon major or minor key signatures and whether the scale is ascending or descending. In general, the chromatic scale is usually notated with sharp signs when ascending and flat signs when descending. It is also notated so that no scale degree is used more than twice in succession (for instance, G♭ – G♮ – G♯).

Similarly, some notes of the chromatic scale have enharmonic equivalents in solfege. The rising scale is Do, Di, Re, Ri, Mi, Fa, Fi, Sol, Si, La, Li, Ti and the descending is Ti, Te/Ta, La, Le/Lo, Sol, Se, Fa, Mi, Me/Ma, Re, Ra, Do, However, once 0 is given to a note, due to octave equivalence, the chromatic scale may be indicated unambiguously by the numbers 0-11 mod twelve. Thus two perfect fifths are 0-7-2. Tone rows, orderings used in the twelve-tone technique, are often considered this way due to the increase ease of comparing inverse intervals and forms (inversional equivalence).

Pitch-rational tunings

Pythagorean
Main article: Pythagorean tuning

The most common conception of the chromatic scale before the 13th century was the Pythagorean chromatic scale (Play ). Due to a different tuning technique, the twelve semitones in this scale have two slightly different sizes. Thus, the scale is not perfectly symmetric. Many other tuning systems, developed in the ensuing centuries, share a similar asymmetry.

In Pythagorean tuning (i.e. 3-limit just intonation) the chromatic scale is tuned as follows, in perfect fifths from G♭ to A♯ centered on D (in bold) (G♭-D♭-A♭-E♭-B♭-F-D-G-D-A-E-B-F♯-C♯-G♯-D♯-A♯), with sharps higher than their enharmonic flats (cents rounded to one decimal):

C D♭ C♯ D E♭ D♯ E F G♭ F♯ G A♭ G♯ A B♭ A♯ B C
Pitch
ratio		 1​256⁄243​2187⁄2048​9⁄8​32⁄27​19683⁄16384​81⁄64​4⁄3​1024⁄729​729⁄512​3⁄2​128⁄81​6561⁄4096​27⁄16​16⁄9​59049⁄32768​243⁄1282
Cents 090.2113.7203.9294.1317.6407.8498588.3611.7702792.2815.6905.9996.11019.61109.81200

where ​256⁄243 is a diatonic semitone (Pythagorean limma) and ​2187⁄2048 is a chromatic semitone (Pythagorean apotome).

The chromatic scale in Pythagorean tuning can be tempered to the 17-EDO tuning (P5 = 10 steps = 705.88 cents).

Just intonation
Main article: Just intonation § Twelve-tone scale

In 5-limit just intonation the chromatic scale, Ptolemy's intense chromatic scale, is as follows, with flats higher than their enharmonic sharps, and new notes between E - F and B - C (cents rounded to one decimal):

CC♯D♭DD♯E♭EE♯/F♭FF♯G♭GG♯A♭AA♯B♭BB♯/C♭C
Pitch ratio 1​25⁄24​16⁄15​9⁄8​75⁄64​6⁄5​5⁄4​32⁄25​4⁄3​25⁄18​36⁄25​3⁄2​25⁄16​8⁄5​5⁄3​125⁄72​9⁄5​15⁄8​48⁄252
Cents 070.7111.7203.9274.6315.6386.3427.4498568.7631.3702772.6813.7884.49551017.61088.31129.31200

The fractions ​9⁄8 and ​10⁄9, ​6⁄5 and ​32⁄27, ​5⁄4 and ​81⁄64, ​4⁄3 and ​27⁄20, and many other pairs are interchangeable, as ​81⁄80 (syntonic comma) is tempered out.

Just intonation tuning can be approximated by 19-EDO tuning (P5 = 11 steps = 694.74 cents).

Non-Western cultures

The ancient Chinese chromatic scale is called Shí-èr-lǜ. However, "it should not be imagined that this gamut ever functioned as a scale, and it is erroneous to refer to the 'Chinese chromatic scale', as some Western writers have done. The series of twelve notes known as the twelve lü were simply a series of fundamental notes from which scales could be constructed."[7] However, "from the standpoint of tonal music [the chromatic scale] is not an independent scale, but derives from the diatonic scale,"[1] making the Western chromatic scale a gamut of fundamental notes from which scales could be constructed as well.

See also

Notes
  1. As every chromatic scale is identical under transposition, inversion, and retrograde to every other.

Sources
  1. Forte, Allen, Tonal Harmony, third edition (S.l.: Holt, Rinehart, and Wilson, 1979): p.4-5. ISBN 0-03-020756-8.
  2. Piston, Walter (1987/1941). Harmony, p.5. 5th edition revised by Devoto, Mark. W. W. Norton, New York/London. ISBN 0-393-95480-3.
  3. Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.37. Seventh Edition. ISBN 978-0-07-294262-0.
  4. Benward, Bruce & Saker (2003). "Glossary", p.359.
  5. Kamien, Roger (1990). Music: An Appreciation, p.44. Brief edition. McGraw-Hill. ISBN 0-07-033568-0.
  6. McCartin, Brian J. (1998). "Prelude to Musical Geometry". The College Mathematics Journal. 29 (5 (November)): 354–370. JSTOR 2687250. Archived from the original on 2008-05-17. Retrieved 2008-07-29., p.364.
  7. Needham, Joseph (1962/2004). Science and Civilization in China, Vol. IV: Physics and Physical Technology, p.170-171. ISBN 978-0-521-05802-5.

Further reading
  • Hewitt, Michael. 2013. Musical Scales of the World. The Note Tree. ISBN 978-0957547001
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.