Control table
Control tables are tables that control the control flow or play a major part in program control. There are no rigid rules about the structure or content of a control table—its qualifying attribute is its ability to direct control flow in some way through "execution" by a processor or interpreter. The design of such tables is sometimes referred to as table-driven design[1][2] (although this typically refers to generating code automatically from external tables rather than direct run-time tables). In some cases, control tables can be specific implementations of finite-state-machine-based automata-based programming. If there are several hierarchical levels of control table they may behave in a manner equivalent to UML state machines[3]
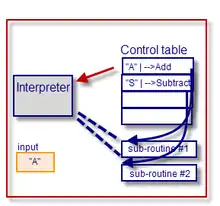
Control tables often have the equivalent of conditional expressions or function references embedded in them, usually implied by their relative column position in the association list. Control tables reduce the need for programming similar structures or program statements over and over again. The two-dimensional nature of most tables makes them easier to view and update than the one-dimensional nature of program code. In some cases, non-programmers can be assigned to maintain the control tables.
Typical usage
- Transformation of input values to:
- an index, for later branching or pointer lookup
- a program name, relative subroutine number, program label or program offset, to alter control flow
- Controlling a main loop in event-driven programming using a control variable for state transitions
- Controlling the program cycle for Online transaction processing applications
More advanced usage
- Acting as virtual instructions for a virtual machine processed by an interpreter
- similar to bytecode – but usually with operations implied by the table structure itself
Table structure
The tables can have multiple dimensions, of fixed or variable lengths and are usually portable between computer platforms, requiring only a change to the interpreter, not the algorithm itself – the logic of which is essentially embodied within the table structure and content. The structure of the table may be similar to a multimap associative array, where a data value (or combination of data values) may be mapped to one or more functions to be performed.
One-dimensional tables
In perhaps its simplest implementation, a control table may sometimes be a one-dimensional table for directly translating a raw data value to a corresponding subroutine offset, index or pointer using the raw data value either directly as the index to the array, or by performing some basic arithmetic on the data beforehand. This can be achieved in constant time (without a linear search or binary search using a typical lookup table on an associative array). In most architectures, this can be accomplished in two or three machine instructions – without any comparisons or loops. The technique is known as a "trivial hash function" or, when used specifically for branch tables, "double dispatch". For this to be feasible, the range of all possible values of the data needs to be small (e.g. an ASCII or EBCDIC character value which have a range of hexadecimal '00' – 'FF'. If the actual range is guaranteed to be smaller than this, the array can be truncated to less than 256 bytes).
Table to translate raw ASCII values (A,D,M,S) to new subroutine index (1,4,3,2) in constant time using one-dimensional array
(gaps in the range are shown as '..' for this example, meaning 'all hex values up to next row'. The first two columns are not part of the array)
| ASCII | Hex | Array |
|---|---|---|
| null | 00 | 00 |
| .. | .. | 00 |
| @ | 40 | 00 |
| A | 41 | 01 |
| .. | .. | 00 |
| D | 44 | 04 |
| .. | .. | 00 |
| M | 4D | 03 |
| .. | .. | 00 |
| S | 53 | 02 |
In automata-based programming and pseudoconversational transaction processing, if the number of distinct program states is small, a "dense sequence" control variable can be used to efficiently dictate the entire flow of the main program loop.
A two byte raw data value would require a minimum table size of 65,536 bytes – to handle all input possibilities – whilst allowing just 256 different output values. However, this direct translation technique provides an extremely fast validation & conversion to a (relative) subroutine pointer if the heuristics, together with sufficient fast access memory, permits its use.
Branch tables
A branch table is a one-dimensional 'array' of contiguous machine code branch/jump instructions to effect a multiway branch to a program label when branched into by an immediately preceding, and indexed branch. It is sometimes generated by an optimizing compiler to execute a switch statement – provided that the input range is small and dense, with few gaps (as created by the previous array example) .
Although quite compact – compared to the multiple equivalent If statements – the branch instructions still carry some redundancy, since the branch opcode and condition code mask are repeated alongside the branch offsets. Control tables containing only the offsets to the program labels can be constructed to overcome this redundancy (at least in assembly languages) and yet requiring only minor execution time overhead compared to a conventional branch table.
Multi-dimensional tables
More usually, a control table can be thought of as a Truth table or as an executable ("binary") implementation of a printed decision table (or a tree of decision tables, at several levels). They contain (often implied) propositions, together with one or more associated 'actions'. These actions are usually performed by generic or custom-built subroutines that are called by an "interpreter" program. The interpreter in this instance effectively functions as a virtual machine, that 'executes' the control table entries and thus provides a higher level of abstraction than the underlying code of the interpreter.
A control table can be constructed along similar lines to a language dependent switch statement but with the added possibility of testing for combinations of input values (using boolean style AND/OR conditions) and potentially calling multiple subroutines (instead of just a single set of values and 'branch to' program labels). (The switch statement construct in any case may not be available, or has confusingly differing implementations in high level languages (HLL). The control table concept, by comparison, has no intrinsic language dependencies, but might nevertheless be implemented differently according to the available data definition features of the chosen programming language.)
Table content
A control table essentially embodies the 'essence' of a conventional program, stripped of its programming language syntax and platform dependent components (e.g. IF/THEN DO.., FOR.., DO WHILE.., SWITCH, GOTO, CALL) and 'condensed' to its variables (e.g. input1), values (e.g. 'A','S','M' and 'D'), and subroutine identities (e.g. 'Add','subtract,..' or #1, #2,..). The structure of the table itself typically implies the (default) logical operations involved – such as 'testing for equality', performing a subroutine and 'next operation' or following the default sequence (rather than these being explicitly stated within program statements – as required in other programming paradigms).
A multi-dimensional control table will normally, as a minimum, contain value/action pairs and may additionally contain operators and type information such as, the location, size and format of input or output data, whether data conversion (or other run-time processing nuances) is required before or after processing (if not already implicit in the function itself). The table may or may not contain indexes or relative or absolute pointers to generic or customized primitives or subroutines to be executed depending upon other values in the "row".
The table illustrated below applies only to 'input1' since no specific input is specified in the table.
conditions and actions implied by structure
(implied) IF = (implied) perform value action value action
(This side-by-side pairing of value and action has similarities to constructs in Event-driven programming, namely 'event-detection' and 'event-handling' but without (necessarily) the asynchronous nature of the event itself)
The variety of values that can be encoded within a control table is largely dependent upon the computer language used. Assembly language provides the widest scope for data types including (for the actions), the option of directly executable machine code. Typically a control table will contain values for each possible matching class of input together with a corresponding pointer to an action subroutine. Some languages claim not to support pointers (directly) but nevertheless can instead support an index which can be used to represent a 'relative subroutine number' to perform conditional execution, controlled by the value in the table entry (e.g. for use in an optimized SWITCH statement – designed with zero gaps (i.e. a multiway branch) ).
Comments positioned above each column (or even embedded textual documentation) can render a decision table 'human readable' even after 'condensing down' (encoding) to its essentials (and still broadly in-line with the original program specification – especially if a printed decision table, enumerating each unique action, is created before coding begins). The table entries can also optionally contain counters to collect run-time statistics for 'in-flight' or later optimization
Table location
Control tables can reside in static storage, on auxiliary storage, such as a flat file or on a database or may alternatively be partially or entirely built dynamically at program initialization time from parameters (which themselves may reside in a table). For optimum efficiency, the table should be memory resident when the interpreter begins to use it.
The interpreter and subroutines
The interpreter can be written in any suitable programming language including a high level language. A suitably designed generic interpreter, together with a well chosen set of generic subroutines (able to process the most commonly occurring primitives), would require additional conventional coding only for new custom subroutines (in addition to specifying the control table itself). The interpreter, optionally, may only apply to some well-defined sections of a complete application program (such as the main control loop) and not other, 'less conditional', sections (such as program initialization, termination and so on).
The interpreter does not need to be unduly complex, or produced by a programmer with the advanced knowledge of a compiler writer, and can be written just as any other application program – except that it is usually designed with efficiency in mind. Its primary function is to "execute" the table entries as a set of "instructions". There need be no requirement for parsing of control table entries and these should therefore be designed, as far as possible, to be 'execution ready', requiring only the "plugging in" of variables from the appropriate columns to the already compiled generic code of the interpreter. The program instructions are, in theory, infinitely extensible and constitute (possibly arbitrary) values within the table that are meaningful only to the interpreter. The control flow of the interpreter is normally by sequential processing of each table row but may be modified by specific actions in the table entries.
These arbitrary values can thus be designed with efficiency in mind – by selecting values that can be used as direct indexes to data or function pointers. For particular platforms/language, they can be specifically designed to minimize instruction path lengths using branch table values or even, in some cases such as in JIT compilers, consist of directly executable machine code "snippets" (or pointers to them).
The subroutines may be coded either in the same language as the interpreter itself or any other supported program language (provided that suitable inter-language 'Call' linkage mechanisms exist). The choice of language for the interpreter and/or subroutines will usually depend upon how portable it needs to be across various platforms. There may be several versions of the interpreter to enhance the portability of a control table. A subordinate control table pointer may optionally substitute for a subroutine pointer in the 'action' columns if the interpreter supports this construct, representing a conditional 'drop' to a lower logical level, mimicking a conventional structured program structure.
Performance considerations
At first sight, the use of control tables would appear to add quite a lot to a program's overhead, requiring, as it does, an interpreter process before the 'native' programming language statements are executed. This however is not always the case. By separating (or 'encapsulating') the executable coding from the logic, as expressed in the table, it can be more readily targeted to perform its function most efficiently. This may be experienced most obviously in a spreadsheet application – where the underlying spreadsheet software transparently converts complex logical 'formulae' in the most efficient manner it is able, in order to display its results.
The examples below have been chosen partly to illustrate potential performance gains that may not only compensate significantly for the additional tier of abstraction, but also improve upon – what otherwise might have been – less efficient, less maintainable and lengthier code. Although the examples given are for a 'low level' assembly language and for the C language, it can be seen, in both cases, that very few lines of code are required to implement the control table approach and yet can achieve very significant constant time performance improvements, reduce repetitive source coding and aid clarity, as compared with verbose conventional program language constructs. See also the quotations by Donald Knuth, concerning tables and the efficiency of multiway branching in this article.
Examples of control tables
The following examples are arbitrary (and based upon just a single input for simplicity), however the intention is merely to demonstrate how control flow can be effected via the use of tables instead of regular program statements. It should be clear that this technique can easily be extended to deal with multiple inputs, either by increasing the number of columns or utilizing multiple table entries (with optional and/or operator). Similarly, by using (hierarchical) 'linked' control tables, structured programming can be accomplished (optionally using indentation to help highlight subordinate control tables).
"CT1" is an example of a control table that is a simple lookup table. The first column represents the input value to be tested (by an implied 'IF input1 = x') and, if TRUE, the corresponding 2nd column (the 'action') contains a subroutine address to perform by a call (or jump to – similar to a SWITCH statement). It is, in effect, a multiway branch with return (a form of "dynamic dispatch"). The last entry is the default case where no match is found.
CT1
input 1 pointer A -->Add S -->Subtract M -->Multiply D -->Divide ? -->Default
For programming languages that support pointers within data structures alongside other data values, the above table (CT1) can be used to direct control flow to an appropriate subroutines according to matching value from the table (without a column to indicate otherwise, equality is assumed in this simple case).
Assembly language example for IBM/360 (maximum 16Mb address range) or Z/Architecture
No attempt is made to optimize the lookup in coding for this first example, and it uses instead a simple linear search technique – purely to illustrate the concept and demonstrate fewer source lines. To handle all 256 different input values, approximately 265 lines of source code would be required (mainly single line table entries) whereas multiple 'compare and branch' would have normally required around 512 source lines (the size of the binary is also approximately halved, each table entry requiring only 4 bytes instead of approximately 8 bytes for a series of 'compare immediate'/branch instructions (For larger input variables, the saving is even greater).
* ------------------ interpreter --------------------------------------------*
LM R14,R0,=A(4,CT1,N) Set R14=4, R15 --> table, and R0 =no. of entries in table (N)
TRY CLC INPUT1,0(R15) ********* Found value in table entry ?
BE ACTION * loop * YES, Load register pointer to sub-routine from table
AR R15,R14 * * NO, Point to next entry in CT1 by adding R14 (=4)
BCT R0,TRY ********* Back until count exhausted, then drop through
. default action ... none of the values in table match, do something else
LA R15,4(R15) point to default entry (beyond table end)
ACTION L R15,0(R15) get pointer into R15,from where R15 points
BALR R14,R15 Perform the sub-routine ("CALL" and return)
B END go terminate this program
* ------------------ control table -----------------------------------------*
* | this column of allowable EBCDIC or ASCII values is tested '=' against variable 'input1'
* | | this column is the 3-byte address of the appropriate subroutine
* v v
CT1 DC C'A',AL3(ADD) START of Control Table (4 byte entry length)
DC C'S',AL3(SUBTRACT)
DC C'M',AL3(MULTIPLY)
DC C'D',AL3(DIVIDE)
N EQU (*-CT1)/4 number of valid entries in table (total length / entry length)
DC C'?',AL3(DEFAULT) default entry – used on drop through to catch all
INPUT1 DS C input variable is in this variable
* ------------------ sub-routines ------------------------------------------*
ADD CSECT sub-routine #1 (shown as separate CSECT here but might
. alternatively be in-line code)
. instruction(s) to add
BR R14 return
SUBTRACT CSECT sub-routine #2
. instruction(s) to subtract
BR R14 return
. etc..
improving the performance of the interpreter in above example
- To make a selection in the example above, the average instruction path length (excluding the subroutine code) is '4n/2 +3', but can easily be reduced, where n = 1 to 64, to a constant time with a path length of '5' with zero comparisons, if a 256 byte translate table is first utilized to create a direct index to CT1 from the raw EBCDIC data. Where n = 6, this would then be equivalent to just 3 sequential compare & branch instructions. However, where n<=64, on average it would need approximately 13 times less instructions than using multiple compares. Where n=1 to 256, on average it would use approximately 42 times less instructions - since, in this case, one additional instruction would be required (to multiply the index by 4).
Improved interpreter (up to 26 times less executed instructions than the above example on average, where n= 1 to 64 and up to 13 times less than would be needed using multiple comparisons).
To handle 64 different input values, approximately 85 lines of source code (or less) are required (mainly single line table entries) whereas multiple 'compare and branch' would require around 128 lines (the size of the binary is also almost halved – despite the additional 256 byte table required to extract the 2nd index).
* ------------------ interpreter --------------------------------------------*
SR R14,R14 ********* Set R14=0
CALC IC R14,INPUT1 * calc * put EBCDIC byte into lo order bits (24–31) of R14
IC R14,CT1X(R14) * * use EBCDIC value as index on table 'CT1X' to get new index
FOUND L R15,CT1(R14) ********* get pointer to subroutine using index (0,4, 8 etc.)
BALR R14,R15 Perform the sub-routine ("CALL" and return or Default)
B END go terminate this program
* --------------- additional translate table (EBCDIC --> pointer table INDEX) 256 bytes----*
CT1X DC 12AL1(00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00) 12 identical sets of 16 bytes of x'00
* representing X'00 – x'BF'
DC AL1(00,04,00,00,16,00,00,00,00,00,00,00,00,00,00,00) ..x'C0' – X'CF'
DC AL1(00,00,00,00,12,00,00,00,00,00,00,00,00,00,00,00) ..x'D0' – X'DF'
DC AL1(00,00,08,00,00,00,00,00,00,00,00,00,00,00,00,00) ..x'E0' – X'EF'
DC AL1(00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00) ..x'F0' – X'FF'
* the assembler can be used to automatically calculate the index values and make the values more user friendly
* (for e.g. '04' could be replaced with the symbolic expression 'PADD-CT1' in table CT1X above)
* modified CT1 (added a default action when index = 00, single dimension, full 31 bit address)
CT1 DC A(DEFAULT) index =00 START of Control Table (4 byte address constants)
PADD DC A(ADD) =04
PSUB DC A(SUBTRACT) =08
PMUL DC A(MULTIPLY) =12
PDIV DC A(DIVIDE) =16
* the rest of the code remains the same as first example
Further improved interpreter (up to 21 times less executed instructions (where n>=64) than the first example on average and up to 42 times less than would be needed using multiple comparisons).
To handle 256 different input values, approximately 280 lines of source code or less, would be required (mainly single line table entries), whereas multiple 'compare and branch' would require around 512 lines (the size of the binary is also almost halved once more).
* ------------------ interpreter --------------------------------------------*
SR R14,R14 ********* Set R14=0
CALC IC R14,INPUT1 * calc * put EBCDIC byte into lo order bits (24–31) of R14
IC R14,CT1X(R14) * * use EBCDIC value as index on table 'CT1X' to get new index
SLL R14,2 * * multiply index by 4 (additional instruction)
FOUND L R15,CT1(R14) ********* get pointer to subroutine using index (0,4, 8 etc.)
BALR R14,R15 Perform the sub-routine ("CALL" and return or Default)
B END go terminate this program
* --------------- additional translate table (EBCDIC --> pointer table INDEX) 256 bytes----*
CT1X DC 12AL1(00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00) 12 identical sets of 16 bytes of x'00'
* representing X'00 – x'BF'
DC AL1(00,01,00,00,04,00,00,00,00,00,00,00,00,00,00,00) ..x'C0' – X'CF'
DC AL1(00,00,00,00,03,00,00,00,00,00,00,00,00,00,00,00) ..x'D0' – X'DF'
DC AL1(00,00,02,00,00,00,00,00,00,00,00,00,00,00,00,00) ..x'E0' – X'EF'
DC AL1(00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00) ..x'F0' – X'FF'
* the assembler can be used to automatically calculate the index values and make the values more user friendly
* (for e.g. '01' could be replaced with the symbolic expression 'PADD-CT1/4' in table CT1X above)
* modified CT1 (index now based on 0,1,2,3,4 not 0,4,8,12,16 to allow all 256 variations)
CT1 DC A(DEFAULT) index =00 START of Control Table (4 byte address constants)
PADD DC A(ADD) =01
PSUB DC A(SUBTRACT) =02
PMUL DC A(MULTIPLY) =03
PDIV DC A(DIVIDE) =04
* the rest of the code remains the same as the 2nd example
C language example This example in C uses two tables, the first (CT1) is a simple linear search one-dimensional lookup table – to obtain an index by matching the input (x), and the second, associated table (CT1p), is a table of addresses of labels to jump to.
static const char CT1[] = { "A", "S", "M", "D" }; /* permitted input values */
static const void *CT1p[] = { &&Add, &&Subtract, &&Multiply, &&Divide, &&Default}; /* labels to goto & default*/
for (int i = 0; i < sizeof(CT1); i++) /* loop thru ASCII values */
{if (x==CT1[i]) goto *CT1p[i]; } /* found --> appropriate label */
goto *CT1p[i+1]; /* not found --> default label */
This can be made more efficient if a 256 byte table is used to translate the raw ASCII value (x) directly to a dense sequential index value for use in directly locating the branch address from CT1p (i.e. "index mapping" with a byte-wide array). It will then execute in constant time for all possible values of x (If CT1p contained the names of functions instead of labels, the jump could be replaced with a dynamic function call, eliminating the switch-like goto – but decreasing performance by the additional cost of function housekeeping).
static const void *CT1p[] = {&&Default, &&Add, &&Subtract, &&Multiply, &&Divide};
/* the 256 byte table, below, holds values (1,2,3,4), in corresponding ASCII positions (A,S,M,D), all others set to 0x00 */
static const char CT1x[]={
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x01', '\x00', '\x00', '\x04', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x03', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x02', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x03', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00',
'\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00', '\x00'};
/* the following code will execute in constant time, irrespective of the value of the input character (x) */
i = CT1x(x); /* extract the correct subroutine index from table CT1x using its ASCII value as an index initially */
goto *CT1p[i]; /* goto (Switch to) the label corresponding to the index (0=default,1= Add,2= Subtract,.) - see CT1p */
The next example below illustrates how a similar effect can be achieved in languages that do not support pointer definitions in data structures but do support indexed branching to a subroutine – contained within a (0-based) array of subroutine pointers. The table (CT2) is used to extract the index (from 2nd column) to the pointer array (CT2P). If pointer arrays are not supported, a SWITCH statement or equivalent can be used to alter the control flow to one of a sequence of program labels (e.g.: case0,case1,case2,case3,case4) which then either process the input directly, or else perform a call (with return) to the appropriate subroutine (default,Add,Subtract,Multiply or Divide,..) to deal with it.
CT2
input 1 subr # A 1 S 2 M 3 D 4 ? 0
As in above examples, it is possible to very efficiently translate the potential ASCII input values (A,S,M,D or unknown) into a pointer array index without actually using a table lookup, but is shown here as a table for consistency with the first example.
Multi-dimensional control tables can be constructed (i.e. customized) that can be 'more complex' than the above examples that might test for multiple conditions on multiple inputs or perform more than one 'action', based on some matching criteria. An 'action' can include a pointer to another subordinate control table. The simple example below has had an implicit 'OR' condition incorporated as an extra column (to handle lower case input, however in this instance, this could equally have been handled simply by having an extra entry for each of the lower case characters specifying the same subroutine identifier as the upper case characters). An extra column to count the actual run-time events for each input as they occur is also included.
CT3
input 1 alternate subr # count A a 1 0 S s 2 0 M m 3 0 D d 4 0 ? ? 0 0
The control table entries are then much more similar to conditional statements in procedural languages but, crucially, without the actual (language dependent) conditional statements (i.e. instructions) being present (the generic code is physically in the interpreter that processes the table entries, not in the table itself – which simply embodies the program logic via its structure and values).
In tables such as these, where a series of similar table entries defines the entire logic, a table entry number or pointer may effectively take the place of a program counter in more conventional programs and may be reset in an 'action', also specified in the table entry. The example below (CT4) shows how extending the earlier table, to include a 'next' entry (and/or including an 'alter flow' (jump) subroutine) can create a loop (This example is actually not the most efficient way to construct such a control table but, by demonstrating a gradual 'evolution' from the first examples above, shows how additional columns can be used to modify behaviour.) The fifth column demonstrates that more than one action can be initiated with a single table entry – in this case an action to be performed after the normal processing of each entry ('-' values mean 'no conditions' or 'no action').
Structured programming or "Goto-less" code, (incorporating the equivalent of 'DO WHILE' or 'for loop' constructs), can also be accommodated with suitably designed and 'indented' control table structures.
CT4 (a complete 'program' to read input1 and process, repeating until 'E' encountered)
input 1 alternate subr # count jump - - 5 0 - E e 7 0 - A a 1 0 - S s 2 0 - M m 3 0 - D d 4 0 - ? ? 0 0 - - - 6 0 1
Table-driven rating
In the specialist field of telecommunications rating (concerned with the determining the cost of a particular call), table-driven rating techniques illustrate the use of control tables in applications where the rules may change frequently because of market forces. The tables that determine the charges may be changed at short notice by non-programmers in many cases.[4][5]
If the algorithms are not pre-built into the interpreter (and therefore require additional runtime interpretation of an expression held in the table), it is known as "Rule-based Rating" rather than table-driven rating (and consequently consumes significantly more overhead).
Spreadsheets
A spreadsheet data sheet can be thought of as a two dimensional control table, with the non empty cells representing data to the underlying spreadsheet program (the interpreter). The cells containing formula are usually prefixed with an equals sign and simply designate a special type of data input that dictates the processing of other referenced cells – by altering the control flow within the interpreter. It is the externalization of formulae from the underlying interpreter that clearly identifies both spreadsheets, and the above cited "rule based rating" example as readily identifiable instances of the use of control tables by non programmers.
Programming paradigm
If the control tables technique could be said to belong to any particular programming paradigm, the closest analogy might be Automata-based programming or "reflective" (a form of metaprogramming – since the table entries could be said to 'modify' the behaviour of the interpreter). The interpreter itself however, and the subroutines, can be programmed using any one of the available paradigms or even a mixture. The table itself can be essentially a collection of "raw data" values that do not even need to be compiled and could be read in from an external source (except in specific, platform dependent, implementations using memory pointers directly for greater efficiency).
Analogy to bytecode / virtual machine instruction set
A multi-dimensional control table has some conceptual similarities to bytecode operating on a virtual machine, in that a platform dependent "interpreter" program is usually required to perform the actual execution (that is largely conditionally determined by the tables content). There are also some conceptual similarities to the recent Common Intermediate Language (CIL) in the aim of creating a common intermediate 'instruction set' that is independent of platform (but unlike CIL, no pretensions to be used as a common resource for other languages). P-code can also be considered a similar but earlier implementation with origins as far back as 1966.
Instruction fetch
When a multi-dimensional control table is used to determine program flow, the normal "hardware" Program Counter function is effectively simulated with either a pointer to the first (or next) table entry or else an index to it. "Fetching" the instruction involves decoding the data in that table entry – without necessarily copying all or some of the data within the entry first. Programming languages that are able to use pointers have the dual advantage that less overhead is involved, both in accessing the contents and also advancing the counter to point to the next table entry after execution. Calculating the next 'instruction' address (i.e. table entry) can even be performed as an optional additional action of every individual table entry allowing loops and or jump instructions at any stage.
Monitoring control table execution
The interpreter program can optionally save the program counter (and other relevant details depending upon instruction type) at each stage to record a full or partial trace of the actual program flow for debugging purposes, hot spot detection, code coverage analysis and performance analysis (see examples CT3 & CT4 above).
Advantages
- clarity – Information tables are ubiquitous and mostly inherently understood even by the general public (especially fault diagnostic tables in product guides)
- portability – can be designed to be 100% language independent (and platform independent – except for the interpreter)
- flexibility – ability to execute either primitives or subroutines transparently and be custom designed to suit the problem
- compactness – table usually shows condition/action pairing side-by-side (without the usual platform/language implementation dependencies), often also resulting in
- binary file – reduced in size through less duplication of instructions
- source file – reduced in size through elimination of multiple conditional statements
- improved program load (or download) speeds
- maintainability – tables often reduce the number of source lines needed to be maintained v. multiple compares
- locality of reference – compact tables structures result in tables remaining in cache
- code re-use – the "interpreter" is usually reusable. Frequently it can be easily adapted to new programming tasks using precisely the same technique and can grow 'organically' becoming, in effect, a standard library of tried and tested subroutines, controlled by the table definitions.
- efficiency – systemwide optimization possible. Any performance improvement to the interpreter usually improves all applications using it (see examples in 'CT1' above).
- extensible – new 'instructions' can be added – simply by extending the interpreter
- interpreter can be written like an application program
Optionally:-
- the interpreter can be introspective and "self optimize" using runtime metrics collected within the table itself (see CT3 and CT4 – with entries that could be periodically sorted by descending count). The interpreter can also optionally choose the most efficient lookup technique dynamically from metrics gathered at run-time (e.g. size of array, range of values, sorted or unsorted)
- dynamic dispatch – common functions can be pre-loaded and less common functions fetched only on first encounter to reduce memory usage. In-table memoization can be employed to achieve this.
- The interpreter can have debugging, trace and monitor features built-in – that can then be switched on or off at will according to test or 'live' mode
- control tables can be built 'on-the-fly' (according to some user input or from parameters) and then executed by the interpreter (without building code literally).
Disadvantages
- training requirement – application programmers are not usually trained to produce generic solutions
The following mainly apply to their use in multi-dimensional tables, not the one-dimensional tables discussed earlier.
- overhead – some increase because of extra level of indirection caused by virtual instructions having to be 'interpreted' (this however can usually be more than offset by a well designed generic interpreter taking full advantage of efficient direct translate, search and conditional testing techniques that may not otherwise have been utilized)
- Complex expressions cannot always be used directly in data table entries for comparison purposes
- (these 'intermediate values' can however be calculated beforehand instead within a subroutine and their values referred to in the conditional table entries. Alternatively, a subroutine can perform the complete complex conditional test (as an unconditional 'action') and, by setting a truth flag as its result, it can then be tested in the next table entry. See Structured program theorem)
Quotations
Multiway branching is an important programming technique which is all too often replaced by an inefficient sequence of if tests. Peter Naur recently wrote me that he considers the use of tables to control program flow as a basic idea of computer science that has been nearly forgotten; but he expects it will be ripe for rediscovery any day now. It is the key to efficiency in all the best compilers I have studied.
— Donald Knuth, Structured Programming with go to Statements
There is another way to look at a program written in interpretative language. It may be regarded as a series of subroutine calls, one after another. Such a program may in fact be expanded into a long sequence of calls on subroutines, and, conversely, such a sequence can usually be packed into a coded form that is readily interpreted. The advantage of interpretive techniques are the compactness of representation, the machine independence, and the increased diagnostic capability. An interpreter can often be written so that the amount of time spent in interpretation of the code itself and branching to the appropriate routine is negligible
— Donald Knuth, The Art of Computer Programming Volume 1, 1997, page 202
The space required to represent a program can often be decreased by the use of interpreters in which common sequences of operations are represented compactly. A typical example is the use of a finite-state machine to encode a complex protocol or lexical format into a small table
— Jon Bentley, Writing Efficient Programs
Jump tables can be especially efficient if the range tests can be omitted. For example, if the control value is an enumerated type (or a character) then it can only contain a small fixed range of values and a range test is redundant provided the jump table is large enough to handle all possible values
— David.A. SPULER, Compiler Code Generation for Multiway Branch Statements as a Static Search Problem
Programs must be written for people to read, and only incidentally for machines to execute.
— "Structure and Interpretation of Computer Programs", preface to the first edition, Abelson & Sussman
Show me your flowchart and conceal your tables, and I shall continue to be mystified. Show me your tables, and I won't usually need your flowchart; it'll be obvious.
— "The Mythical Man-Month: Essays on Software Engineering", Fred Brooks
See also
- Automata-based programming
- Database-centric architecture
- Data-driven testing
- Decision table
- Finite-state machine
- Keyword-driven testing
- Pointer (computer programming)
- Switch statement – multiway branching to one of a number of program labels, depending upon a single input variable
- Threaded code
- Token threading
Notes
- Programs from decision tables, Humby, E., 2007,Macdonald, 1973 ... Biggerstaff, Ted J. Englewood Cliffs, NJ : Prentice-Hall ISBN 0-444-19569-6
- UML state machine#Hierarchically nested states
- Carl Wright, Service Level Corpo. (2002) Program Code Based vs. Table-driven vs. Rule-Based Rating, Rating Matters issue n. 12, 13 November 2002 ISSN 1532-1886
- Brian E. Clauser, Melissa J. Margolis, Stephen G. Clyman, Linette P. Ross (1997) Development of Automated Scoring Algorithms for Complex Performance Assessments: A Comparison of Two Approaches Journal of Educational Measurement, Vol. 34, No. 2 (Summer, 1997), pp. 141–161
References
External links
- Switch statement in Windows PowerShell describes extensions to standard switch statement (providing some similar features to control tables)
- Control Table example in "C" language using pointers, by Christopher Sawtell c1993, Department of Computer Science, University of Auckland
- Table driven design by Wayne Cunneyworth of DataKinetics
- From Requirements to Tables to Code and Tests By George Brooke
- Some comments on the use of ambiguous decision tables and their conversion to computer programs by P. J. H. King and R. G. Johnson, Univ. of London, London, UK
- Ambiguity in limited entry decision tables by P. J. H. King
- Conversion of decision tables to computer programs by rule mask techniques by P. J. H. King
- A Superoptimizer Analysis of Multiway Branch Code Generation section 3.9, page 16 index mapping
- Jump Tables via Function Pointer Arrays in C/C++ Jones, Nigel. "Arrays of Pointers to Functions " Embedded Systems Programming, May 1999.
- Page view statistics for this article for December 2009
