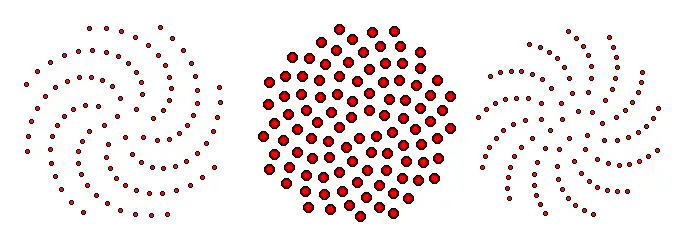
Fermat's spiral
A Fermat's spiral or parabolic spiral is a plane curve named after Pierre de Fermat.[1] Its polar coordinate representation is given by


which describes a parabola with horizontal axis.
Fermat's spiral is similar to the Archimedean spiral. But an Archimedean spiral has always the same distance between neighboring arcs, which is not true for Fermat's spiral.
Like other spirals Fermat's spiral is used for curvature continuous blending of curves.[1]
In Cartesian coordinates
Fermat's spiral with polar equation
can be described in Cartesian coordinates (x = r cos φ, y = r sin φ) by the parametric representation
From the parametric representation and φ = r2/a2, r = √x2 + y2 one gets a representation by an equation:
Geometric properties
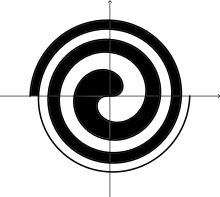
Division of the plane
A complete Fermat's spiral (both branches) is a smooth double point free curve, in contrast with the Archimedean and hyperbolic spiral. It divides the plane (like a line or circle or parabola) into two connected regions. But this division is less obvious than the division by a line or circle or parabola. It is not obvious to which side a chosen point belongs.

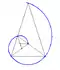
Polar slope
From vector calculus in polar coordinates one gets the formula
for the polar slope and its angle α between the tangent of a curve and the corresponding polar circle (see diagram).
For Fermat's spiral r = a√φ one gets
Hence the slope angle is monotonely decreasing.
Curvature
From the formula
for the curvature of a curve with polar equation r = r(φ) and its derivatives
one gets the curvature of a Fermat's spiral:
At the origin the curvature is 0. Hence the complete curve has at the origin an inflection point and the x-axis is its tangent there.
Area between arcs
The area of a sector of Fermat's spiral between two points (r(φ1), φ1) and (r(φ1), φ1) is
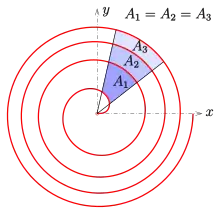
After raising both angles by 2π one gets
Hence the area A of the region between two neighboring arcs is
A only depends on the difference of the two angles, not on the angles themselves.
For the example shown in the diagram, all neighboring stripes have the same area: A1 = A2 = A3.
This property is used in electrical engineering for the construction of variable capacitors. [2]

Special case due to Fermat
In 1636, Fermat wrote a letter [3] to Marin Mersenne which contains the following special case:
Let φ1 = 0, φ2 = 2π; then the area of the black region (see diagram) is A0 = a2π2, which is half of the area of the circle K0 with radius r(2π). The regions between neighboring curves (white, blue, yellow) have the same area A = 2a2π2. Hence:
- The area between two arcs of the spiral after a full turn equals the area of the circle K0.
Arclength
The length of the arc of Fermat's spiral between two points (r(φ1), φ1) can be calculated by the integral:
This integral leads to an elliptical integral, which can be solved numerically.
Circle inversion
The inversion at the unit circle has in polar coordinates the simple description (r, φ) ↦ (1/r, φ).
- The image of Fermat's spiral r = a√φ under the inversion at the unit circle is a lituus spiral with polar equation
- When φ = 1/a2, both curves intersect at a fixed point on the unit circle.
- The tangent (x-axis) at the inflection point (origin) of Fermat's spiral is mapped onto itself and is the asymptotic line of the lituus spiral.
The golden ratio and the golden angle
In disc phyllotaxis, as in the sunflower and daisy, the mesh of spirals occurs in Fibonacci numbers because divergence (angle of succession in a single spiral arrangement) approaches the golden ratio. The shape of the spirals depends on the growth of the elements generated sequentially. In mature-disc phyllotaxis, when all the elements are the same size, the shape of the spirals is that of Fermat spirals—ideally. That is because Fermat's spiral traverses equal annuli in equal turns. The full model proposed by H. Vogel in 1979[4] is
where θ is the angle, r is the radius or distance from the center, and n is the index number of the floret and c is a constant scaling factor. The angle 137.508° is the golden angle which is approximated by ratios of Fibonacci numbers.[5]
The resulting spiral pattern of unit disks should be distinguished from the Doyle spirals, patterns formed by tangent disks of geometrically increasing radii placed on logarithmic spirals.
Solar plants
Fermat's spiral has also been found to be an efficient layout for the mirrors of concentrated solar power plants.[6]
References
- Anastasios M. Lekkas, Andreas R. Dahl, Morten Breivik, Thor I. Fossen: "Continuous-Curvature Path Generation Using Fermat's Spiral". In: Modeling, Identification and Control. Vol. 34, No. 4, 2013, pp. 183–198, ISSN 1890-1328.
- Fritz Wicke: Einführung in die höhere Mathematik. Springer-Verlag, 2013, ISBN 978-3-662-36804-6, p. 414.
- Lettre de Fermat à Mersenne du 3 juin 1636, dans Paul Tannery. In: Oeuvres de Fermat. T. III, S. 277, Lire en ligne.
- Vogel, H (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (44): 179–189. doi:10.1016/0025-5564(79)90080-4.
- Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.
- Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. doi:10.1016/j.solener.2011.12.007.
Further reading
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 31, 186. ISBN 0-486-60288-5.
External links
- Fermat’s spiral at the Encyclopædia Britannica
- "Fermat spiral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Online exploration using JSXGraph (JavaScript)
- Fermat's Natural Spirals, in sciencenews.org