Freundlich equation

The Freundlich equation or Freundlich adsorption isotherm, an adsorption isotherm, is an empirical relationship between the quantity of a gas adsorbed into a solid surface and the gas pressure. The same relationship is also applicable for the concentration of a solute adsorbed onto the surface of a solid and the concentration of the solute in the liquid phase. In 1909, Herbert Freundlich gave an expression representing the isothermal variation of adsorption of a quantity of gas adsorbed by unit mass of solid adsorbent with gas pressure.[1] This equation is known as Freundlich adsorption isotherm or Freundlich adsorption equation. As this relationship is entirely empirical, in the case where adsorption behavior can be properly fit by isotherms with a theoretical basis, it is usually appropriate to use such isotherms instead (see for example the Langmuir and BET adsorption theories). The Freundlich equation is also derived (non-empirically) by attributing the change in the equilibrium constant of the binding process to the heterogeneity of the surface and the variation in the heat of adsorption.[2]

Freundlich adsorption isotherm
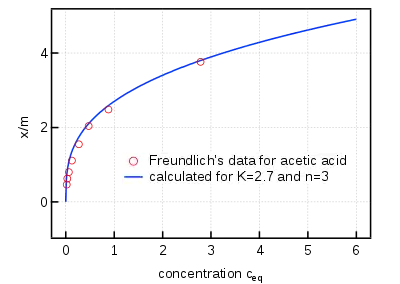
Freundlich's original data for adsorption of acetic acid (page 392 in [3]) and a fit according to Freundlich's exponential law.

The Freundlich adsorption isotherm is mathematically expressed as

It is also written as

or

It is also written as

where

x = mass of adsorbate
m = mass of adsorbent
p = equilibrium pressure of the gaseous adsorbate in case of experiments made in the gas phase (gas/solid interaction with gaseous species/adsorbed species)
c = equilibrium concentration of adsorbate in case of experiments made with an aqueous solution in contact with a dispersed solid phase (dissolved species/adsorbed species).

K and n are constants for a given adsorbate and adsorbent at a given temperature (from there, the term isotherm needed to avoid significant gas pressure fluctuations due to uncontrolled temperature variations in the case of adsorption experiments of a gas onto a solid phase).

At high pressure 1/n = 0, hence extent of adsorption becomes independent of pressure.

The Freundlich equation is unique; consequently, if the data fit the equation, it is only likely, but not proved, that the surface is heterogeneous. The heterogeneity of the surface can be confirmed with calorimetry. Homogeneous surfaces (or heterogeneous surfaces that exhibit homogeneous adsorption (single site)) have a constant ΔH of adsorption.[4] On the other hand, heterogeneous adsorption (multi-site) have a variable ΔH of adsorption depending on the percent of sites occupied. When the adsorbate pressure in the gas phase (or the concentration in solution) is low, high-energy sites will be occupied first. As the pressure in the gas phase (or the concentration in solution) increases, the low-energy sites will then be occupied resulting in a weaker ΔH of adsorption.[5]

Limitation of Freundlich adsorption isotherm

Experimentally it was determined that extent of gas adsorption varies directly with pressure, and then it directly varies with pressure raised to the power 1/n until saturation pressure Ps is reached. Beyond that point, the rate of adsorption saturates even after applying higher pressure. Thus, the Freundlich adsorption isotherm fails at higher pressure.

See also

References
  1. Freundlich, Herbert. Kapillarchemie, eine Darstellung der Chemie der Kolloide und verwandter Gebiete. Akademische Verlagsgesellschaft, 1909.
  2. Adamson, A.W (1997). Physical chemistry of surfaces. p. 393.
  3. Freundlich, Herbert (1907). " Über die Adsorption in Lösungen." Zeitschrift für Physikalische Chemie – Stöchiometrie und Verwandschaftslehre. 57 (4), 385–470.
  4. Burke GM, Wurster DE, Buraphacheep V, Berg MJ, Veng-Pedersen P, Schottelius DD. Model selection for the adsorption of phenobarbital by activated charcoal. Pharm Res. 1991 Feb;8(2):228-31. doi: 10.1023/a:1015800322286. PMID: 2023872.
  5. Adamson, A.W (1997). Physical chemistry of surfaces. p. 699.

Further reading
  • Jaroniec, M. (1975). "Adsorption on heterogeneous surfaces: The exponential equation for the overall adsorption isotherm". Surface Science. 50 (2): 553–564. Bibcode:1975SurSc..50..553J. doi:10.1016/0039-6028(75)90044-8.
  • Levan, M. Douglas; Vermeulen, Theodore (1981). "LeVan, M. Douglas, and Theodore Vermeulen. "Binary Langmuir and Freundlich isotherms for ideal adsorbed solutions." The Journal of Physical Chemistry 85.22 (1981): 3247-3250". The Journal of Physical Chemistry. 85 (22): 3247–3250. doi:10.1021/j150622a009.
  • "Freundlich Equation". Archived from the original on 3 March 2016.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.