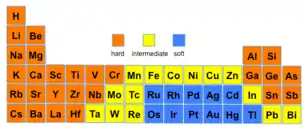
HSAB theory

HSAB concept is an initialism for "hard and soft (Lewis) acids and bases". Also known as the Pearson acid-base concept, HSAB is widely used in chemistry for explaining stability of compounds, reaction mechanisms and pathways. It assigns the terms 'hard' or 'soft', and 'acid' or 'base' to chemical species. 'Hard' applies to species which are small, have high charge states (the charge criterion applies mainly to acids, to a lesser extent to bases), and are weakly polarizable. 'Soft' applies to species which are big, have low charge states and are strongly polarizable.[1]

The theory is used in contexts where a qualitative, rather than quantitative, description would help in understanding the predominant factors which drive chemical properties and reactions. This is especially so in transition metal chemistry, where numerous experiments have been done to determine the relative ordering of ligands and transition metal ions in terms of their hardness and softness.

HSAB theory is also useful in predicting the products of metathesis reactions. In 2005 it was shown that even the sensitivity and performance of explosive materials can be explained on basis of HSAB theory.[2]

Ralph Pearson introduced the HSAB principle in the early 1960s[3][4][5] as an attempt to unify inorganic and organic reaction chemistry.[6]

Theory

Hard-soft trends for acids and bases

Acids

Bases

Essentially, the theory states that soft acids react faster and form stronger bonds with soft bases, whereas hard acids react faster and form stronger bonds with hard bases, all other factors being equal.[7] The classification in the original work was mostly based on equilibrium constants for reaction of two Lewis bases competing for a Lewis acid.

Comparing tendencies of hard acids and bases vs. soft acids and bases
Property	Hard acids and bases	Soft acids and bases
atomic/ionic radius	small	large
oxidation state	high	low or zero
polarizability	low	high
electronegativity (bases)	high	low
HOMO energy of bases[7][8]	low	higher
LUMO energy of acids[7][8]	high	lower (but > soft-base HOMO)
affinity	ionic bonding	covalent bonding

Examples of hard and soft acids and bases
Acids				Bases
hard		soft		hard		soft
Hydronium	H₃O⁺	Mercury	CH₃Hg⁺, Hg²⁺, Hg₂²⁺	Hydroxide	OH⁻	Hydride	H⁻
Alkali metals	Li⁺,Na⁺,K⁺	Platinum	Pt²⁺	Alkoxide	RO⁻	Thiolate	RS⁻
Titanium	Ti⁴⁺	Palladium	Pd²⁺	Halogens	F⁻,Cl⁻	Halogens	I⁻
Chromium	Cr³⁺,Cr⁶⁺	Silver	Ag⁺	Ammonia	NH₃	Phosphine	PR₃
Boron trifluoride	BF₃	Borane	BH₃	Carboxylate	CH₃COO⁻	Thiocyanate	SCN⁻
Carbocation	R₃C⁺	P-chloranil		Carbonate	CO₃²⁻	Carbon monoxide	CO
Lanthanides	Ln³⁺	Bulk metals	M⁰	Hydrazine	N₂H₄	Benzene	C₆H₆
Thorium, uranium	Th⁴⁺, U⁴⁺	Gold	Au⁺

Borderline cases are also identified: borderline acids are trimethylborane, sulfur dioxide and ferrous Fe²⁺, cobalt Co²⁺ caesium Cs⁺ and lead Pb²⁺ cations. Borderline bases are: aniline, pyridine, nitrogen N₂ and the azide, chloride, bromide, nitrate and sulfate anions.

Generally speaking, acids and bases interact and the most stable interactions are hard-hard (ionogenic character) and soft-soft (covalent character).

An attempt to quantify the 'softness' of a base consists in determining the equilibrium constant for the following equilibrium:

BH + CH₃Hg⁺ ⇌ H⁺ + CH₃HgB

Where CH₃Hg⁺ (methylmercury ion) is a very soft acid and H⁺ (proton) is a hard acid, which compete for B (the base to be classified).

Some examples illustrating the effectiveness of the theory:

Bulk metals are soft acids and are poisoned by soft bases such as phosphines and sulfides.
Hard solvents such as hydrogen fluoride, water and the protic solvents tend to solvate strong solute bases such as the fluorine anion and the oxygen anions. On the other hand, dipolar aprotic solvents such as dimethyl sulfoxide and acetone are soft solvents with a preference for solvating large anions and soft bases.
In coordination chemistry soft-soft and hard-hard interactions exist between ligands and metal centers.

Chemical hardness

Chemical hardness in electron volt
Acids			Bases
Hydrogen	H⁺	∞	Fluoride	F⁻	7
Aluminium	Al³⁺	45.8	Ammonia	NH₃	6.8
Lithium	Li⁺	35.1	hydride	H⁻	6.8
Scandium	Sc³⁺	24.6	carbon monoxide	CO	6.0
Sodium	Na⁺	21.1	hydroxyl	OH⁻	5.6
Lanthanum	La³⁺	15.4	cyanide	CN⁻	5.3
Zinc	Zn²⁺	10.8	phosphine	PH₃	5.0
Carbon dioxide	CO₂	10.8	nitrite	NO₂⁻	4.5
Sulfur dioxide	SO₂	5.6	Hydrosulfide	SH⁻	4.1
Iodine	I₂	3.4	Methane	CH₃⁻	4.0
Table 2. Chemical hardness data[9]

In 1983 Pearson together with Robert Parr extended the qualitative HSAB theory with a quantitative definition of the chemical hardness (η) as being proportional to the second derivative of the total energy of a chemical system with respect to changes in the number of electrons at a fixed nuclear environment:[9]

\eta ={\frac {1}{2}}\left({\frac {\partial ^{2}E}{\partial N^{2}}}\right)_{Z}

.

The factor of one-half is arbitrary and often dropped as Pearson has noted.[10]

An operational definition for the chemical hardness is obtained by applying a three-point finite difference approximation to the second derivative:[11]

{\begin{aligned}\eta &\approx {\frac {E(N+1)-2E(N)+E(N-1)}{2}}\\&={\frac {(E(N-1)-E(N))-(E(N)-E(N+1))}{2}}\\&={\frac {1}{2}}(I-A)\end{aligned}}

where I is the ionization potential and A the electron affinity. This expression implies that the chemical hardness is proportional to the band gap of a chemical system, when a gap exists.

The first derivative of the energy with respect to the number of electrons is equal to the chemical potential, μ, of the system,

\mu =\left({\frac {\partial E}{\partial N}}\right)_{Z}

,

from which an operational definition for the chemical potential is obtained from a finite difference approximation to the first order derivative as

{\begin{aligned}\mu &\approx {\frac {E(N+1)-E(N-1)}{2}}\\&={\frac {-(E(N-1)-E(N))-(E(N)-E(N+1))}{2}}\\&=-{\frac {1}{2}}(I+A)\end{aligned}}

which is equal to the negative of the electronegativity (χ) definition on the Mulliken scale: μ = −χ.

The hardness and Mulliken electronegativity are related as

2\eta =\left({\frac {\partial \mu }{\partial N}}\right)_{Z}\approx -\left({\frac {\partial \chi }{\partial N}}\right)_{Z}

,

and in this sense hardness is a measure for resistance to deformation or change. Likewise a value of zero denotes maximum softness, where softness is defined as the reciprocal of hardness.

In a compilation of hardness values only that of the hydride anion deviates. Another discrepancy noted in the original 1983 article are the apparent higher hardness of Tl³⁺ compared to Tl⁺.

Modifications

If the interaction between acid and base in solution results in an equilibrium mixture the strength of the interaction can be quantified in terms of an equilibrium constant. An alternative quantitative measure is the heat (enthalpy) of formation of the Lewis acid-base adduct in a non-coordinating solvent. The ECW model is quantitative model that describes and predicts the strength of Lewis acid base interactions, -ΔH . The model assigned E and C parameters to many Lewis acids and bases. Each acid is characterized by an E_A and a C_A. Each base is likewise characterized by its own E_B and C_B. The E and C parameters refer, respectively, to the electrostatic and covalent contributions to the strength of the bonds that the acid and base will form. The equation is

-ΔH = E_AE_B + C_AC_B + W

The W term represents a constant energy contribution for acid–base reaction such as the cleavage of a dimeric acid or base. The equation predicts reversal of acids and base strengths. The graphical presentations of the equation show that there is no single order of Lewis base strengths or Lewis acid strengths.[12] The ECW model accommodates the failure of single parameter descriptions of acid-base interactions.

A related method adopting the E and C formalism of Drago and co-workers quantitatively predicts the formation constants for complexes of many metal ions plus the proton with a wide range of unidentate Lewis acids in aqueous solution, and also offered insights into factors governing HSAB behavior in solution.[13]

Another quantitative system has been proposed, in which Lewis acid strength toward Lewis base fluoride is based on gas-phase affinity for fluoride.[14] Additional one-parameter base strength scales have been presented.[15] However, it has been shown that to define the order of Lewis base strength (or Lewis acid strength) at least two properties must be considered. [16] For Pearson's qualitative HSAB theory the two properties are hardness and strength while for Drago’s quantitative ECW model the two properties are electrostatic and covalent .

Kornblum's rule

An application of HSAB theory is the so-called Kornblum's rule (after Nathan Kornblum) which states that in reactions with ambident nucleophiles (nucleophiles that can attack from two or more places), the more electronegative atom reacts when the reaction mechanism is S_N1 and the less electronegative one in a S_N2 reaction. This rule (established in 1954)[17] predates HSAB theory but in HSAB terms its explanation is that in a S_N1 reaction the carbocation (a hard acid) reacts with a hard base (high electronegativity) and that in a S_N2 reaction tetravalent carbon (a soft acid) reacts with soft bases.

According to findings, electrophilic alkylations at free CN⁻ occur preferentially at carbon, regardless of whether the S_N1 or S_N2 mechanism is involved and whether hard or soft electrophiles are employed. Preferred N attack, as postulated for hard electrophiles by the HSAB principle, could not be observed with any alkylating agent. Isocyano compounds are only formed with highly reactive electrophiles that react without an activation barrier because the diffusion limit is approached. It is claimed that the knowledge of absolute rate constants and not of the hardness of the reaction partners is needed to predict the outcome of alkylations of the cyanide ion.[18]

Criticism

Reanalysis of various types of ambident organic system reveals that thermodynamic/kinetic control describes reactivity of organic compounds perfectly, whereas the HSAB principle fails and should be abandoned in the rationalization of ambident reactivity of organic compounds.[19]

References

Jolly, W. L. (1984). Modern Inorganic Chemistry. New York: McGraw-Hill. ISBN 978-0-07-032760-3.
E.-C. Koch, Acid-Base Interactions in Energetic Materials: I. The Hard and Soft Acids and Bases (HSAB) Principle-Insights to Reactivity and Sensitivity of Energetic Materials, Prop.,Expl.,Pyrotech. 30 2005, 5
Pearson, Ralph G. (1963). "Hard and Soft Acids and Bases". J. Am. Chem. Soc. 85 (22): 3533–3539. doi:10.1021/ja00905a001.
Pearson, Ralph G. (1968). "Hard and soft acids and bases, HSAB, part 1: Fundamental principles". J. Chem. Educ. 1968 (45): 581–586. Bibcode:1968JChEd..45..581P. doi:10.1021/ed045p581.
Pearson, Ralph G. (1968). "Hard and soft acids and bases, HSAB, part II: Underlying theories". J. Chem. Educ. 1968 (45): 643–648. Bibcode:1968JChEd..45..643P. doi:10.1021/ed045p643.
R. G. Pearson, Chemical Hardness - Applications From Molecules to Solids, Wiley-VCH, Weinheim, 1997, 198 pp
IUPAC, Glossary of terms used in theoretical organic chemistry, accessed 16 Dec 2006.
Miessler G.L. and Tarr D.A. "Inorganic Chemistry" 2nd ed. Prentice-Hall 1999, p.181-5
Robert G. Parr & Ralph G. Pearson (1983). "Absolute hardness: companion parameter to absolute electronegativity". J. Am. Chem. Soc. 105 (26): 7512–7516. doi:10.1021/ja00364a005.
Ralph G. Pearson (2005). "Chemical hardness and density functional theory" (PDF). J. Chem. Sci. 117 (5): 369–377. CiteSeerX 10.1.1.693.7436. doi:10.1007/BF02708340.
Delchev, Ya. I.; A. I. Kuleff; J. Maruani; Tz. Mineva; F. Zahariev (2006). Jean-Pierre Julien; Jean Maruani; Didier Mayou (eds.). Strutinsky's shell-correction method in the extended Kohn-Sham scheme: application to the ionization potential, electron affinity, electronegativity and chemical hardness of atoms in Recent Advances in the Theory of Chemical and Physical Systems. New York: Springer-Verlag. pp. 159–177. ISBN 978-1-4020-4527-1.
Vogel G. C.;Drago, R. S. (1996). "The ECW Model". Journal of Chemical Education. 73 (8): 701–707. Bibcode:1996JChEd..73..701V. doi:10.1021/ed073p701.CS1 maint: uses authors parameter (link)
Hancock, R. D.; Martell, A. E. (1989). "Ligand design for the selective complexation of metal ions in aqueous solution". Chemical Reviews. 89 (8): 1875–1914. doi:10.1021/cr00098a011.
Christe, K.O.; Dixon, D.A.; McLemore, D.; Wilson, W.W.; Sheehy, J.A.; Boatz, J.A. (2000). "On a quantitative scale for Lewis acidity and recent progress in polynitrogen chemistry". Journal of Fluorine Chemistry. 101 (2): 151–153. doi:10.1016/S0022-1139(99)00151-7. ISSN 0022-1139.
Laurence, C. and Gal, J-F. Lewis Basicity and Affinity Scales, Data and Measurement, (Wiley 2010) p 51 ISBN 978-0-470-74957-9
Cramer, R. E., and Bopp, T. T. (1977) Great E and C plot. Graphical display of the enthalpies of adduct formation for Lewis acids and bases. Journal of Chemical Education 54 612-613
The Mechanism of the Reaction of Silver Nitrite with Alkyl Halides. The Contrasting Reactions of Silver and Alkali Metal Salts with Alkyl Halides. The Alkylation of Ambident Anions Nathan Kornblum, Robert A. Smiley, Robert K. Blackwood, Don C. Iffland J. Am. Chem. Soc.; 1955; 77(23); 6269-6280. doi:10.1021/ja01628a064
Tishkov, Alexander A.; Mayr, Herbert (2004). "Ambident Reactivity of the Cyanide Ion: A Failure of the HSAB Principle". Angewandte Chemie International Edition. 44 (1): 142–145. doi:10.1002/anie.200461640. PMID 15599920.
Mayr, Herbert (2011). "Farewell to the HSAB Treatment of Ambident Reactivity". Angewandte Chemie International Edition. 50 (29): 6470–6505. doi:10.1002/anie.201007100. PMID 21726020.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Jolly, W. L. (1984). Modern Inorganic Chemistry. New York: McGraw-Hill. ISBN 978-0-07-032760-3.

[2] E.-C. Koch, Acid-Base Interactions in Energetic Materials: I. The Hard and Soft Acids and Bases (HSAB) Principle-Insights to Reactivity and Sensitivity of Energetic Materials, Prop.,Expl.,Pyrotech. 30 2005, 5

[3] Pearson, Ralph G. (1963). "Hard and Soft Acids and Bases". J. Am. Chem. Soc. 85 (22): 3533–3539. doi:10.1021/ja00905a001.

[4] Pearson, Ralph G. (1968). "Hard and soft acids and bases, HSAB, part 1: Fundamental principles". J. Chem. Educ. 1968 (45): 581–586. Bibcode:1968JChEd..45..581P. doi:10.1021/ed045p581.

[5] Pearson, Ralph G. (1968). "Hard and soft acids and bases, HSAB, part II: Underlying theories". J. Chem. Educ. 1968 (45): 643–648. Bibcode:1968JChEd..45..643P. doi:10.1021/ed045p643.

[6] R. G. Pearson, Chemical Hardness - Applications From Molecules to Solids, Wiley-VCH, Weinheim, 1997, 198 pp

[IUPAC-7] IUPAC, Glossary of terms used in theoretical organic chemistry, accessed 16 Dec 2006.

[Miessler-8] Miessler G.L. and Tarr D.A. "Inorganic Chemistry" 2nd ed. Prentice-Hall 1999, p.181-5

[abshardess-9] Robert G. Parr & Ralph G. Pearson (1983). "Absolute hardness: companion parameter to absolute electronegativity". J. Am. Chem. Soc. 105 (26): 7512–7516. doi:10.1021/ja00364a005.

[10] Ralph G. Pearson (2005). "Chemical hardness and density functional theory" (PDF). J. Chem. Sci. 117 (5): 369–377. CiteSeerX 10.1.1.693.7436. doi:10.1007/BF02708340.

[11] Delchev, Ya. I.; A. I. Kuleff; J. Maruani; Tz. Mineva; F. Zahariev (2006). Jean-Pierre Julien; Jean Maruani; Didier Mayou (eds.). Strutinsky's shell-correction method in the extended Kohn-Sham scheme: application to the ionization potential, electron affinity, electronegativity and chemical hardness of atoms in Recent Advances in the Theory of Chemical and Physical Systems. New York: Springer-Verlag. pp. 159–177. ISBN 978-1-4020-4527-1.

[12] Vogel G. C.;Drago, R. S. (1996). "The ECW Model". Journal of Chemical Education. 73 (8): 701–707. Bibcode:1996JChEd..73..701V. doi:10.1021/ed073p701.CS1 maint: uses authors parameter (link)

[13] Hancock, R. D.; Martell, A. E. (1989). "Ligand design for the selective complexation of metal ions in aqueous solution". Chemical Reviews. 89 (8): 1875–1914. doi:10.1021/cr00098a011.

[14] Christe, K.O.; Dixon, D.A.; McLemore, D.; Wilson, W.W.; Sheehy, J.A.; Boatz, J.A. (2000). "On a quantitative scale for Lewis acidity and recent progress in polynitrogen chemistry". Journal of Fluorine Chemistry. 101 (2): 151–153. doi:10.1016/S0022-1139(99)00151-7. ISSN 0022-1139.

[15] Laurence, C. and Gal, J-F. Lewis Basicity and Affinity Scales, Data and Measurement, (Wiley 2010) p 51 ISBN 978-0-470-74957-9

[16] Cramer, R. E., and Bopp, T. T. (1977) Great E and C plot. Graphical display of the enthalpies of adduct formation for Lewis acids and bases. Journal of Chemical Education 54 612-613

[17] The Mechanism of the Reaction of Silver Nitrite with Alkyl Halides. The Contrasting Reactions of Silver and Alkali Metal Salts with Alkyl Halides. The Alkylation of Ambident Anions Nathan Kornblum, Robert A. Smiley, Robert K. Blackwood, Don C. Iffland J. Am. Chem. Soc.; 1955; 77(23); 6269-6280. doi:10.1021/ja01628a064

[18] Tishkov, Alexander A.; Mayr, Herbert (2004). "Ambident Reactivity of the Cyanide Ion: A Failure of the HSAB Principle". Angewandte Chemie International Edition. 44 (1): 142–145. doi:10.1002/anie.200461640. PMID 15599920.

[19] Mayr, Herbert (2011). "Farewell to the HSAB Treatment of Ambident Reactivity". Angewandte Chemie International Edition. 50 (29): 6470–6505. doi:10.1002/anie.201007100. PMID 21726020.