Image rectification
Image rectification is a transformation process used to project images onto a common image plane. This process has several degrees of freedom and there are many strategies for transforming images to the common plane.
- It is used in computer stereo vision to simplify the problem of finding matching points between images (i.e. the correspondence problem).
- It is used in geographic information systems to merge images taken from multiple perspectives into a common map coordinate system.
In computer vision
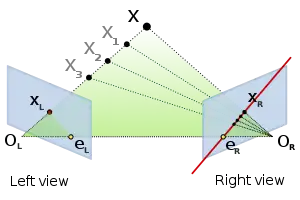
Computer stereo vision takes two or more images with known relative camera positions that show an object from different viewpoints. For each pixel it then determines the corresponding scene point's depth (i.e. distance from the camera) by first finding matching pixels (i.e. pixels showing the same scene point) in the other image(s) and then applying triangulation to the found matches to determine their depth. Finding matches in stereo vision is restricted by epipolar geometry: Each pixel's match in another image can only be found on a line called the epipolar line. If two images are coplanar, i.e. they were taken such that the right camera is only offset horizontally compared to the left camera (not being moved towards the object or rotated), then each pixel's epipolar line is horizontal and at the same vertical position as that pixel. However, in general settings (the camera did move towards the object or rotate) the epipolar lines are slanted. Image rectification warps both images such that they appear as if they have been taken with only a horizontal displacement and as a consequence all epipolar lines are horizontal, which slightly simplifies the stereo matching process. Note however, that rectification does not fundamentally change the stereo matching process: It searches on lines, slanted ones before and horizontal ones after rectification.
Image rectification is also an equivalent (and more often used[2]) alternative to perfect camera coplanarity. Even with high-precision equipment, image rectification is usually performed because it may be impractical to maintain perfect coplanarity between cameras.
Image rectification can only be performed with two images at a time and simultaneous rectification of more than two images is generally impossible.[3]
Transformation
If the images to be rectified are taken from camera pairs without geometric distortion, this calculation can easily be made with a linear transformation. X & Y rotation puts the images on the same plane, scaling makes the image frames be the same size and Z rotation & skew adjustments make the image pixel rows directly line up. The rigid alignment of the cameras needs to be known (by calibration) and the calibration coefficients are used by the transform.[4]
In performing the transform, if the cameras themselves are calibrated for internal parameters, an essential matrix provides the relationship between the cameras. The more general case (without camera calibration) is represented by the fundamental matrix. If the fundamental matrix is not known, it is necessary to find preliminary point correspondences between stereo images to facilitate its extraction.[4]
Algorithms
There are three main categories for image rectification algorithms: planar rectification,[1] cylindrical rectification[2] and polar rectification.[5][6][7]
Implementation details
All rectified images satisfy the following two properties:[8]
- All epipolar lines are parallel to the horizontal axis.
- Corresponding points have identical vertical coordinates.
In order to transform the original image pair into a rectified image pair, it is necessary to find a projective transformation H. Constraints are placed on H to satisfy the two properties above. For example, constraining the epipolar lines to be parallel with the horizontal axis means that epipoles must be mapped to the infinite point [1,0,0]T in homogeneous coordinates. Even with these constraints, H still has four degrees of freedom.[9] It is also necessary to find a matching H' to rectify the second image of an image pair. Poor choices of H and H' can result in rectified images that are dramatically changed in scale or severely distorted.
There are many different strategies for choosing a projective transform H for each image from all possible solutions. One advanced method is minimizing the disparity or least-square difference of corresponding points on the horizontal axis of the rectified image pair.[9] Another method is separating H into a specialized projective transform, similarity transform, and shearing transform to minimize image distortion.[8] One simple method is to rotate both images to look perpendicular to the line joining their collective optical centers, twist the optical axes so the horizontal axis of each image points in the direction of the other image's optical center, and finally scale the smaller image to match for line-to-line correspondence.[3] This process is demonstrated in the following example.
Example

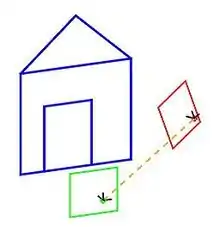
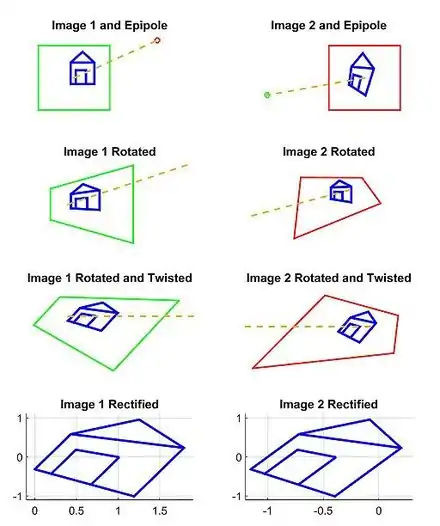
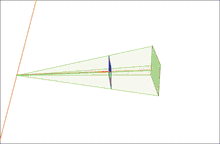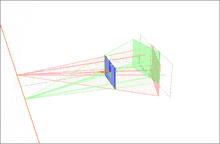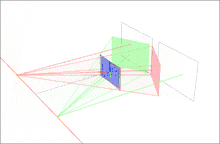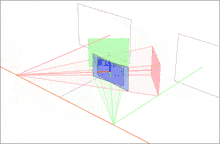
Our model for this example is based on a pair of images that observe a 3D point P, which corresponds to p and p' in the pixel coordinates of each image. O and O' represent the optical centers of each camera, with known camera matrices and (we assume the world origin is at the first camera). We will briefly outline and depict the results for a simple approach to find a H and H' projective transformation that rectify the image pair from the example scene.
First, we compute the epipoles, e and e' in each image:
Second, we find a projective transformation H1 that rotates our first image to be perpendicular to the baseline connecting O and O' (row 2, column 1 of 2D image set). This rotation can be found by using the cross product between the original and the desired optical axes.[3] Next, we find the projective transformation H2 that takes the rotated image and twists it so that the horizontal axis aligns with the baseline. If calculated correctly, this second transformation should map the e to infinity on the x axis (row 3, column 1 of 2D image set). Finally, define as the projective transformation for rectifying the first image.
Third, through an equivalent operation, we can find H' to rectify the second image (column 2 of 2D image set). Note that H'1 should rotate the second image's optical axis to be parallel with the transformed optical axis of the first image. One strategy is to pick a plane parallel to the line where the two original optical axes intersect to minimize distortion from the reprojection process.[10] In this example, we simply define H' using the rotation matrix R and initial projective transformation H as .
Finally, we scale both images to the same approximate resolution and align the now horizontal epipoles for easier horizontal scanning for correspondences (row 4 of 2D image set).
Note that it is possible to perform this and similar algorithms without having the camera parameter matrices M and M' . All that is required is a set of seven or more image to image correspondences to compute the fundamental matrices and epipoles.[9]
In geographic information system
Image rectification in GIS converts images to a standard map coordinate system. This is done by matching ground control points (GCP) in the mapping system to points in the image. These GCPs calculate necessary image transforms.[11]
Primary difficulties in the process occur
- when the accuracy of the map points are not well known
- when the images lack clearly identifiable points to correspond to the maps.
The maps that are used with rectified images are non-topographical. However, the images to be used may contain distortion from terrain. Image orthorectification additionally removes these effects.[11]
Image rectification is a standard feature available with GIS software packages.
Reference implementations
This section provides external links to reference implementations of image rectification.
- stereoRectify and stereoRectifyUncalibrated (part of OpenCV), open source for Windows, Linux/Mac, Android, and iOS
- Rectification Kit and Uncalibrated Rectification Kit, MATLAB source code with tutorial by Andrea Fusiello[4]
- rectification, part of a MATLAB package by Du Huynh with a short tutorial[12]
- rectifyStereoImages, native MATLAB function in Computer Vision System Toolbox
See also
References
- Fusiello, Andrea; Trucco, Emanuele; Verri, Alessandro (2000-03-02). "A compact algorithm for rectification of stereo pairs" (PDF). Machine Vision and Applications. 12: 16–22. doi:10.1007/s001380050120. S2CID 13250851. Retrieved 2010-06-08.
- Oram, Daniel (2001). "Rectification for Any Epipolar Geometry". Missing or empty
|url=(help) - Richard Szeliski (2010). Computer vision: Algorithms and applications. Springer. ISBN 9781848829350.
- Fusiello, Andrea (2000-03-17). "Epipolar Rectification". Retrieved 2008-06-09.
- Pollefeys, Marc; Koch, Reinhard; Van Gool, Luc (1999). "A simple and efficient rectification method for general motion" (PDF). Proc. International Conference on Computer Vision: 496–501. Retrieved 2011-01-19.
- Lim, Ser-Nam; Mittal, Anurag; Davis, Larry; Paragios, Nikos. "Uncalibrated stereo rectification for automatic 3D surveillance" (PDF). International Conference on Image Processing. 2: 1357. Archived from the original (PDF) on 2010-08-21. Retrieved 2010-06-08.
- Roberto, Rafael; Teichrieb, Veronica; Kelner, Judith (2009). "Retificação Cilíndrica: um método eficente para retificar um par de imagens" (PDF). Workshops of Sibgrapi 2009 - Undergraduate Works (in Portuguese). Archived from the original (PDF) on 2011-07-06. Retrieved 2011-03-05.
- Loop, Charles; Zhang, Zhengyou (1999). "Computing rectifying homographies for stereo vision" (PDF). Proceedings. 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149). pp. 125–131. CiteSeerX 10.1.1.34.6182. doi:10.1109/CVPR.1999.786928. ISBN 978-0-7695-0149-9. S2CID 157172. Retrieved 2014-11-09.
- Richard Hartley and Andrew Zisserman (2003). Multiple view geometry in computer vision. Cambridge university press. ISBN 9780521540513.
- David A. Forsyth and Jean Ponce (2002). Computer vision: a modern approach. Prentice Hall Professional Technical Reference.
- Fogel, David. "Image Rectification with Radial Basis Functions". Archived from the original on 2008-05-24. Retrieved 2008-06-09.
- Huynh, Du. "Polar rectification". Retrieved 2014-11-09.
- R. I. Hartley (1999). "Theory and Practice of Projective Rectification". International Journal of Computer Vision. 35 (2): 115–127. doi:10.1023/A:1008115206617. S2CID 406463.
- Pollefeys, Marc. "Polar rectification". Retrieved 2007-06-09.
- Linda G. Shapiro and George C. Stockman (2001). Computer Vision. Prentice Hall. pp. 580. ISBN 978-0-13-030796-5.
Further reading
- Computing Rectifying Homographies for Stereo Vision by Charles Loop and Zhengyou Zhang (April 8, 1999) Microsoft Research
- Computer Vision: Algorithms and Applications, Section 11.1.1 "Rectification" by Richard Szeliski (September 3, 2010) Springer
