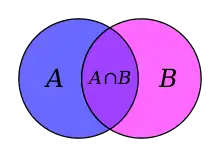
Intersection (set theory)

Intersection is written using the sign "∩" between the terms; that is, in infix notation. For example,

${\displaystyle \{1,2,3\}\cap \{2,3,4\}=\{2,3\}}$

${\displaystyle \{1,2,3\}\cap \{4,5,6\}=\emptyset }$

${\displaystyle \mathbb {Z} \cap \mathbb {N} =\mathbb {N} }$

${\displaystyle \{x\in \mathbb {R} :x^{2}=1\}\cap \mathbb {N} =\{1\}}$

The intersection of more than two sets (generalized intersection) can be written as[1]

${\displaystyle \bigcap _{i=1}^{n}A_{i}}$

which is similar to capital-sigma notation.

For an explanation of the symbols used in this article, refer to the table of mathematical symbols.

Intersection of three sets:
${\displaystyle ~A\cap B\cap C}$

Intersections of the Greek, Latin and Russian alphabet, considering only the shapes of the letters and ignoring their pronunciation

Example of an intersection with sets

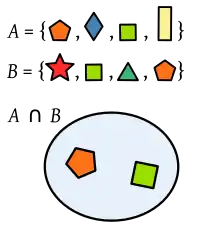
The intersection of two sets A and B, denoted by A ∩ B,[1][4] is the set of all objects that are members of both the sets A and B. In symbols,

${\displaystyle A\cap B=\{x:x\in A{\text{ and }}x\in B\}.}$

That is, x is an element of the intersection A ∩ B, if and only if x is both an element of A and an element of B.[4]

For example:

• The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
• The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, ...} and the set of odd numbers {1, 3, 5, 7, 9, 11, ...}, because 9 is not prime.

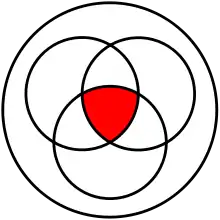
Intersection is an associative operation; that is, for any sets A, B, and C, one has A ∩ (B ∩ C) = (A ∩ B) ∩ C. Intersection is also commutative; for any A and B, one has A ∩ B = B ∩ A. It thus makes sense to talk about intersections of multiple sets. The intersection of A, B, C, and D, for example, is unambiguously written A ∩ B ∩ C ∩ D.

Inside a universe U, one may define the complement A^c of A to be the set of all elements of U not in A. Furthermore, the intersection of A and B may be written as the complement of the union of their complements, derived easily from De Morgan's laws:
A ∩ B = (A^c ∪ B^c)^c

The most general notion is the intersection of an arbitrary nonempty collection of sets. If M is a nonempty set whose elements are themselves sets, then x is an element of the intersection of M if and only if for every element A of M, x is an element of A. In symbols:

${\displaystyle \left(x\in \bigcap _{A\in M}A\right)\Leftrightarrow \left(\forall A\in M,\ x\in A\right).}$

The notation for this last concept can vary considerably. Set theorists will sometimes write "⋂M", while others will instead write "⋂_A∈M A". The latter notation can be generalized to "⋂_i∈I A_i", which refers to the intersection of the collection {A_i : i ∈ I}. Here I is a nonempty set, and A_i is a set for every i in I.

In the case that the index set I is the set of natural numbers, notation analogous to that of an infinite product may be seen:

${\displaystyle \bigcap _{i=1}^{\infty }A_{i}.}$

When formatting is difficult, this can also be written "A₁ ∩ A₂ ∩ A₃ ∩ ...". This last example, an intersection of countably many sets, is actually very common; for an example, see the article on σ-algebras.

Conjunctions of the arguments in parentheses

The conjunction of no argument is the tautology (compare: empty product); accordingly the intersection of no set is the universe.

Note that in the previous section, we excluded the case where M was the empty set (∅). The reason is as follows: The intersection of the collection M is defined as the set (see set-builder notation)

${\displaystyle \bigcap _{A\in M}A=\{x:\forall A\in M,x\in A\}.}$

If M is empty, there are no sets A in M, so the question becomes "which x's satisfy the stated condition?" The answer seems to be every possible x. When M is empty, the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the universal set (the identity element for the operation of intersection),[5] but in standard (ZFC) set theory, the universal set does not exist.

Wikimedia Commons has media related to Intersection (set theory).

• Algebra of sets
• Cardinality
• Complement
• Intersection graph
• Iterated binary operation
• List of set identities and relations
• Logical conjunction
• MinHash
• Naive set theory
• Symmetric difference
• Union

• Devlin, K. J. (1993). The Joy of Sets: Fundamentals of Contemporary Set Theory (Second ed.). New York, NY: Springer-Verlag. ISBN 3-540-94094-4.
• Munkres, James R. (2000). "Set Theory and Logic". Topology (Second ed.). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2.
• Rosen, Kenneth (2007). "Basic Structures: Sets, Functions, Sequences, and Sums". Discrete Mathematics and Its Applications (Sixth ed.). Boston: McGraw-Hill. ISBN 978-0-07-322972-0.

• Weisstein, Eric W. "Intersection". MathWorld.