Jacket matrix

In mathematics, a jacket matrix is a square symmetric matrix $A=(a_{ij})$ of order n if its entries are non-zero and real, complex, or from a finite field, and

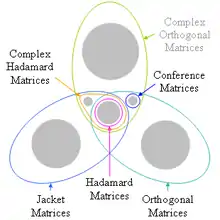
Hierarchy of matrix types

\ AB=BA=I_{n}

where I_n is the identity matrix, and

\ B={1 \over n}(a_{ij}^{-1})^{T}.

where T denotes the transpose of the matrix.

In other words, the inverse of a jacket matrix is determined its element-wise or block-wise inverse. The definition above may also be expressed as:

\forall u,v\in \{1,2,\dots ,n\}:~a_{iu},a_{iv}\neq 0,~~~~\sum _{i=1}^{n}a_{iu}^{-1}\,a_{iv}={\begin{cases}n,&u=v\\0,&u\neq v\end{cases}}

The jacket matrix is a generalization of the Hadamard matrix, also it is a Diagonal block-wise inverse matrix.

Motivation

n	.... -2, -1, 0 1, 2,.....	logarithm
2^n	.... $\ {1 \over 4},{1 \over 2},$ 1, 2, 4,.....	Series

As shown in Table, i.e. in series, n=2 case, Forward: $2^{2}=4$ , Inverse : $(2^{2})^{-1}={1 \over 4}$ , then, $4*{1 \over 4}=1$ .

Therefore, exist an element-wise inverse.

Example 1.

A=\left[{\begin{array}{rrrr}1&1&1&1\\1&-2&2&-1\\1&2&-2&-1\\1&-1&-1&1\\\end{array}}\right],

:

B={1 \over 4}\left[{\begin{array}{rrrr}1&1&1&1\\[6pt]1&-{1 \over 2}&{1 \over 2}&-1\\[6pt]1&{1 \over 2}&-{1 \over 2}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right].

or more general

A=\left[{\begin{array}{rrrr}a&b&b&a\\b&-c&c&-b\\b&c&-c&-b\\a&-b&-b&a\end{array}}\right],

:

B={1 \over 4}\left[{\begin{array}{rrrr}{1 \over a}&{1 \over b}&{1 \over b}&{1 \over a}\\[6pt]{1 \over b}&-{1 \over c}&{1 \over c}&-{1 \over b}\\[6pt]{1 \over b}&{1 \over c}&-{1 \over c}&-{1 \over b}\\[6pt]{1 \over a}&-{1 \over b}&-{1 \over b}&{1 \over a}\end{array}}\right],

Example 2.

For m x m matrices, $\mathbf {A_{j}} ,$

$\mathbf {A_{j}} =diag(A_{1},A_{2},..A_{n})$ denotes an mn x mn block diagonal Jacket matrix.

J_{4}=\left[{\begin{array}{rrrr}I_{2}&0&0&0\\0&cos\theta &-sin\theta &0\\0&sin\theta &cos\theta &0\\0&0&0&I_{2}\end{array}}\right],

\ J_{4}^{T}J_{4}=J_{4}J_{4}^{T}=I_{4}.

Example 3.

Euler's Formula:

e^{i\pi }+1=0

,

e^{i\pi }=\cos {\pi }+i\sin {\pi }=-1

and

e^{-i\pi }=\cos {\pi }-i\sin {\pi }=-1

.

Therefore,

e^{i\pi }e^{-i\pi }=(-1)({\frac {1}{-1}})=1

.

Also,

y=e^{x}

${\frac {dy}{dx}}=e^{x}$ , ${\frac {dy}{dx}}{\frac {dx}{dy}}=e^{x}{\frac {1}{e^{x}}}=1$ .

Finally,

A·B=B·A=I

References

Moon Ho Lee, "The Center Weighted Hadamard Transform", IEEE Transactions on Circuits Syst. Vol. 36, No. 9, PP. 1247–1249, Sept.1989.
K.J. Horadam, Hadamard Matrices and Their Applications, Princeton University Press, UK, Chapter 4.5.1: The jacket matrix construction, PP. 85–91, 2007.
Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing, LAP LAMBERT Publishing, Germany,Nov. 2012.

External links

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.