McGee graph
In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.[1]
| McGee graph | |
|---|---|
 The McGee graph | |
| Named after | W. F. McGee |
| Vertices | 24 |
| Edges | 36 |
| Radius | 4 |
| Diameter | 4[1] |
| Girth | 7[1] |
| Automorphisms | 32[1] |
| Chromatic number | 3[1] |
| Chromatic index | 3[1] |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Cubic Cage Hamiltonian |
| Table of graphs and parameters | |
The McGee graph is the unique (3,7)-cage (the smallest cubic graph of girth 7). It is also the smallest cubic cage that is not a Moore graph.
First discovered by Sachs but unpublished,[2] the graph is named after McGee who published the result in 1960.[3] Then, the McGee graph was proven the unique (3,7)-cage by Tutte in 1966.[4][5][6]
The McGee graph requires at least eight crossings in any drawing of it in the plane. It is one of five non-isomorphic graphs tied for being the smallest cubic graph that requires eight crossings. Another of these five graphs is the generalized Petersen graph G(12,5), also known as the Nauru graph.[7][8]
The McGee graph has radius 4, diameter 4, chromatic number 3 and chromatic index 3. It is also a 3-vertex-connected and a 3-edge-connected graph. It has book thickness 3 and queue number 2.[9]
Algebraic properties
The characteristic polynomial of the McGee graph is
- .
The automorphism group of the McGee graph is of order 32 and doesn't act transitively upon its vertices: there are two vertex orbits, of lengths 8 and 16. The McGee graph is the smallest cubic cage that is not a vertex-transitive graph.[10]
Gallery
 The crossing number of the McGee graph is 8.
The crossing number of the McGee graph is 8.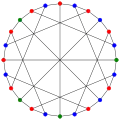 The chromatic number of the McGee graph is 3.
The chromatic number of the McGee graph is 3.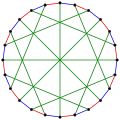 The chromatic index of the McGee graph is 3.
The chromatic index of the McGee graph is 3.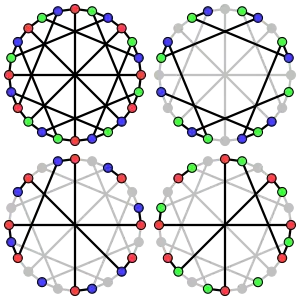 The acyclic chromatic number of the McGee graph is 3.
The acyclic chromatic number of the McGee graph is 3. Alternative drawing of the McGee graph.
Alternative drawing of the McGee graph.
References
- Weisstein, Eric W. "McGee Graph". MathWorld.
- Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
- McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
- Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
- Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982
- Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
- Sloane, N. J. A. (ed.). "Sequence A110507 (Number of nodes in the smallest cubic graph with crossing number n)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Pegg, E. T.; Exoo, G. (2009), "Crossing number graphs", Mathematica Journal, 11.
- Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
