Minifloat

In computing, minifloats are floating-point values represented with very few bits. Predictably, they are not well suited for general-purpose numerical calculations. They are used for special purposes, most often in computer graphics, where iterations are small and precision has aesthetic effects. Machine learning also uses similar formats like bfloat16. Additionally, they are frequently encountered as a pedagogical tool in computer-science courses to demonstrate the properties and structures of floating-point arithmetic and IEEE 754 numbers.

Floating-point formats
IEEE 754
Other
Computer architecture bit widths
Bit
Application
Binary floating-point precision
Decimal floating point precision

Minifloats with 16 bits are half-precision numbers (opposed to single and double precision). There are also minifloats with 8 bits or even fewer.

Minifloats can be designed following the principles of the IEEE 754 standard. In this case they must obey the (not explicitly written) rules for the frontier between subnormal and normal numbers and must have special patterns for infinity and NaN. Normalized numbers are stored with a biased exponent. The new revision of the standard, IEEE 754-2008, has 16-bit binary minifloats.

The Radeon R300 and R420 GPUs used an "fp24" floating-point format with 7 bits of exponent and 16 bits (+1 implicit) of mantissa.[1] "Full Precision" in Direct3D 9.0 is a proprietary 24-bit floating-point format. Microsoft's D3D9 (Shader Model 2.0) graphics API initially supported both FP24 (as in ATI's R300 chip) and FP32 (as in Nvidia's NV30 chip) as "Full Precision", as well as FP16 as "Partial Precision" for vertex and pixel shader calculations performed by the graphics hardware.

Notation

A minifloat is usually described using a tuple of four numbers, (S, E, M, B):

  • S is the length of the sign field. It is usually either 0 or 1.
  • E is the length of the exponent field.
  • M is the length of the mantissa (significand) field.
  • B is the exponent bias.

A minifloat format denoted by (S, E, M, B) is, therefore, S + E + M bits long.

In computer graphics minifloats are sometimes used to represent only integral values. If at the same time subnormal values should exist, the least subnormal number has to be 1. The bias value would be B = E - M - 1 in this case, assuming two special exponent values are used per IEEE.

The (S, E, M, B) notation can be converted to a (B, P, L, U) format as (2, M + 1, B + 1, 2S - B) (with IEEE use of exponents).

Example
Layout of an example 8-bit minifloat (1.4.3.−2)
sign exponent significand
7 6 5 4 3 2 1 0

In this example, a minifloat in 1 byte (8 bit) with 1 sign bit, 4 exponent bits and 3 significand bits (in short, a 1.4.3.−2 minifloat) is used to represent integral values. All IEEE 754 principles should be valid. The only free value is the exponent bias, which we define as -2 for integers. The unknown exponent is called for the moment x.

Numbers in a different base are marked as ...base, for example, 1012 = 5. The bit patterns have spaces to visualize their parts.

Representation of zero

 
0 0000 000 = 0

Subnormal numbers

The significand is extended with "0.":

0 0000 001 = 0.0012 × 2x = 0.125 × 2x = 1 (least subnormal number)
...
0 0000 111 = 0.1112 × 2x = 0.875 × 2x = 7 (greatest subnormal number)

Normalized numbers

The significand is extended with "1.":

0 0001 000 = 1.0002 × 2x = 1 × 2x = 8 (least normalized number)
0 0001 001 = 1.0012 × 2x = 1.125 × 2x = 9
...
0 0010 000 = 1.0002 × 2x+1 = 1 × 2x+1 = 16
0 0010 001 = 1.0012 × 2x+1 = 1.125 × 2x+1 = 18
...
0 1110 000 = 1.0002 × 2x+13 =  1.000 × 2x+13 =  65536
0 1110 001 = 1.0012 × 2x+13 =  1.125 × 2x+13 =  73728
...
0 1110 110 = 1.1102 × 2x+13 =  1.750 × 2x+13 = 114688
0 1110 111 = 1.1112 × 2x+13 =  1.875 × 2x+13 = 122880 (greatest normalized number)

Infinity

 
0 1111 000 = +infinity
1 1111 000 = −infinity

If the exponent field were not treated specially, the value would be

0 1111 000 = 1.0002 × 2x+14 =  217 = 131072

Not a number

 
x 1111 yyy = NaN (if yyy ≠ 000)

Without the IEEE 754 special handling of the largest exponent, the greatest possible value would be

0 1111 111 = 1.1112 × 2x+14 =  1.875 × 217 = 245760

Value of the bias

If the least subnormal value (second line above) should be 1, the value of x has to be x = 3. Therefore, the bias has to be −2; that is, every stored exponent has to be decreased by −2 or has to be increased by 2, to get the numerical exponent.

All values as decimals

This is a chart of all possible values when treating the float similarly to an IEEE float.

... 000... 001... 010... 011... 100... 101... 110... 111
0 0000 ... 00.1250.250.3750.50.6250.750.875
0 0001 ... 11.1251.251.3751.51.6251.751.875
0 0010 ... 22.252.52.7533.253.53.75
0 0011 ... 44.555.566.577.5
0 0100 ... 89101112131415
0 0101 ... 1618202224262830
0 0110 ... 3236404448525660
0 0111 ... 6472808896104112120
0 1000 ... 128144160176192208224240
0 1001 ... 256288320352384416448480
0 1010 ... 512576640704768832896960
0 1011 ... 10241152128014081536166417921920
0 1100 ... 20482304256028163072332835843840
0 1101 ... 40964608512056326144665671687680
0 1110 ... 81929216102401126412288133121433615360
0 1111 ... InfNaNNaNNaNNaNNaNNaNNaN
1 0000 ... -0-0.125-0.25-0.375-0.5-0.625-0.75-0.875
1 0001 ... -1-1.125-1.25-1.375-1.5-1.625-1.75-1.875
1 0010 ... -2-2.25-2.5-2.75-3-3.25-3.5-3.75
1 0011 ... -4-4.5-5-5.5-6-6.5-7-7.5
1 0100 ... −8−9−10−11−12−13−14−15
1 0101 ... −16−18−20−22−24−26−28−30
1 0110 ... −32−36−40−44−48−52−56−60
1 0111 ... −64−72−80−88−96−104−112−120
1 1000 ... −128−144−160−176−192−208−224−240
1 1001 ... −256−288−320−352−384−416−448−480
1 1010 ... −512−576−640−704−768−832−896−960
1 1011 ... −1024−1152−1280−1408−1536−1664−1792−1920
1 1100 ... −2048−2304−2560−2816−3072−3328−3584−3840
1 1101 ... −4096−4608−5120−5632−6144−6656−7168−7680
1 1110 ... −8192−9216−10240−11264−12288−13312−14336−15360
1 1111 ... −InfNaNNaNNaNNaNNaNNaNNaN

All values as integers

Due to the severe lack of precision with 8-bit floats, it is suggested that you only use them scaled to integer values.

... 000... 001... 010... 011... 100... 101... 110... 111
0 0000 ... 01234567
0 0001 ... 89101112131415
0 0010 ... 1618202224262830
0 0011 ... 3236404448525660
0 0100 ... 6472808896104112120
0 0101 ... 128144160176192208224240
0 0110 ... 256288320352384416448480
0 0111 ... 512576640704768832896960
0 1000 ... 10241152128014081536166417921920
0 1001 ... 20482304256028163072332835843840
0 1010 ... 40964608512056326144665671687680
0 1011 ... 81929216102401126412288133121433615360
0 1100 ... 1638418432204802252824576266242867230720
0 1101 ... 3276836864409604505649152532485734461440
0 1110 ... 6553673728819209011298304106496114688122880
0 1111 ... InfNaNNaNNaNNaNNaNNaNNaN
1 0000 ... −0−1−2−3−4−5−6−7
1 0001 ... −8−9−10−11−12−13−14−15
1 0010 ... −16−18−20−22−24−26−28−30
1 0011 ... −32−36−40−44−48−52−56−60
1 0100 ... −64−72−80−88−96−104−112−120
1 0101 ... −128−144−160−176−192−208−224−240
1 0110 ... −256−288−320−352−384−416−448−480
1 0111 ... −512−576−640−704−768−832−896−960
1 1000 ... −1024−1152−1280−1408−1536−1664−1792−1920
1 1001 ... −2048−2304−2560−2816−3072−3328−3584−3840
1 1010 ... −4096−4608−5120−5632−6144−6656−7168−7680
1 1011 ... −8192−9216−10240−11264−12288−13312−14336−15360
1 1100 ... −16384−18432−20480−22528−24576−26624−28672−30720
1 1101 ... −32768−36864−40960−45056−49152−53248−57344−61440
1 1110 ... −65536−73728−81920−90112−98304−106496−114688−122880
1 1111 ... −InfNaNNaNNaNNaNNaNNaNNaN

However, in practice, floats are not shown exactly. Instead, they are rounded; for example, if a float had about 3 significant digits, and the number 8192 was represented, it would be rounded to 8190 to avoid false precision, otherwise a number like 1000000 converted to such a float and back would be confusingly shown as, for example, 1000448.

Properties of this example
Graphical representation of integral (1.4.3.−2) minifloats

Integral minifloats in 1 byte have a greater range of ±122 880 than two's-complement integer with a range −128 to +127. The greater range is compensated by a poor precision, because there are only 4 mantissa bits, equivalent to slightly more than one decimal place. They also have greater range than half-precision minifloats with range ±65 504, also compensated by lack of fractions and poor precision.

There are only 242 different values (if +0 and −0 are regarded as different), because 14 of the bit patterns represent NaNs.

The values between 0 and 16 have the same bit pattern as minifloat or two's-complement integer. The first pattern with a different value is 00010001, which is 18 as a minifloat and 17 as a two's-complement integer.

This coincidence does not occur at all with negative values, because this minifloat is a signed-magnitude format.

The (vertical) real line on the right shows clearly the varying density of the floating-point values – a property which is common to any floating-point system. This varying density results in a curve similar to the exponential function.

Although the curve may appear smooth, this is not the case. The graph actually consists of distinct points, and these points lie on line segments with discrete slopes. The value of the exponent bits determines the absolute precision of the mantissa bits, and it is this precision that determines the slope of each linear segment.

Arithmetic

Addition
Addition of (1.3.2.3)-minifloats

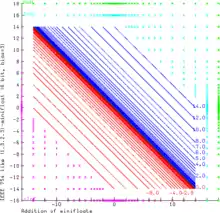
The graphic demonstrates the addition of even smaller (1.3.2.3)-minifloats with 6 bits. This floating-point system follows the rules of IEEE 754 exactly. NaN as operand produces always NaN results. Inf − Inf and (−Inf) + Inf results in NaN too (green area). Inf can be augmented and decremented by finite values without change. Sums with finite operands can give an infinite result (i.e. 14.0 + 3.0 = +Inf as a result is the cyan area, −Inf is the magenta area). The range of the finite operands is filled with the curves x + y = c, where c is always one of the representable float values (blue and red for positive and negative results respectively).

Subtraction, multiplication and division

The other arithmetic operations can be illustrated similarly:

  • Subtraction
  • Multiplication
  • Division

In embedded devices

Minifloats are also commonly used in embedded devices, especially on microcontrollers where floating-point will need to be emulated in software anyways. To speed up the computation, the mantissa typically occupies exactly half of the bits, so the register boundary automatically addresses the parts without shifting.

See also

References
  1. Buck, Ian (13 March 2005), "Chapter 32. Taking the Plunge into GPU Computing", in Pharr, Matt (ed.), GPU Gems, ISBN 0-321-33559-7, retrieved 5 April 2018.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.