Mittag-Leffler function

In mathematics, the Mittag-Leffler function E_α,β is a special function, a complex function which depends on two complex parameters α and β. It may be defined by the following series when the real part of α is strictly positive:[1][2]

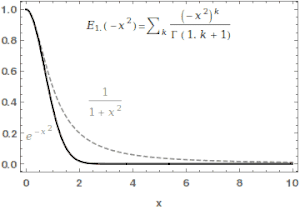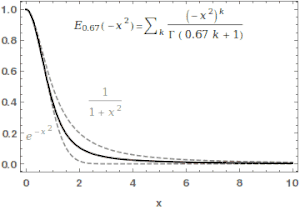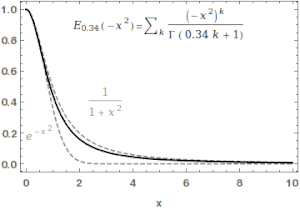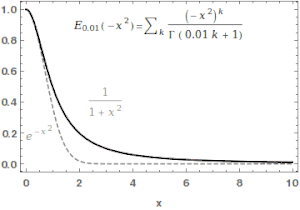
E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (\alpha k+\beta )}}.

The Mittag-Leffler function can be used to interpolate continuously between a Gaussian and a Lorentzian function.

where $\Gamma (x)$ is the gamma function. When $\beta =1$ , it is abbreviated as $E_{\alpha }(z)=E_{\alpha ,1}(z)$ . For $\alpha =0$ , the series above equals the Taylor expansion of the geometric series and consequently $E_{0,\beta }(z)={\frac {1}{\Gamma (\beta )}}{\frac {1}{1-z}}$ .

In the case α and β are real and positive, the series converges for all values of the argument z, so the Mittag-Leffler function is an entire function. This function is named after Gösta Mittag-Leffler. This class of functions are important in the theory of the fractional calculus.

For α > 0, the Mittag-Leffler function $E_{\alpha ,1}(z)$ is an entire function of order 1/α, and is in some sense the simplest entire function of its order.

The Mittag-Leffler function satisfies the recurrence property (Theorem 5.1 of [1])

E_{\alpha ,\beta }(z)={\frac {1}{z}}E_{\alpha ,\beta -\alpha }(z)-{\frac {1}{z\Gamma (\beta -\alpha ),}}

from which the Poincaré asymptotic expansion

E_{\alpha ,\beta }(z)\sim -\sum _{k=1}{\frac {1}{z^{k}\Gamma (\beta -k\alpha )}}

follows, which is true for $z\to -\infty$ .

Special cases

For $\alpha =0,1/2,1,2$ we find: (Section 2 of [1])

Error function:

E_{\frac {1}{2}}(z)=\exp(z^{2})\operatorname {erfc} (-z).

The sum of a geometric progression:

E_{0}(z)=\sum _{k=0}^{\infty }z^{k}={\frac {1}{1-z}},\,|z|<1.

Exponential function:

E_{1}(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (k+1)}}=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}=\exp(z).

Hyperbolic cosine:

E_{2}(z)=\cosh({\sqrt {z}}),{\text{ and }}E_{2}(-z^{2})=\cos(z).

For $\beta =2$ , we have

E_{1,2}(z)={\frac {e^{z}-1}{z}},

E_{2,2}(z)={\frac {\sinh({\sqrt {z}})}{\sqrt {z}}}.

For $\alpha =0,1,2$ , the integral

\int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d} }s

gives, respectively: $\arctan(z)$ , ${\tfrac {\sqrt {\pi }}{2}}\operatorname {erf} (z)$ , $\sin(z)$ .

Mittag-Leffler's integral representation

The integral representation of the Mittag-Leffler function is (Section 6 of [1])

E_{\alpha ,\beta }(z)={\frac {1}{2\pi i}}\int _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,

where the contour C starts and ends at −∞ and circles around the singularities and branch points of the integrand.

Related to the Laplace transform and Mittag-Leffler summation is the expression (Eq (7.5) of,[1] with m=0)

\int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.

Notes

R Package 'MittagLeffleR' by Gurtek Gill, Peter Straka. Implements the Mittag-Leffler function, distribution, random variate generation, and estimation.

References

Saxena, R. K.; Mathai, A. M.; Haubold, H. J. (2009-09-01). "Mittag-Leffler Functions and Their Applications". arXiv:0909.0230v2. Cite journal requires |journal= (help)
Weisstein, Eric W. "Mittag-Leffler Function". mathworld.wolfram.com. Retrieved 2019-09-11.

Mittag-Leffler, M.G.: Sur la nouvelle fonction E(x). C. R. Acad. Sci. Paris 137, 554–558 (1903)
Mittag-Leffler, M.G.: Sopra la funzione E˛.x/. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904)
Gorenflo R., Kilbas A.A., Mainardi F., Rogosin S.V., Mittag-Leffler Functions, Related Topics and Applications (Springer, New York, 2014) 443 pages ISBN 978-3-662-43929-6
Igor Podlubny (1998). "chapter 1". Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering. Academic Press. ISBN 0-12-558840-2.
Kai Diethelm (2010). "chapter 4". The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type. Lecture Notes in Mathematics. Heidelberg and New York: Springer-Verlag. ISBN 978-3-642-14573-5.

External links

This article incorporates material from Mittag-Leffler function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Saxena, R. K.; Mathai, A. M.; Haubold, H. J. (2009-09-01). "Mittag-Leffler Functions and Their Applications". arXiv:0909.0230v2. Cite journal requires |journal= (help)

[2] Weisstein, Eric W. "Mittag-Leffler Function". mathworld.wolfram.com. Retrieved 2019-09-11.