Mycielskian

Mycielskian construction applied to a 5-cycle graph, producing the Grötzsch graph with 11 vertices and 20 edges, the smallest triangle-free 4-chromatic graph (Chvátal 1974).

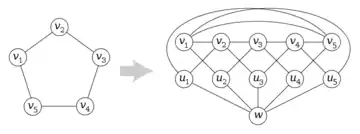
Let the n vertices of the given graph G be v₁, v₂, . . . , v_n. The Mycielski graph μ(G) contains G itself as a subgraph, together with n+1 additional vertices: a vertex u_i corresponding to each vertex v_i of G, and an extra vertex w. Each vertex u_i is connected by an edge to w, so that these vertices form a subgraph in the form of a star K_1,n. In addition, for each edge v_iv_j of G, the Mycielski graph includes two edges, u_iv_j and v_iu_j.

Thus, if G has n vertices and m edges, μ(G) has 2n+1 vertices and 3m+n edges.

The only new triangles in μ(G) are of the form v_iv_ju_k, where v_iv_jv_k is a triangle in G. Thus, if G is triangle-free, so is μ(G).

To see that the construction increases the chromatic number ${\displaystyle \chi (G)=k}$, consider a proper k-coloring of ${\displaystyle \mu (G){-}\{w\}}$; that is, a mapping ${\displaystyle c:\{v_{1},\ldots ,v_{n},u_{1},\ldots ,u_{n}\}\to \{1,2,\ldots ,k\}}$ with ${\displaystyle c(x)\neq c(y)}$ for adjacent vertices x,y. If we had ${\displaystyle c(u_{i})\subset \{1,2,\ldots ,k{-}1\}}$ for all i, then we could define a proper (k−1)-coloring of G by ${\displaystyle c'\!(v_{i})=c(u_{i})}$ when ${\displaystyle c(v_{i})=k}$, and ${\displaystyle c'\!(v_{i})=c(v_{i})}$ otherwise. But this is impossible for ${\displaystyle \chi (G)=k}$, so c must use all k colors for ${\displaystyle \{u_{1},\ldots ,u_{n}\}}$, and any proper coloring of the last vertex w must use an extra color. That is, ${\displaystyle \chi (\mu (G))=k{+}1}$.

M₂, M₃ and M₄ Mycielski graphs

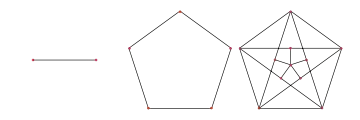
Applying the Mycielskian repeatedly, starting with the one-edge graph, produces a sequence of graphs M_i = μ(M_i−1), sometimes called the Mycielski graphs. The first few graphs in this sequence are the graph M₂ = K₂ with two vertices connected by an edge, the cycle graph M₃ = C₅, and the Grötzsch graph M₄ with 11 vertices and 20 edges.

In general, the graph M_i is triangle-free, (i−1)-vertex-connected, and i-chromatic. The number of vertices in M_i for i ≥ 2 is 3 × 2ⁱ⁻² − 1 (sequence A083329 in the OEIS), while the number of edges for i = 2, 3, . . . is:

1, 5, 20, 71, 236, 755, 2360, 7271, 22196, 67355, ... (sequence A122695 in the OEIS).

Hamiltonian cycle in M₄ (Grötzsch graph)

• If G has chromatic number k, then μ(G) has chromatic number k + 1 (Mycielski 1955).
• If G is triangle-free, then so is μ(G) (Mycielski 1955).
• More generally, if G has clique number ω(G), then μ(G) has clique number max(2,ω(G)).(Mycielski 1955).
• If G is a factor-critical graph, then so is μ(G) (Došlić 2005). In particular, every graph M_i for i ≥ 2 is factor-critical.
• If G has a Hamiltonian cycle, then so does μ(G) (Fisher, McKenna & Boyer 1998).
• If G has domination number γ(G), then μ(G) has domination number γ(G)+1. (Fisher, McKenna & Boyer 1998).

A generalized Mycielskian, formed as a cone over the 5-cycle, Δ₃(C₅) = Δ₃(Δ₂(K₂)).

A generalization of the Mycielskian, called a cone over a graph, was introduced by Stiebitz (1985) and further studied by Tardif (2001) and Lin et al. (2006). In this construction, one forms a graph Δ_i(G) from a given graph G by taking the tensor product of graphs G × H, where H is a path of length i with a self-loop at one end, and then collapsing into a single supervertex all of the vertices associated with the vertex of H at the non-loop end of the path. The Mycielskian itself can be formed in this way as μ(G) = Δ₂(G).

While the cone construction does not always increase the chromatic number, Stiebitz (1985) proved that it does so when applied iteratively to K₂. That is, define a sequence of families of graphs, called generalized Mycielskians, as

ℳ(2) = {K₂} and ℳ(k+1) = {Δ_i(G) | G ∈ ℳ(k), i ∈ ℕ}.

For example, ℳ(3) is the family of odd cycles. Then each graph in ℳ(k) is k-chromatic. The proof uses methods of topological combinatorics developed by László Lovász to compute the chromatic number of Kneser graphs. The triangle-free property is then strengthened as follows: if one only applies the cone construction Δ_i for i ≥ r, then the resulting graph has odd girth at least 2r + 1, that is, it contains no odd cycles of length less than 2r + 1. Thus generalized Mycielskians provide a simple construction of graphs with high chromatic number and high odd girth.

• Chvátal, Vašek (1974), "The minimality of the Mycielski graph", Graphs and Combinatorics (Proc. Capital Conf., George Washington Univ., Washington, D.C., 1973), Lecture Notes in Mathematics, 406, Springer-Verlag, pp. 243–246.
• Došlić, Tomislav (2005), "Mycielskians and matchings", Discussiones Mathematicae Graph Theory, 25 (3): 261–266, doi:10.7151/dmgt.1279, MR 2232992.
• Fisher, David C.; McKenna, Patricia A.; Boyer, Elizabeth D. (1998), "Hamiltonicity, diameter, domination, packing, and biclique partitions of Mycielski's graphs", Discrete Applied Mathematics, 84 (1–3): 93–105, doi:10.1016/S0166-218X(97)00126-1.
• Lin, Wensong; Wu, Jianzhuan; Lam, Peter Che Bor; Gu, Guohua (2006), "Several parameters of generalized Mycielskians", Discrete Applied Mathematics, 154 (8): 1173–1182, doi:10.1016/j.dam.2005.11.001.
• Mycielski, Jan (1955), "Sur le coloriage des graphes" (PDF), Colloq. Math., 3: 161–162.
• Stiebitz, M. (1985), Beiträge zur Theorie der färbungskritschen Graphen, Habilitation thesis, Technische Universität Ilmenau. As cited by Tardif (2001).
• Tardif, C. (2001), "Fractional chromatic numbers of cones over graphs", Journal of Graph Theory, 38 (2): 87–94, doi:10.1002/jgt.1025.

• Weisstein, Eric W. "Mycielski Graph". MathWorld.