Nonlinear frictiophoresis
Nonlinear frictiophoresis is the unidirectional drift of a particle in a medium caused by periodic driving force with zero mean. The effect is possible due to nonlinear dependence of the friction-drag force on the particle's velocity. It was discovered theoretically.,[1] and is mainly known as nonlinear electrofrictiophoresis [1] .[2] At first glance, a periodic driving force with zero mean is able to entrain a particle into an oscillating movement without unidirectional drift, because integral momentum provided to the particle by the force is zero. The possibility of unidirectional drift can be recognized if one takes into account that the particle itself loses momentum through transferring it further to the medium it moves in/at. If the friction is nonlinear, then it may so happen that the momentum loss during movement in one direction does not equal to that in the opposite direction and this causes unidirectional drift. For this to happen, the driving force time-dependence must be more complicated than it is in a single sinusoidal harmonic.
A simple example - Bingham plastic
Nonlinear friction
The simplest case of friction-velocity dependence law is the Stokes's one:
where is the friction/drag force applied to a particle moving with velocity in a medium. The friction-velocity law (1) is observed for a slowly moving spherical particle in a Newtonian fluid.
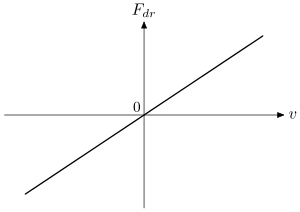
It is linear, see Fig. 1, and is not suitable for nonlinear frictiophoresis to take place. The characteristic property of the law (1) is that any, even a very small driving force is able to get particle moving. This is not the case for such media as Bingham plastic. For those media, it is necessary to apply some threshold force, , to get the particle moving. This kind of friction-velocity (dry friction) law has a jump discontinuity at :

It is nonlinear, see Fig. 2, and is used in this example.
Periodic driving force
Let denote the period of driving force. Chose a time value such that and two force values, , such that the following relations are satisfied:
The periodic driving force used in this example is as follows:
It is clear that, due to (3), has zero mean:
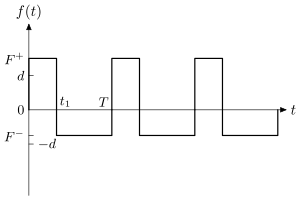
See also Fig. 3.
Unidirectional drift
For the sake of simplicity, we consider here the physical situation when inertia may be neglected. The latter can be achieved if particle's mass is small, velocity is low and friction is high. This conditions have to ensure that , where is the relaxation time. In this situation, the particle driven with force (4) immediately starts moving with constant velocity during interval and will immediately stop moving during interval , see Fig. 4.
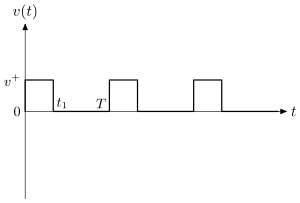
This results in the positive mean velocity of unidirectional drift:
Mathematical analysis
Analysis of possibility to get a nonzero drift by periodic force with zero integral has been made in .[1] The dimensionless equation of motion for a particle driven by periodic force , , is as follows:
where the friction/drag force satisfies the following:
It is proven in [1] that any solution to (5) settles down onto periodic regime , , which has nonzero mean:
almost certainly, provided is not antiperiodic.[3]
For , two cases of have been considered explicitly:
1. Saw-shaped driving force, see Fig. 5:
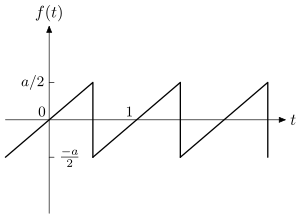
In this case, found in [1] first order in approximation to , , has the following mean value:
This estimate is made expecting .
2. Two harmonics driving force,
In this case, the first order in approximation has the following mean value:
This value is maximized in , , keeping constant. Interesting that the drift value depends on and changes its direction twice as spans over the interval . Another type of analysis,[4] based on symmetry breaking suggests as well that a zero mean driving force is able to generate a directed drift.
Applications

In applications, the nature of force in (5), is usually electric, similar to forces acting during standard electrophoresis. The only differences are that the force is periodic and without constant component.
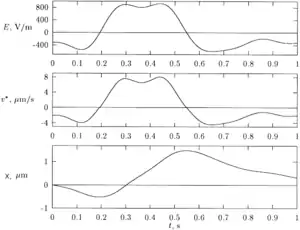
For the effect to show up, the dependence of friction/drag force on velocity must be nonlinear. This is the case for numerous substances known as non-Newtonian fluids. Among these are gels, and dilatant fluids, pseudoplastic fluids, liquid crystals. [5] Dedicated experiments[2] have determined for a standard DNA ladder up to 1500 bp long in 1.5% agarose gel. The dependence found, see Fig. 6, supports the possibility of nonlinear frictiophoresis in such a system. Based on data in Fig. 6, an optimal time course for driving electric field with zero mean, , has been found in,[2] which ensures maximal drift for 1500 b.p. long fragment, see Fig. 7.
The effect of unidirectional drift caused by periodic force with zero integral value has a peculiar dependence on the time course of the force applied. See the previous section for examples. This offers a new dimension to a set of separation problems.
DNA separation with respect to length
In the DNA fragments separation, zero mean periodic electric field is used in zero-integrated-field electrophoresis (ZIFE),[6] where the field time dependence similar to that shown in Fig. 3 is used. This allows to separate long fragments in agarose gel, nonseparable by standard constant field electrophoresis. The long DNA geometry and its manner of movement in a gel, known as reptation do not allow to apply directly the consideration based on Eq. (5), above.
Separation with respect to specific mass
It was observed, [7] that under certain physical conditions the mechanism described in Mathematical analysis section, above, can be used for separation with respect to specific mass, like particles made of isotopes of the same material.
Extensions
The idea of organizing directed drift with zero mean periodic drive have obtained further development for other configurations and other physical mechanism of nonlinearity.
Rotation by means of circular wave
An electric dipole rotating freely around -axis in a medium with nonlinear friction can be manipulated by applying electromagnetic wave polarized circularly along and composed of two harmonics. The equation of motion for this system is as follows:
where is the torque acting on the dipole due to circular wave:
where is the dipole moment component orthogonal to -axis and defines the dipole direction in the plane. By choosing proper phase shift in (6) it is possible to orient the dipole in any desired direction, . The direction is attained due to angular directed drift, which becomes zero when . [8] [9] A small detuning between the first and second harmonic in (6) results in continuous rotational drift.[9]
Modification of potential function
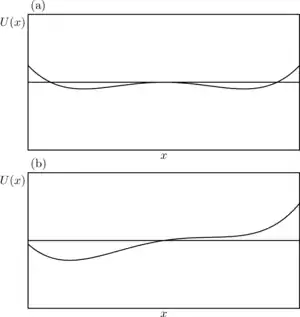
If a particle undergoes a directed drift while moving freely in accordance with Eq. (5), then it drifts similarly if a shallow enough potential field is imposed. Equation of motion in that case is:
where is the force due to potential field. The drift continues until a steep enough region in the course of is met, which is able to stop the drift. This kind of behavior, as rigorous mathematical analysis shows, [10] results in modification of by adding a linear in term. This may change the qualitatively, by, e.g. changing the number of equilibrium points, see Fig. 8. The effect may be essential during high frequency electric field acting on biopolymers. [11]
Another nonlinearity
For electrophoresis of colloid particles under a small strength electric field, the force in the right-hand side of Eq. (5) is linearly proportional to the strength of the electric field applied. For a high strength, the linearity is broken due to nonlinear polarization. As a result, the force may depend nonlinearly on the applied field:
In the last expression, even if the applied field, has zero mean, the applied force may happen to have a constant component that can cause a directed drift. [12] As above, for this to happen, must have more than a single sinusoidal harmonic. This same effect for a liquid in a tube may serve in electroosmotic pump driven with zero mean electric field.[13]
References
- Vidybida, Alexander; Serikov, Alexander (1985). "Electrophoresis by alternating fields in a non-Newtonian fluid". Physics Letters. 108 (3): 170–172. Bibcode:1985PhLA..108..170V. doi:10.1016/0375-9601(85)90853-9.
- Vidybida, A.K.; Erkızan, V.; Altungöz, O.; Çelebi, G. (2000). "Testing of nonlinear electrofrictiophoresis in agarose gel". Bioelectrochemistry. 92: 91–101. doi:10.1016/S0302-4598(00)00088-X.
- Function is antiperiodic if for some the following relation holds for all . Individual harmonics, like , are antiperiodic.
- Nordén, B.; Zolotaryuk, Y.; Christiansen, P.L.; Zolotaryuk, A.V. (2001). "Ratchet due to broken friction symmetry". Physical Review E. 65 (1): 011110. doi:10.1103/PhysRevE.65.011110. PMID 11800680. Nordén, B.; Zolotaryuk, Y.; Christiansen, P.L.; Zolotaryuk, A.V. (2002). "Ratchet device with broken friction symmetry". Applied Physics Letters. 80 (14): 2601–2603. Bibcode:2002ApPhL..80.2601N. doi:10.1063/1.1468900.
- Simoff, D.A.; Porter, R.S. (2011). "Rheology and Properties of Thermotropic Liquid Crystalline Poly (Bisphenol E Isophthalate-Co-Naphthalate)". Molecular Crystals and Liquid Crystals. 110 (1–4): 1–26. doi:10.1080/00268948408074493.
- Noolandi, J.; Turmel, C. (1995). "Preparation, manipulation, and pulse strategy for one-dimensional pulsed-field gel electrophoresis (ODPFGE)". Mol Biotechnol. 4 (1): 25–43. doi:10.1007/BF02907469. PMID 8521038.
-
Vidybida, A. "Unpublished observation". Cite journal requires
|journal=(help) - Andruschenko, A.P.; Vidybida, A.K. (1988). "Control of internal rotation in molecular-scale objects by alternating space-homogeneous electric field". Automation. 5: 58–61.
- Vidybida, A.K. (1999). "Ch.3 in:". Dynamical mechanisms of influence of alternating electromagnetic fields on macromolecular and cooperative systems (PDF) (Doktor thesis). Bogolyubov Institute for Theoretical Physics.
- Vidybida, A.K. (1987). "Modification of the Potential Function of a Mechanical System Caused by Periodic Action". Soviet Physics Doklady. 32: 113–115. Vidybida, A.K. (1987). "Modification of the Potential Function of a Mechanical System Caused by Periodic Action". Acta Mechanica. 67 (1–4): 183–190. doi:10.1007/BF01182131.
- Vidybida, A.K. (1989). "Periodic electric field as a biopolymer conformation switch: a possible mechanism". Eur Biophys J. 16 (6): 357–61. doi:10.1007/BF00257884. PMID 2924736. Vidybida, A.K. (1999). "Ch.2 in:". Dynamical mechanisms of influence of alternating electromagnetic fields on macromolecular and cooperative systems (PDF) (Doktor thesis). Bogolyubov Institute for Theoretical Physics.
- Dukhin, S.S.; Vidybida, A.K.; Dukhin, A.S.; Serikov, A.A. (1988). "Aperiodic Electrophoresis. Directed drift of dispersed particles in a uniform anharmonic alternating electric field". Kolloidnyi Zh. 49 (5): 752–755. Mishchuk, N.A.; Barinova, N.O. (2011). "Theoretical and experimental study of nonlinear electrophoresis". Colloid J. 73: 88–96. doi:10.1134/S1061933X11010133.
- US application 20050129526, "Method of using unbalanced alternating electric field in microfluidic devices", published 2005-06-16, assigned to DUKHIN ANDREI S. and DUKHIN STANISLAV