Parallel metaheuristic

An example of different implementations of the same PSO metaheuristic model.

In practice, optimization (and searching, and learning) problems are often NP-hard, complex, and time-consuming. Two major approaches are traditionally used to tackle these problems: exact methods and metaheuristics. Exact methods allow to find exact solutions but are often impractical as they are extremely time-consuming for real-world problems (large dimension, hardly constrained, multimodal, time-varying, epistatic problems). Conversely, metaheuristics provide sub-optimal (sometimes optimal) solutions in a reasonable time. Thus, metaheuristics usually allow to meet the resolution delays imposed in the industrial field as well as they allow to study general problem classes instead that particular problem instances. In general, many of the best performing techniques in precision and effort to solve complex and real-world problems are metaheuristics. Their fields of application range from combinatorial optimization, bioinformatics, and telecommunications to economics, software engineering, etc. These fields are full of many tasks needing fast solutions of high quality. See for more details on complex applications.

Metaheuristics fall in two categories: trajectory-based metaheuristics and population-based metaheuristics. The main difference of these two kind of methods relies in the number of tentative solutions used in each step of the (iterative) algorithm. A trajectory-based technique starts with a single initial solution and, at each step of the search, the current solution is replaced by another (often the best) solution found in its neighborhood. It is usual that trajectory-based metaheuristics allow to quickly find a locally optimal solution, and so they are called exploitation-oriented methods promoting intensification in the search space. On the other hand, population-based algorithms make use of a population of solutions. The initial population is in this case randomly generated (or created with a greedy algorithm), and then enhanced through an iterative process. At each generation of the process, the whole population (or a part of it) is replaced by newly generated individuals (often the best ones). These techniques are called exploration-oriented methods, since their main ability resides in the diversification in the search space.

Most basic metaheuristics are sequential. Although their utilization allows to significantly reduce the temporal complexity of the search process, this latter remains high for real-world problems arising in both academic and industrial domains. Therefore, parallelism comes as a natural way not to only reduce the search time, but also to improve the quality of the provided solutions.

For a comprehensive discussion on how parallelism can be mixed with metaheuristics see .

Metaheuristics for solving optimization problems could be viewed as walks through neighborhoods tracing search trajectories through the solution domains of the problem at hands:

Algorithm: Sequential trajectory-based general pseudo-code
    Generate(s(0));        // Initial solution
    t := 0;                // Numerical step
    while not Termination Criterion(s(t)) do
        s′(t) := SelectMove(s(t)); // Exploration of the neighborhood
        if AcceptMove(s′(t)) then
            s(t) := ApplyMove(s′(t));
            t := t + 1;
    endwhile

Walks are performed by iterative procedures that allow moving from one solution to another one in the solution space (see the above algorithm). This kind of metaheuristics perform the moves in the neighborhood of the current solution, i.e., they have a perturbative nature. The walks start from a solution randomly generated or obtained from another optimization algorithm. At each iteration, the current solution is replaced by another one selected from the set of its neighboring candidates. The search process is stopped when a given condition is satisfied (a maximum number of generation, find a solution with a target quality, stuck for a given time, . . . ).

A powerful way to achieve high computational efficiency with trajectory-based methods is the use of parallelism. Different parallel models have been proposed for trajectory-based metaheuristics, and three of them are commonly used in the literature: the parallel multi-start model, the parallel exploration and evaluation of the neighborhood (or parallel moves model), and the parallel evaluation of a single solution (or move acceleration model):

• Parallel multi-start model: It consists in simultaneously launching several trajectory-based methods for computing better and robust solutions. They may be heterogeneous or homogeneous, independent or cooperative, start from the same or different solution(s), and configured with the same or different parameters.
• Parallel moves model: It is a low-level master-slave model that does not alter the behavior of the heuristic. A sequential search would compute the same result but slower. At the beginning of each iteration, the master duplicates the current solution between distributed nodes. Each one separately manages their candidate/solution and the results are returned to the master.
• Move acceleration model: The quality of each move is evaluated in a parallel centralized way. That model is particularly interesting when the evaluation function can be itself parallelized as it is CPU time-consuming and/or I/O intensive. In that case, the function can be viewed as an aggregation of a certain number of partial functions that can be run in parallel.

Population-based metaheuristic are stochastic search techniques that have been successfully applied in many real and complex applications (epistatic, multimodal, multi-objective, and highly constrained problems). A population-based algorithm is an iterative technique that applies stochastic operators on a pool of individuals: the population (see the algorithm below). Every individual in the population is the encoded version of a tentative solution. An evaluation function associates a fitness value to every individual indicating its suitability to the problem. Iteratively, the probabilistic application of variation operators on selected individuals guides the population to tentative solutions of higher quality. The most well-known metaheuristic families based on the manipulation of a population of solutions are evolutionary algorithms (EAs), ant colony optimization (ACO), particle swarm optimization (PSO), scatter search (SS), differential evolution (DE), and estimation distribution algorithms (EDA).

Algorithm: Sequential population-based metaheuristic pseudo-code
    Generate(P(0)); // Initial population
    t := 0;          // Numerical step
    while not Termination Criterion(P(t)) do
        Evaluate(P(t)); // Evaluation of the population
        P′′(t) := Apply Variation Operators(P′(t)); // Generation of new solutions
        P(t + 1) := Replace(P(t), P′′(t)); // Building the next population
        t := t + 1;
    endwhile

For non-trivial problems, executing the reproductive cycle of a simple population-based method on long individuals and/or large populations usually requires high computational resources. In general, evaluating a fitness function for every individual is frequently the most costly operation of this algorithm. Consequently, a variety of algorithmic issues are being studied to design efficient techniques. These issues usually consist of defining new operators, hybrid algorithms, parallel models, and so on.

Parallelism arises naturally when dealing with populations, since each of the individuals belonging to it is an independent unit (at least according to the Pittsburg style, although there are other approaches like the Michigan one which do not consider the individual as independent units). Indeed, the performance of population-based algorithms is often improved when running in parallel. Two parallelizing strategies are specially focused on population-based algorithms:

1. Parallelization of computations, in which the operations commonly applied to each of the individuals are performed in parallel, and
2. Parallelization of population, in which the population is split in different parts that can be simply exchanged or evolved separately, and then joined later.

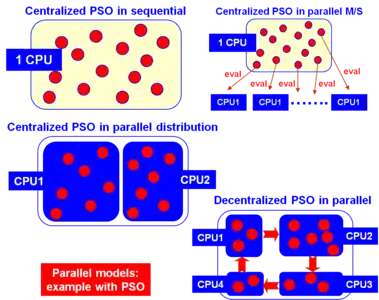
In the beginning of the parallelization history of these algorithms, the well-known master-slave (also known as global parallelization or farming) method was used. In this approach, a central processor performs the selection operations while the associated slave processors (workers) run the variation operator and the evaluation of the fitness function. This algorithm has the same behavior as the sequential one, although its computational efficiency is improved, especially for time-consuming objective functions. On the other hand, many researchers use a pool of processors to speed up the execution of a sequential algorithm, just because independent runs can be made more rapidly by using several processors than by using a single one. In this case, no interaction at all exists between the independent runs.

However, actually most parallel population-based techniques found in the literature utilize some kind of spatial disposition for the individuals, and then parallelize the resulting chunks in a pool of processors. Among the most widely known types of structured metaheuristics, the distributed (or coarse grain) and cellular (or fine grain) algorithms are very popular optimization procedures.

In the case of distributed ones, the population is partitioned in a set of subpopulations (islands) in which isolated serial algorithms are executed. Sparse exchanges of individuals are performed among these islands with the goal of introducing some diversity into the subpopulations, thus preventing search of getting stuck in local optima. In order to design a distributed metaheuristic, we must take several decisions. Among them, a chief decision is to determine the migration policy: topology (logical links between the islands), migration rate (number of individuals that undergo migration in every exchange), migration frequency (number of steps in every subpopulation between two successive exchanges), and the selection/replacement of the migrants.

In the case of a cellular method, the concept of neighborhood is introduced, so that an individual may only interact with its nearby neighbors in the breeding loop. The overlapped small neighborhood in the algorithm helps in exploring the search space because a slow diffusion of solutions through the population provides a kind of exploration, while exploitation takes place inside each neighborhood. See for more information on cellular Genetic Algorithms and related models.

Also, hybrid models are being proposed in which a two-level approach of parallelization is undertaken. In general, the higher level for parallelization is a coarse-grained implementation and the basic island performs a cellular, a master-slave method or even another distributed one.

• Cellular Evolutionary Algorithms
• Enrique Alba

• G. Luque, E. Alba, Parallel Genetic Algorithms. Theory and Real World Applications, Springer-Verlag, ISBN 978-3-642-22083-8, July 2011
• Alba E., Blum C., Isasi P., León C. Gómez J.A. (eds.), Optimization Techniques for Solving Complex Problems, Wiley, ISBN 978-0-470-29332-4, 2009
• E. Alba, B. Dorronsoro, Cellular Genetic Algorithms, Springer-Verlag, ISBN 978-0-387-77609-5, 2008
• N. Nedjah, E. Alba, L. de Macedo Mourelle, Parallel Evolutionary Computations, Springer-Verlag, ISBN 3-540-32837-8, 2006
• E. Alba, Parallel Metaheuristics: A New Class of Algorithms, Wiley, ISBN 0-471-67806-6, July 2005
• MALLBA
• JGDS
• DEME
• xxGA
• PSALHE-EA
• Paradiseo