Ring laser gyroscope

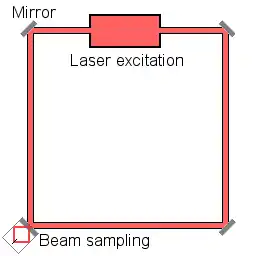
A ring laser gyroscope (RLG) consists of a ring laser having two independent counter-propagating resonant modes over the same path; the difference in the frequencies is used to detect rotation. It operates on the principle of the Sagnac effect which shifts the nulls of the internal standing wave pattern in response to angular rotation. Interference between the counter-propagating beams, observed externally, results in motion of the standing wave pattern, and thus indicates rotation.

For a somewhat similar system that uses fibre optic cables, see fibre optic gyroscope.
Ring laser gyroscope

Description

The first experimental ring laser gyroscope was demonstrated in the US by Macek and Davis in 1963.[1] Various organizations worldwide subsequently developed ring-laser technology further. Many tens of thousands of RLGs are operating in inertial navigation systems and have established high accuracy, with better than 0.01°/hour bias uncertainty, and mean time between failures in excess of 60,000 hours.

Schematic representation of a ring laser setup. At the beam sampling location, a fraction of each of the counterpropagating beams exits the laser cavity.

Ring laser gyroscopes can be used as the stable elements (for one degree of freedom each) in an inertial reference system. The advantage of using an RLG is that there are no moving parts (apart from the dither motor assembly, see further description below and laser-lock), compared to the conventional spinning gyroscope. This means there is no friction, which in turn eliminates a significant source of drift. Additionally, the entire unit is compact, lightweight and highly durable, making it suitable for use in mobile systems such as aircraft, missiles, and satellites. Unlike a mechanical gyroscope, the device does not resist changes to its orientation.

Contemporary applications of the Ring Laser Gyroscope (RLG) include an embedded GPS capability to further enhance accuracy of RLG Inertial Navigation Systems (INS)s on military aircraft, commercial airliners, ships and spacecraft. These hybrid INS/GPS units have replaced their mechanical counterparts in most applications. Where ultra accuracy is needed however, spin gyro based INSs are still in use today.[2]

Principle of operation

A certain rate of rotation induces a small difference between the time it takes light to traverse the ring in the two directions according to the Sagnac effect. This introduces a tiny separation between the frequencies of the counter-propagating beams, a motion of the standing wave pattern within the ring, and thus a beat pattern when those two beams are interfered outside the ring. Therefore, the net shift of that interference pattern follows the rotation of the unit in the plane of the ring.

RLGs, while more accurate than mechanical gyroscopes, suffer from an effect known as "lock-in" at very slow rotation rates. When the ring laser is hardly rotating, the frequencies of the counter-propagating laser modes become almost identical. In this case, crosstalk between the counter-propagating beams can allow for injection locking so that the standing wave "gets stuck" in a preferred phase, thus locking the frequency of each beam to that of the other, rather than responding to gradual rotation.

Forced dithering can largely overcome this problem. The ring laser cavity is rotated clockwise and anti-clockwise about its axis using a mechanical spring driven at its resonance frequency. This ensures that the angular velocity of the system is usually far from the lock-in threshold. Typical rates are 400 Hz, with a peak dither velocity of the order of 1 degree per second. Dither does not fix the lock-in problem completely, as each time the direction of rotation is reversed, a short time interval exists in which the rotation rate is near zero and lock-in can briefly occur. If a pure frequency oscillation is maintained, these small lock-in intervals can accumulate. This was remedied by introducing noise to the 400 Hz vibration.[3]

A different approach to avoiding lock-in is embodied in the Multioscillator Ring Laser Gyroscope,[4][5] wherein what is effectively two independent ring lasers (each having two counterpropagating beams) of opposite circular polarization coexist in the same ring resonator. The resonator incorporates polarization rotation (via a nonplanar geometry) which splits the fourfold-degenerate cavity mode (two directions, two polarizations each) into right- and left-circular-polarized modes separated by many hundreds of MHz, each having two counterpropagating beams. Nonreciprocal bias via the Faraday Effect, either in a special thin Faraday rotator or else via a longitudinal magnetic field on the gain medium, then further splits each circular polarization by typically a few hundred kHz, thus causing each ring laser to have a static output beat frequency of hundreds of kHz. One frequency increases and one decreases when inertial rotation is present, and the two frequencies are measured and then digitally subtracted to finally yield the net Sagnac-effect frequency splitting and thus determine the rotation rate. The Faraday bias frequency is chosen to be higher than any anticipated rotation-induced frequency difference, so the two counterpropagating waves have no opportunity to lock-in.

Fibre optic gyroscope

A related device is the fibre optic gyroscope which also operates on the basis of the Sagnac effect, but in which the ring is not a part of the laser. Rather, an external laser injects counter-propagating beams into an optical fiber ring, where rotation causes a relative phase shift between those beams when interfered after their pass through the fiber ring. The phase shift is proportional to the rate of rotation. This is less sensitive in a single traverse of the ring than the RLG, in which the externally observed phase shift is proportional to the accumulated rotation itself, not its derivative. However, the sensitivity of the fiber optic gyro is enhanced by having a long optical fiber, coiled for compactness, in which the Sagnac effect is multiplied according to the number of turns.

Example applications

See also

References
  1. Macek, W. M.; Davis, D. T. M. (1963). "Rotation rate sensing with traveling-wave ring lasers". Applied Physics Letters. AIP Publishing. 2 (3): 67–68. doi:10.1063/1.1753778. ISSN 0003-6951.
  2. Peter M. Taylor – INS Test Engineer Honeywell, Inc.
  3. Knowing Machines, Donald MacKenzie, The MIT Press, (1991).
  4. Statz, Hermann; Dorschner, T. A.; Holz, M.; Smith, I. W. (1985). "3. The multioscillator ring laser gyroscope". In Stich, M.L.; Bass, M. (eds.). Laser handbook. Elsevier (North-Holland Pub. Co). pp. 229-332. ISBN 0444869271.
  5. Volk, C. H. et al., Multioscillator Ring Laser Gyroscopes and their applications, in Optical Gyros and their Applications (NATO RTO-AG-339 AC/323(SCI)TP/9), Loukianov, D et al. (eds.) Retrieved 23 October 2019
  6. "Honeywell's ADIRU selected by Airbus". Farnborough. 22–28 July 2002. Archived from the original on 2006-10-17. Retrieved 2008-07-16.
  7. "Agni-III missile ready for induction". Press Trust of India. 2008-05-07. Retrieved 2008-05-08.
  8. "India successfully test fires Agni-IV missile". Economic Times India via Press Trust of India. 2014-01-20. Retrieved 2015-10-14.
  9. "Agni-V missile to take India into elite nuclear club". BBC News. 2012-04-19. Retrieved 2015-10-14.
  10. Digital Avionics Systems. IEEE, AIAA. 1995. ISBN 0-7803-3050-1. Retrieved 2008-10-16.
  11. "B-52 Maps Its Way Into New Century". fas.org. 19 Nov 1999. Retrieved 2009-02-24.
  12. "MK 39 MOD 3A Ring Laser" (PDF). Archived from the original (PDF) on 2009-02-05.
  13. Missile success – Frontline Magazine
  14. "Pakistan Aeronautical Complex Kamra – JF-17 Thunder Aircraft". www.pac.org.pk. Retrieved 2017-02-26.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.