Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid specified by either the cosine or sine functions with no phase angle that is plotted in polar coordinates. Rose curves or "rhodonea" were named by the Italian mathematician who studied them, Guido Grandi, between the years 1723 and 1728.[1]
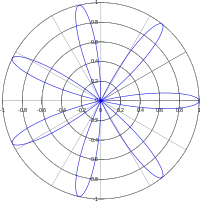

General overview
Specification
A rose is the set of points in polar coordinates specified by the polar equation
or in Cartesian coordinates using the parametric equations
- .
Roses can also be specified using the sine function.[3] Since
- .
Thus, the rose specified by is identical to that specified by rotated counter-clockwise by radians, which is one-quarter the period of either sinusoid.
Since they are specified using the cosine or sine function, roses are usually expressed as polar coordinate (rather than Cartesian coordinate) graphs of sinusoids that have angular frequency of and an amplitude of that determine the radial coordinate given the polar angle (though when is a rational number, a rose curve can be expressed in Cartesian coordinates since those can be specified as algebraic curves[4]).
General properties
Roses are directly related to the properties of the sinusoids that specify them.
- A rose specified as is symmetric about the polar axis because .
- A rose specified as is symmetric about the vertical line because .
- Graphs of roses are composed of petals. A petal is the shape formed by the graph of a half-cycle of the sinusoid that specifies the rose. (A cycle is a portion of a sinusoid that is one period long and consists of a positive half-cycle, the continuous set of points where and is long, and a negative half-cycle is the other half where .)
- The shape of each petal is same because the graphs of half-cycles have the same shape. The shape is given by the positive half-cycle with crest at specified by (that is bounded by the angle interval ). The petal is symmetric about the polar axis. All other petals are rotations of this petal about the pole, including those for roses specified by the sine function with same values for and .
- Consistent with the rules for plotting points in polar coordinates, a point in a negative half-cycle cannot be plotted at its polar angle because its radial coordinate is negative. The point is plotted by adding radians to the polar angle with a radial coordinate . Thus, positive and negative half-cycles can be coincident in the graph of a rose. In addition, roses are inscribed in the circle .
- When the period of the sinusoid is less than or equal to , the petal's shape is a single closed loop. A single loop is formed because the angle interval for a polar plot is and the angular width of the half-cycle is less than or equal to . When (or ) the plot of a half-cycle can be seen as spiraling out from the pole in more than one circuit around the pole until plotting reaches the inscribed circle where it spirals back to the pole, intersecting itself and forming one or more loops along the way. Consequently, each petal forms 2 loops when (or ), 3 loops when (or ), etc.
- A rose's petals will not intersect each other when the angular frequency is a non-zero integer; otherwise, petals intersect one another.
Roses with non-zero integer values of k
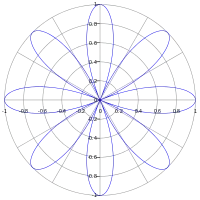
When is a non-zero integer, the curve will be rose-shaped with petals if is even, and petals when is odd.[5]
- The rose is inscribed in the circle , corresponding to the radial coordinate of all of its peaks.
- Because a polar coordinate plot is limited to polar angles between and , there are cycles displayed in the graph. No additional points need be plotted because the radial coordinate at is the same value at (which are crests for two different positive half-cycles for roses specified by the cosine function).
- When is even (and non-zero), each of the half-cycles is graphed. Each peak corresponds to a point lying on the circle . Line segments connecting successive peaks will form a regular polygon with an even number of vertices, and likewise, the roses are symmetric about the pole. The rose will be graphed in any continuous interval of polar angles radians long.
- When is odd, each of the positive half-cycles (or negative half-cycles) is graphed. Each peak corresponds to a point lying on the circle . Each of curve’s negative half-cycles is “hidden” in that they are coincident with a positive half-cycle that will be displayed. This means that in graphing these rose curves, only the positive half-cycles or only the negative half-cycles need to plotted in order to form the full curve. (Equivalently, a complete curve will be graphed by plotting any continuous interval of polar angles that is radians long such as to .[6]) Line segments connecting successive peaks will form a regular polygon with an odd number of vertices. The rose will be graphed in any continuous interval of polar angles radians long.
- The rose’s petals do not overlap.
A rose with is a circle with a diameter that lies on the polar axis when . The circle is the curve's single petal. (See the circle being formed at the end of the next section.)
A rose with is called a quadrifolium because it has 4 petals.
A rose with is called a trifolium[7] because it has 3 petals. The curve is also called the Paquerette de Mélibée.[8] (See the trifolium being formed at the end of the next section.)
Roses with rational number values for k
In general, when is a rational number in the form , where and are non-zero integers, the number of petals is the denominator of the expression .[9] This means that the number of petals is if both and are odd, and otherwise.[10]
- In the case when both and are odd, the positive and negative half-cycles of the sinusoid are coincident. In all other cases the positive and negative half-cycles are not coincident. Consequently, if graphing is started at , the full curve is completed at with petals whenever both and are odd, and with petals otherwise. In the latter case, the roses are symmetric about the pole, and the roses specified by the cosine and sine functions are coincident.
- The rose is inscribed in the circle , corresponding to the radial coordinate of all of its peaks.
- When , is a non-zero integer, and we have the case described in the section immediately above. (When is an integer, and , the number of petals is when is odd because and are odd, and when is even.)
- When each petal is a single closed loop; otherwise each petal has multiple loops because the period of the sinusoid has .
A rose with is called the Dürer folium, named after the German painter and engraver.[11] The roses specified by and are exactly the same even though .
A rose with is a limaçon trisectrix which has the angle trisection property. The rose has a single petal with two loops. (See the animation below.)
The rays displayed are the polar axis and .
Graphing starts at .



Roses with irrational number values for k
A rose curve specified with an irrational number for will never complete. Furthermore, the graph of the curve in this case forms a dense set (i.e., it comes arbitrarily close to every point in the unit disk).
Total and petal areas when k is a non-zero integer
The total area of a rose with polar equation of the form
- or
is
, when is even;
and
, when is odd.[12]
When is even, there are petals; and when is odd, there are petals, so the area of each petal is .
Offset parameter
Adding an offset parameter c to a sinusoid as the form
does not specify a rose but, rather, is the polar equation that specifies a limaçon.
See also
- Lissajous curve
- quadrifolium – a rose curve where k = 2.
- Maurer rose
- Rose (topology)
- Spirograph
Notes
- O'Connor, John J.; Robertson, Edmund F., "Rhodonea", MacTutor History of Mathematics archive, University of St Andrews.
- Mathematical Models by H. Martyn Cundy and A.P. Rollett, second edition, 1961 (Oxford University Press), p. 73.
- "Rose (Mathematics)". Retrieved 2021-02-02.
- Robert Ferreol. "Rose". Retrieved 2021-02-03.
- Eric W. weisstein. "Rose (Mathematics)". Wolfram MathWorld. Retrieved 2021-02-05.
- "Number of Petals of Odd Index Rhodonea Curve". ProofWiki.org. Retrieved 2021-02-03.
- "Trifolium". Retrieved 2021-02-02.
- Eric W. Weisstein. "Paquerette de Mélibée". Wolfram MathWorld. Retrieved 2021-02-05.
- Jan Wassenaar. "Rhodonea". Retrieved 2021-02-02.
- Robert Ferreol. "Rose". Retrieved 2021-02-05.
- Robert Ferreol. "Dürer Folium". Retrieved 2021-02-03.
- Robert Ferreol. "Rose". Retrieved 2021-02-03.
