Round-off error

A floating-point number system ${\displaystyle F}$ is characterized by ${\displaystyle 4}$ integers:

${\displaystyle \beta }$: base or radix

${\displaystyle p}$: precision

${\displaystyle [L,U]}$: exponent range, where ${\displaystyle L}$ is the lower bound and ${\displaystyle U}$ is the upper bound

• Any ${\displaystyle x\in F}$ has the following form:

${\displaystyle x=\pm (\underbrace {d_{0}.d_{1}d_{2}\ldots d_{p-1}} _{\text{mantissa}})_{\beta }\times \beta ^{\overbrace {E} ^{\text{exponent}}}=\pm d_{0}\times \beta ^{E}+d_{1}\times \beta ^{E-1}+\ldots +d_{p-1}\times \beta ^{E-(p-1)}}$

where ${\displaystyle d_{i}}$ is an integer such that ${\displaystyle 0\leq d_{i}\leq \beta -1}$ for ${\displaystyle i=0,1,\ldots ,p-1}$, and ${\displaystyle E}$ is an integer such that ${\displaystyle L\leq E\leq U}$.

• A floating-point number system is normalized if the leading digit ${\displaystyle d_{0}}$ is always nonzero unless the number is zero.[3] Since the mantissa is ${\displaystyle d_{0}.d_{1}d_{2}\ldots d_{p-1}}$, the mantissa of a nonzero number in a normalized system satisfies ${\displaystyle 1\leq {\text{ mantissa }}<\beta }$. Thus, the normalized form of a nonzero IEEE floating-point number is ${\displaystyle \pm 1.bb\ldots b\times 2^{E}}$ where ${\displaystyle b\in {0,1}}$. In binary, the leading digit is always ${\displaystyle 1}$ so it is not written out and is called the implicit bit. This gives an extra bit of precision so that the roundoff error caused by representation error is reduced.

• Since floating-point number system ${\displaystyle F}$ is finite and discrete, it cannot represent all real numbers which means infinite real numbers can only be approximated by some finite numbers through rounding rules. The floating-point approximation of a given real number ${\displaystyle x}$ by ${\displaystyle fl(x)}$ can be denoted.
  • The total number of normalized floating-point numbers is

${\displaystyle 2(\beta -1)\beta ^{p-1}(U-L+1)+1}$, where

${\displaystyle 2}$ counts choice of sign, being positive or negative

${\displaystyle (\beta -1)}$ counts choice of the leading digit

${\displaystyle \beta ^{p-1}}$ counts remaining mantissa

${\displaystyle U-L+1}$ counts choice of exponents

${\displaystyle 1}$ counts the case when the number is ${\displaystyle 0}$.

In the IEEE standard the base is binary, i.e. ${\displaystyle \beta =2}$, and normalization is used. The IEEE standard stores the sign, exponent, and mantissa in separate fields of a floating point word, each of which has a fixed width (number of bits). The two most commonly used levels of precision for floating-point numbers are single precision and double precision.

Suppose the usage of round-to-nearest and IEEE double precision.

• Example: the decimal number ${\displaystyle (9.4)_{10}=(1001.{\overline {0110}})_{2}}$ can be rearranged into

${\displaystyle +1.\underbrace {0010110011001100110011001100110011001100110011001100} _{\text{52 bits}}110\ldots \times 2^{3}}$

Since the ${\displaystyle 53^{rd}}$ bit to the right of the binary point is a ${\displaystyle 1}$ and is followed by other nonzero bits, the round-to-nearest rule requires rounding up, that is, add ${\displaystyle 1}$ bit to the ${\displaystyle 52^{nd}}$ bit. Thus, the normalized floating-point representation in IEEE standard of ${\displaystyle 9.4}$ is

${\displaystyle fl(9.4)=1.0010110011001100110011001100110011001100110011001101\times 2^{3}}$.

• Now the roundoff error can be calculated when representing ${\displaystyle 9.4}$ with ${\displaystyle fl(9.4)}$.

This representation is derived by discarding the infinite tail

${\displaystyle 0.{\overline {1100}}\times 2^{-52}\times 2^{3}=0.{\overline {0110}}\times 2^{-51}\times 2^{3}=0.4\times 2^{-48}}$

from the right tail and then added ${\displaystyle 1\times 2^{-52}\times 2^{3}=2^{-49}}$ in the rounding step.

Then ${\displaystyle fl(9.4)=9.4-0.4\times 2^{-48}+2^{-49}=9.4+(0.2)_{10}\times 2^{-49}}$.

Thus, the roundoff error is ${\displaystyle (0.2\times 2^{-49})_{10}}$.

The machine epsilon ${\displaystyle \epsilon _{mach}}$ can be used to measure the level of roundoff error when using the two rounding rules above. Below are the formulas and corresponding proof.[3] The first definition of machine epsilon is used here.

1. Round-by-chop: ${\displaystyle \epsilon _{mach}=\beta ^{1-p}}$
2. Round-to-nearest: ${\displaystyle \epsilon _{mach}={\frac {1}{2}}\beta ^{1-p}}$

Let ${\displaystyle x=d_{0}.d_{1}d_{2}\ldots d_{p-1}d_{p}\ldots \times \beta ^{n}\in \mathbb {R} }$ where ${\displaystyle n\in [L,U]}$, and let ${\displaystyle fl(x)}$ be the floating-point representation of ${\displaystyle x}$. Since round-by-chop is being used, it is ${\displaystyle {\begin{aligned}{\frac {|x-fl(x)|}{|x|}}&={\frac {|d_{0}.d_{1}d_{2}\ldots d_{p-1}d_{p}d_{p+1}\ldots \times \beta ^{n}-d_{0}.d_{1}d_{2}\ldots d_{p-1}\times \beta ^{n}|}{|d_{0}.d_{1}d_{2}\ldots \times \beta ^{n}|}}\\&={\frac {|d_{p}.d_{p+1}\ldots \times \beta ^{n-p}|}{|d_{0}.d_{1}d_{2}\ldots \times \beta ^{n}|}}\\&={\frac {|d_{p}.d_{p+1}d_{p+2}\ldots |}{|d_{0}.d_{1}d_{2}\ldots |}}\times \beta ^{-p}\end{aligned}}}$* In order to determine the maximum of this quantity, the is a need to find the maximum of the numerator and the minimum of the denominator. Since ${\displaystyle d_{0}\neq 0}$ (normalized system), the minimum value of the denominator is ${\displaystyle 1}$. The numerator is bounded above by ${\displaystyle (\beta -1).(\beta -1){\overline {(\beta -1)}}=\beta }$. Thus, ${\displaystyle {\frac {|x-fl(x)|}{|x|}}\leq {\frac {\beta }{1}}\times \beta ^{-p}=\beta ^{1-p}}$. Therefore, ${\displaystyle \epsilon =\beta ^{1-p}}$ for round-by-chop. The proof for round-to-nearest is similar.

• Note that the first definition of machine epsilon is not quite equivalent to the second definition when using the round-to-nearest rule but it is equivalent for round-by-chop.

Machine addition consists of lining up the decimal points of the two numbers to be added, adding them, and then storing the result again as a floating-point number. The addition itself can be done in higher precision but the result must be rounded back to the specified precision, which may lead to roundoff error.[3]

For example, adding ${\displaystyle 1}$ to ${\displaystyle 2^{-53}}$ in IEEE double precision as follows,

${\displaystyle {\begin{aligned}1.00\ldots 0\times 2^{0}+1.00\ldots 0\times 2^{-53}&=1.\underbrace {00\ldots 0} _{\text{52 bits}}\times 2^{0}+0.\underbrace {00\ldots 0} _{\text{52 bits}}1\times 2^{0}\\&=1.\underbrace {00\ldots 0} _{\text{52 bits}}1\times 2^{0}\end{aligned}}}$

• This is saved as ${\displaystyle 1.\underbrace {00\ldots 0} _{\text{52 bits}}\times 2^{0}}$ since round-to-nearest is used in IEEE standard. Therefore, ${\displaystyle 1+2^{-53}}$ is equal to ${\displaystyle 1}$ in IEEE double precision and the roundoff error is ${\displaystyle 2^{-53}}$.

From this example, it can be seen that roundoff error can be introduced when doing the addition of a large number and a small number because the shifting of decimal points in the mantissas to make the exponents match may cause the loss of some digits.

In general, the product of ${\displaystyle 2}$ ${\displaystyle p}$-digit mantissas contains up to ${\displaystyle 2p}$ digits, so the result might not fit in the mantissa.[3] Thus roundoff error will be involved in the result.

• For example, consider a normalized floating-point number system with the base ${\displaystyle \beta =10}$ and the mantissa digits are at most ${\displaystyle 2}$. Then ${\displaystyle fl(77)=7.7\times 10}$ and ${\displaystyle fl(88)=8.8\times 10}$. Note that ${\displaystyle 77\times 88=6776}$ but ${\displaystyle fl(6776)=6.7\times 10^{3}}$ since there at most ${\displaystyle 2}$ mantissa digits. The roundoff error would be ${\displaystyle 6776-fl(6776)=6776-6.7\times 10^{3}=76}$.

In general, the quotient of ${\displaystyle 2}$ ${\displaystyle p}$-digit mantissas may contain more than ${\displaystyle p}$-digits.[3] Thus roundoff error will be involved in the result.

• For example, if the normalized floating-point number system above is still being used, then ${\displaystyle 1/3=0.333\ldots }$ but ${\displaystyle fl(1/3)=fl(0.333\ldots )=3.3\times 10^{-1}}$. So, the tail ${\displaystyle 0.333\ldots -3.3\times 10^{-1}=0.00333\ldots }$ is cut off.

The subtracting of two nearly equal numbers is called subtractive cancellation.[3]

• When the leading digits are cancelled, the result may be too small to be represented exactly and it will just be represented as ${\displaystyle 0}$.
  • For example, let ${\displaystyle |\epsilon |<\epsilon _{mach}}$ and the second definition of machine epsilon is used here. What is the solution to ${\displaystyle (1+\epsilon )-(1-\epsilon )}$?
    It is known that ${\displaystyle 1+\epsilon }$ and ${\displaystyle 1-\epsilon }$ are nearly equal numbers, and ${\displaystyle (1+\epsilon )-(1-\epsilon )=1+\epsilon -1+\epsilon =2\epsilon }$. However, in the floating-point number system, ${\displaystyle fl((1+\epsilon )-(1-\epsilon ))=fl(1+\epsilon )-fl(1-\epsilon )=1-1=0}$. Although ${\displaystyle 2\epsilon }$ is easily big enough to be represented, both instances of ${\displaystyle \epsilon }$ have been rounded away giving ${\displaystyle 0}$.
• Even with a somewhat larger ${\displaystyle \epsilon }$, the result is still significantly unreliable in typical cases. There is not much faith in the accuracy of the value because the most uncertainty in any floating-point number is the digits on the far right.
  • For example, ${\displaystyle 1.99999\times 10^{2}-1.99998\times 10^{2}=0.00001\times 10^{2}=1\times 10^{-5}\times 10^{2}=1\times 10^{-3}}$. The result ${\displaystyle 1\times 10^{-3}}$ is clearly representable, but there is not much faith in it.

An algorithm or numerical process is called stable if small changes in the input only produce small changes in the output and it is called unstable if large changes in the output are produced.[11]

A sequence of calculations normally occur when running some algorithm. The amount of error in the result depends on the stability of the algorithm. Roundoff error will be magnified by unstable algorithms.

For example, ${\displaystyle y_{n}=\int _{0}^{1}\,{\frac {x^{n}}{x+5}}dx}$ for ${\displaystyle n=1,2,\ldots ,8}$ with ${\displaystyle y_{0}}$ given. It is easy to show that ${\displaystyle y_{n}={\frac {1}{n}}-5y_{n-1}}$. Suppose ${\displaystyle y_{0}}$ is our initial value and has a small representation error ${\displaystyle \epsilon }$, which means the initial input to this algorithm is ${\displaystyle y_{0}+\epsilon }$ instead of ${\displaystyle y_{0}}$. Then the algorithm does the following sequence of calculations.

${\displaystyle {\begin{aligned}y_{1}&=1-5(y_{0}+\epsilon )=1-5y_{0}-5\epsilon \\y_{2}&={\frac {1}{2}}-5(1-5y_{0}-5\epsilon )={\frac {1}{2}}-5+25y_{0}+5^{2}\epsilon \\\vdots \\y_{n}&=\ldots +5^{n}\epsilon \end{aligned}}}$

The roundoff error is amplified in succeeding calculations so this algorithm is unstable.

Comparison1

Comparison 2

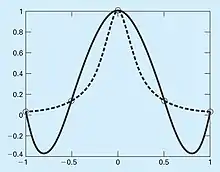
Even if a stable algorithm is used, the solution to a problem may still be inaccurate due to the accumulation of roundoff error when the problem itself is ill-conditioned.

The condition number of a problem is the ratio of the relative change in the solution to the relative change in the input.[3] A problem is well-conditioned if small relative changes in input result in small relative changes in the solution. Otherwise, the problem is ill-conditioned.[3] In other words, a problem is ill-conditioned if its condition number is "much larger" than ${\displaystyle 1}$.

The condition number is introduced as a measure of the roundoff errors that can result when solving ill-conditioned problems.[7]

For example, higher-order polynomials tend to be very ill-conditioned, that is, they tend to be highly sensitive to roundoff error.[7]

In 1901, Carl Runge published a study on the dangers of higher-order polynomial interpolation. He looked at the following simple-looking function:

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}}$

which is now called Runge's function. He took equidistantly spaced data points from this function over the interval ${\displaystyle [-1,1]}$. He then used interpolating polynomials of increasing order and found that as he took more points, the polynomials and the original curve differed considerably as illustrated in Figure “Comparison1” and Figure “Comparison 2”. Further, the situation deteriorated greatly as the order was increased. As shown in Figure “Comparison 2”, the fit has gotten even worse, particularly at the ends of the interval.

Click on the figures in order to see the full descriptions.

American Patriot missile

On 25 February 1991, during the Gulf War, an American Patriot missile battery in Dharan, Saudi Arabia, failed to intercept an incoming Iraqi Scud missile. The Scud struck an American Army barracks and killed 28 soldiers. A report of the then-General Accounting Office entitled "Patriot Missile Defense: Software Problem Led to System Failure at Dhahran, Saudi Arabia" reported on the cause of the failure: an inaccurate calculation of the time since boot due to computer arithmetic errors. Specifically, the time in tenths of a second, as measured by the system's internal clock, was multiplied by 10 to produce the time in seconds. This calculation was performed using a 24-bit fixed point register. In particular, the value 1/10, which has a non-terminating binary expansion, was chopped at 24 bits after the radix point. The small chopping error, when multiplied by the large number giving the time in tenths of a second, led to a significant error. Indeed, the Patriot battery had been up around 100 hours, and an easy calculation shows that the resulting time error due to the magnified chopping error was about 0.34 seconds. (The number 1/10 equals ${\displaystyle 1/2^{4}+1/2^{5}+1/2^{8}+1/2^{9}+1/2^{12}+1/2^{13}+\ldots }$. In other words, the binary expansion of 1/10 is ${\displaystyle 0.0001100110011001100110011001100\ldots }$. Now the 24 bit register in the Patriot stored instead ${\displaystyle 0.00011001100110011001100}$ introducing an error of ${\displaystyle 0.0000000000000000000000011001100\ldots }$ binary, or about ${\displaystyle 0.000000095}$ decimal. Multiplying by the number of tenths of a second in ${\displaystyle 100}$ hours gives ${\displaystyle 0.000000095\times 100\times 60\times 60\times 10=0.34}$). A Scud travels at about 1676 meters per second, and so travels more than half a kilometer in this time. This was far enough that the incoming Scud was outside the "range gate" that the Patriot tracked. Ironically, the fact that the bad time calculation had been improved in some parts of the code, but not all, contributed to the problem, since it meant that the inaccuracies did not cancel.[12]