Snub icosidodecadodecahedron

In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46. It has 104 faces (80 triangles, 12 pentagons, and 12 pentagrams), 180 edges, and 60 vertices.[1]

Snub icosidodecadodecahedron
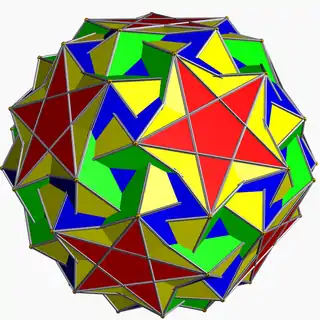TypeUniform star polyhedron
ElementsF = 104, E = 180
V = 60 (χ = −16)
Faces by sides(20+60){3}+12{5}+12{5/2}
Wythoff symbol| 5/3 3 5
Symmetry groupI, [5,3]+, 532
Index referencesU46, C58, W112
Dual polyhedronMedial hexagonal hexecontahedron
Vertex figure
3.3.3.5.3.5/3
Bowers acronymSided
3D model of a snub icosidodecadodecahedron

As the name indicates, it belongs to the family of snub polyhedra.

Cartesian coordinates

Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of

(±2α, ±2γ, ±2β),
(±(α+β/τ+γτ), ±(-ατ+β+γ/τ), ±(α/τ+βτ-γ)),
(±(-α/τ+βτ+γ), ±(-α+β/τ-γτ), ±(ατ+β-γ/τ)),
(±(-α/τ+βτ-γ), ±(α-β/τ-γτ), ±(ατ+β+γ/τ)) and
(±(α+β/τ-γτ), ±(ατ-β+γ/τ), ±(α/τ+βτ+γ)),

with an even number of plus signs, where

α = ρ+1 = ρ3,
β = τ2ρ2+τ2ρ+τ = τ2ρ4+τ,
γ = ρ2+τρ,

and where τ = (1+√5)/2 is the golden mean and ρ is the real solution to ρ3=ρ+1, or approximately 1.3247180. ρ is called the plastic constant. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one.

Medial hexagonal hexecontahedron
Medial hexagonal hexecontahedron
TypeStar polyhedron
Face
ElementsF = 60, E = 180
V = 104 (χ = −16)
Symmetry groupI, [5,3]+, 532
Index referencesDU46
dual polyhedronSnub icosidodecadodecahedron
3D model of a medial hexagonal hexecontahedron

The medial hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform snub icosidodecadodecahedron.

See also

References
  1. Maeder, Roman. "46: snub icosidodecadodecahedron". MathConsult.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.