Solid-state nuclear magnetic resonance

The resonance frequency of a nuclear spin depends on the strength of the magnetic field at the nucleus, which can be modified by the electron cloud or the proximity of another spin. In general, these local fields are orientation dependent. In media with no or little mobility (e.g. crystalline powders, glasses, large membrane vesicles, molecular aggregates), anisotropic local fields or interactions have substantial influence on the behaviour of nuclear spins. In contrast, in a classical liquid-state NMR experiment, Brownian motion averages anisotropic interactions to zero and they are therefore not reflected in the NMR spectrum.

Two directionally dependent interactions commonly found in solid-state NMR are the chemical shift anisotropy (CSA) induced by the electron cloud around the nucleus and the dipolar coupling to other nuclear spins. More such interactions exist, in particular the quadrupolar coupling of nuclei with spin quantum number >1/2 and dipolar couplings to electron spins. The anisotropic J-coupling is usually too small to be detected. The g-tensor is an anisotropic interaction in electron spin resonance. In mathematical terms, all these interactions can be described using the same formalism.

Anisotropic interactions modify the local fields and nuclear spin energy levels (and hence the resonance frequency) of nuclei in a molecule, and often contribute to line broadening in NMR spectra. Nevertheless, there is a range of situations when their presence either cannot be avoided, or is even particularly desired, as they encode structural parameters, such as orientation information, on chemical bonds of interest.

High-resolution conditions in solids (in a wider sense) can be established using magic angle spinning (MAS), macroscopic sample orientation, combinations of both of these techniques, and a variety of radio frequency (RF) irradiation patterns. While the latter allows decoupling of interactions in spin space, the others facilitate averaging of interactions in real space. In addition, line-broadening effects from microscopic inhomogeneities can be reduced by appropriate methods of sample preparation.

Under magic-angle spinning conditions, isotropic interactions can report on the local structure, e.g. by the isotropic chemical shift. In addition, decoupled interactions can be selectively re-introduced ("recoupling"), and used, for example, for controlled de-phasing or transfer of polarization to derive a number of structural parameters such as internuclear distances.

The residual line width (full width at half maximum) of ¹³C nuclei under MAS conditions at 5–15 kHz spinning frequency and strong ¹H decoupling by radio-frequency irradiation is typically on the order of 0.3–2 ppm. Even at MAS rates of 20 kHz and above, however, nonlinear groups of the same nuclei (i.e. not on a straight line) linked via homonuclear dipolar interactions can only be suppressed partially, leading to ¹H NMR line widths of 0.5 ppm and above, which is considerably more than in optimal solution state NMR conditions. Other interactions such as the quadrupolar interaction can lead to line widths of thousands of ppm due to the strength of the interaction. The first-order quadrupolar broadening is largely suppressed by sufficiently fast MAS, but the second-order quadrupolar broadening has a different angular dependence and cannot be removed by spinning at one angle alone. Ways to achieve line shapes without anisotropy-induced broadening for quadrupolar nuclei include spinning at two angles simultaneously (DOR, DOuble angle Rotation), sequentially (DAS), or through refocusing the second-order quadrupolar interaction with a two-dimensional experiment such as MQMAS or STMAS.

From the perspective of solution-state NMR, it can be desirable to limit motional averaging of dipolar interactions by alignment media. The resulting residual dipolar couplings (RDCs) are typically only a few Hz in magnitude, but do not destroy high-resolution conditions and provide a wealth of information, in particular on the orientation of molecular domains with respect to each other.

The dipolar coupling between two nuclei is inversely proportional to the cube of their distance. The fairly slow polarization transfer mediated by the dipolar interaction between two distant spins of the same kind, e.g. ¹³C, is dramatically slowed down by a strong coupling to a third such nucleus nearby. This usually undesirable effect is commonly referred to as dipolar truncation. It has been one of the major obstacles in efficient extraction of internuclear distances, which are crucial in the structural analysis of biomolecular structure. By means of isotope labeling schemes or radio-frequency pulse sequences, however, it has become possible to circumvent this problem in a number of ways. Another way of circumventing dipolar truncation is to study rare nuclei like ¹³C at their low natural isotopic abundance utilising DNP-assisted MAS NMR, where the probability of an interfering third spin nearby is almost 100 times lower.[2]

The chemical shielding is a local property of each nuclear site in a molecule or compound, and is proportional to the applied external magnetic field.

Specifically, the external magnetic field induces currents of the electrons in molecular orbitals. These induced currents create local magnetic fields that lead to characteristic changes in nuclear resonance frequency. These changes can be predicted from molecular structure using empirical rules or quantum-chemical calculations.

Under sufficiently fast magic angle spinning, or in solution-state NMR, the directionally dependent character of the chemical shielding is time-averaged to zero, leaving only the isotropic chemical shift.

The J-coupling or indirect nuclear spin-spin coupling (sometimes also called "scalar" coupling despite the fact that J is a tensor quantity) describes the interaction of nuclear spins through chemical bonds.

Vectors important for dipolar coupling

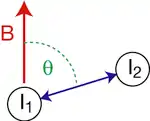
Nuclear spins exhibit a magnetic dipole moment, which generates a magnetic field that interacts with the dipole moments of other nuclei (dipolar coupling). The magnitude of the interaction is dependent on the spin species, the internuclear distance r, and the orientation, with respect to the external magnetic field B, of the vector connecting the two nuclear spins (see figure). The maximum dipolar coupling is given by the dipolar coupling constant d,

${\displaystyle d={\frac {\hbar \mu _{0}}{4\pi }}{\frac {\gamma _{1}\gamma _{2}}{r^{3}}}}$,

where γ₁ and γ₂ are the gyromagnetic ratios of the nuclei. In a strong magnetic field, the dipolar coupling depends on the angle θ between the internuclear vector and the external magnetic field B (see the figure) according to

${\displaystyle D\propto 3\cos ^{2}\theta -1}$.

D becomes zero for ${\displaystyle \theta =\arccos {\sqrt {1/3}}=\arctan {\sqrt {2}}}$ = 54.7°. Consequently, two nuclei with a dipolar coupling vector at an angle of θ_m = 54.7° to a strong external magnetic field have zero dipolar coupling. θ_m is called the magic angle. One technique for removing dipolar couplings, at least relatively weak ones, is magic angle spinning.

Nuclei with a spin quantum number >1/2 have a non-spherical charge distribution. This is known as a quadrupolar nucleus. A non spherical charge distribution can interact with an electric field gradient caused by some form of non-symmetry (e.g. in a trigonal bonding atom there are electrons around it in a plane, but not above or below it) to produce a change in the energy level in addition to the Zeeman effect. The quadrupolar interaction is the largest interaction in NMR apart from the Zeeman interaction, and they can even become comparable in size. The quadrupole coupling is so large that, unlike most other interactions, it cannot be treated to just the first order. This means you have a first and second order interaction, which can be treated separately. The first order interaction has an angular dependency with respect to the magnetic field of ${\displaystyle (3\cos ^{2}\theta -1)/2}$ (the P₂ Legendre polynomial), this means that spinning the sample around an axis making an angle of 54.7° with the external field averages out the first-order interaction over one rotation period (other local interactions, including chemical shift, paramagnetic coupling, and J-coupling, also have this angular dependency). However, the second-order quadrupolar interaction depends on the P₄ Legendre polynomial, which has zero points at 30.6° and 70.1°. These can be taken advantage of by either using DOR (DOuble angle Rotation) where you spin at two angles at the same time, or DAS (Double Angle Spinning) where you switch quickly between the two angles. Specialized hardware (probe) has been developed for such experiments. A revolutionary advance is Lucio Frydman's multiple quantum magic angle spinning (MQMAS) NMR in 1995 and it has become a routine method for obtaining high resolution solid-state NMR spectra of quadrupolar nuclei.[3][4] A similar method to MQMAS is satellite transisition magic angle spinning (STMAS) NMR proposed by Zhehong Gan in 2000.

Paramagnetic substances are subject to the Knight shift.

CP pulse sequence

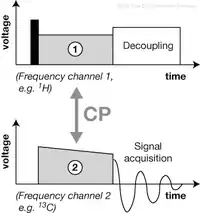
A fundamental RF pulse sequence and a building-block in many solid-state NMR experiments starts with cross-polarization (CP) (Pines, Gibby & Waugh 1973). It can be used to enhance the signal of nuclei with a low gyromagnetic ratio (e.g. ¹³C, ¹⁵N) by magnetization transfer from nuclei with a high gyromagnetic ratio (e.g. ¹H), or as a spectral editing method (e.g. directed ¹⁵N→¹³C CP in protein spectroscopy). To establish magnetization transfer, the RF pulses applied on the two frequency channels must fulfill the Hartmann–Hahn condition (Hartmann & Hahn 1962), that is, the nutation frequencies in both rf fields must be identical. Experimental optimization of this condition is one of the routine tasks in performing a (solid-state) NMR experiment.

CP is a basic building block of most pulse sequences in solid-state NMR spectroscopy. Given its importance, a pulse sequence employing direct excitation of ¹H spin polarization, followed by CP transfer to and signal detection of ¹³C, ¹⁵N or similar nuclei, is itself often referred to as CP experiment, or, in conjunction with MAS, as CP-MAS (Schaefer & Stejskal 1976) harv error: no target: CITEREFSchaeferStejskal1976 (help). It is the typical starting point of an investigation using solid-state NMR spectroscopy.

Spin interactions must be removed (decoupled) to increase the resolution of NMR spectra and isolate spin systems.

A technique that can substantially reduce or remove the chemical shift anisotropy and relatively weak dipolar couplings is sample rotation (most commonly magic angle spinning, but also off-magic angle spinning).

Heteronuclear decoupling by radio-frequency irradiation decouples spin interactions of the observed nuclei with other types of nuclei, primarily ¹H. Homonuclear decoupling by specially designed radio-frequency pulse sequences or fast MAS decouples spin interactions of nuclei that are the same as those being detected.

Although the broadened lines are often not desired, dipolar couplings between atoms in the crystal lattice can also provide very useful information. Dipolar coupling are distance dependent, and so they may be used to calculate interatomic distances in isotopically labeled molecules.

Because most dipolar interactions are averaged to zero by sample spinning, recoupling experiments with rotation-synchronized radio-frequency irradiation are needed to re-introduce desired dipolar couplings so they can be measured. A classical example of recoupling is the Rotational Echo DOuble Resonance (REDOR) experiment[5] which also can be the basis of an NMR crystallographic study.

In contrast to traditional approaches particular in protein NMR, in which the broad lines associated with protons effectively relegate this nucleus to mixing of magnetization, recent developments of hardware (very fast MAS) and reduction of dipolar interactions by deuteration have made protons as versatile as they are in solution NMR. This includes spectral dispersion in multi-dimensional experiments[6] as well as structurally valuable restraints and parameters important for studying the materials' dynamics.[7]

Studies of solids by NMR relaxation experiments are affected by the following general observations. The experimental decay of longitudinal magnetization follows the exponential law if the spin-diffusion mechanism is completely dominant; then a single relaxation time characterizes all of the nuclei, even those that are not chemically or structurally equivalent. The spin-diffusion mechanism is typical of systems with nuclei experiencing strong dipolar interactions (protons, fluorine or phosphorus nuclei at relatively small concentrations of paramagnetic centers) under relatively slow MAS. For other nuclei with weak dipolar coupling at a high concentration of paramagnetic centers, relaxation can be non-exponential following a stretched exponential function, exp(–(τ/T1)^β) or exp(–(τ/T2)^β). For paramagnetic solids, the β value of 0.5 corresponds to relaxation via direct electron–nucleus dipolar interactions without spin diffusion, while intermediate values between 0.5 and 1.0 can be attributed to a diffusion-limited mechanism.

Membrane proteins and amyloid fibrils, the latter related to Alzheimer's disease and Parkinson's disease, are two examples of applications where solid-state NMR spectroscopy complements solution-state NMR spectroscopy and beam diffraction methods (e.g. X-ray crystallography, electron microscopy). Solid-state NMR structure elucidation of proteins has traditionally been based on secondary chemical shifts and spatial contacts between heteronuclei. Currently, paramagnetic contact shifts[8] and specific proton-proton distances[9] are also used for higher resolution and longer-range distance restraints.

Solid-state NMR spectroscopy serves as an analysis tool in organic and inorganic chemistry, where it is used as a valuable tool to characterize chemical composition, supramolecular structure, local motions, kinetics, and thermodynamics, with the special ability to assign the observed behavior to specific sites in a molecule.

Objects of ssNMR studies in materials science are inorganic/organic aggregates in crystalline and amorphous states, composite materials, heterogeneous systems including liquid or gas components, suspensions, and molecular aggregates with dimensions on the nanoscale.

In many cases, NMR is the uniquely applicable method for measurement of porosity, particularly for porous systems containing partially filled pores or for dual-phase systems. ssNMR is one of the most effective technique for molecular-level investigation of interfaces.[10]

NMR can also be applied to art conservation. Different salts and moisture levels can be detected through the use of solid state NMR. However, sampling sizes retrieved from works of art in order to run through these large conducting magnets typically exceed levels deemed acceptable. Unilateral NMR techniques use portable magnets that are applied to the object of interest, bypassing the need for sampling. As such, unilateral NMR techniques prove to be useful in the art conservation world.[11]

• High Resolution Solid-State NMR of Quadrupolar Nuclei Grandinetti ENC Tutorial
• Laws David D., Hans- , Bitter Marcus L., Jerschow Alexej (2002). "Solid-State NMR Spectroscopic Methods in Chemistry". Angewandte Chemie International Edition. 41 (17): 3096–3129. doi:10.1002/1521-3773(20020902)41:17<3096::AID-ANIE3096>3.0.CO;2-X. PMID 12207374.CS1 maint: multiple names: authors list (link)
• Levitt, Malcolm H., Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley, Chichester, United Kingdom, 2001. (NMR basics, including solids)
• Duer, Melinda J., Introduction to Solid-State NMR Spectroscopy, Blackwell, Oxford, 2004. (Some detailed examples of ssNMR spectroscopy)

Books and major review articles

• McDermott, A, Structure and Dynamics of Membrane Proteins by Magic Angle Spinning Solid-State NMR Annual Review of Biophysics, v. 38, 2009.
• Mehring, M, Principles of High Resolution NMR in Solids, 2nd ed., Springer, Heidelberg, 1983.
• Slichter, C. P., Principles of Magnetic Resonance, 3rd ed., Springer, Heidelberg, 1990.
• Gerstein, B. C. and Dybowski, C., Transient Techniques in NMR of Solids, Academic Press, San Diego, 1985.
• Schmidt-Rohr, K. and Spiess, H.-W., Multidimensional Solid-State NMR and Polymers, Academic Press, San Diego, 1994.
• Dybowski, C. and Lichter, R. L., NMR Spectroscopy Techniques, Marcel Dekker, New York, 1987.
• Ramamoorthy, A., NMR Spectroscopy of Biological Solids, Taylor & Francis, New York, 2006.
• Bakhmutov, Vladimir. I. Solid-State NMR in Materials Science: Principles and Applications; CRC Press, 2012. Edition: 1st . ISBN 978-1439869635; ISBN 1439869634
• Bakhmutov, Vladimir. I. NMR Spectroscopy in Liquids and Solids. CRC Press, 2015. Edition: 1st . ISBN 978-1482262704, ISBN 1482262703.

References to books and research articles

• Andrew E. R.; Bradbury A.; Eades R. G. (1959). "Removal of Dipolar Broadening of Nuclear Magnetic Resonance Spectra of Solids by Specimen Rotation". Nature. 183 (4678): 1802–1803. Bibcode:1959Natur.183.1802A. doi:10.1038/1831802a0.
• Ernst, Bodenhausen, Wokaun: Principles of Nuclear Magnetic Resonance in One and Two Dimensions
• Hartmann, S.R.; Hahn, E.L. (1962). "Nuclear Double Resonance in the Rotating Frame". Phys. Rev. 128 (5): 2042–2053. Bibcode:1962PhRv..128.2042H. doi:10.1103/physrev.128.2042.
• Pines, A.; Gibby, M. G.; Waugh, J. S. (15 July 1973). "Proton‐enhanced NMR of dilute spins in solids" (PDF). The Journal of Chemical Physics. 59 (2): 569–590. doi:10.1063/1.1680061.
• Purcell, Torrey and Pound (1945).
• Schaefer J.; Stejskal E. O. (1976). "Carbon-13 Nuclear Magnetic Resonance of Polymers Spinning at the Magic Angle". Journal of the American Chemical Society. 98 (4): 1031–1032. doi:10.1021/ja00420a036.
• Gullion T.; Schaefer J. (1989). "Rotational-Echo, Double-Resonance NMR". J. Magn. Reson. 81: 196.
• MacKenzie, K.J.D and Smith, M.E. "Multinuclear Solid-State NMR of Inorganic Materials", Pergamon Materials Series Volume 6, Elsevier, Oxford 2002.