TFNP
In computational complexity theory, the complexity class TFNP is the class of total function problems which can be solved in nondeterministic polynomial time. That is, it is the class of function problems that are guaranteed to have an answer, and this answer can be checked in polynomial time, or equivalently it is the subset of FNP where a solution is guaranteed to exist. The abbreviation TFNP stands for "Total Function Nondeterministic Polynomial".
TFNP contains many natural problems that are of interest to computer scientists. These problems include integer factorization, finding a Nash Equilibrium of a game, and searching for local optima. TFNP is widely conjectured to contain problems that are computationally intractable, and several such problems have been shown to be hard under cryptographic assumptions.[1][2] However, there are no known unconditional intractability results or results showing NP-hardness of TFNP problems. TFNP is not believed to have any complete problems.[3]
Formal Definition
The class TFNP is formally defined as follows.
- A binary relation P(x,y) is in TFNP if and only if there is a deterministic polynomial time algorithm that can determine whether P(x,y) holds given both x and y, and for every x, there exists a y which is at most polynomially longer than x such that P(x,y) holds.
It was first defined by Megiddo and Papadimitriou in 1989,[4] although TFNP problems and subclasses of TFNP had been defined and studied earlier.[5]
Connections to Other Complexity Classes
F(NP coNP)
The complexity class F(NP coNP) can be defined in two different ways, and those ways are not known to be equivalent. One way applies F to the machine model for NP coNP. It is known that with this definition, F(NP coNP) coincides with TFNP.[6] To see this, first notice that the inclusion TFNP ⊆ F(NP coNP) follows easily from the definitions of the classes. All "yes" answers to problems in TFNP can be easily verified by definition, and since problems in TFNP are total, there are no "no" answers, so it is vacuously true that "no" answers can be easily verified. For the reverse inclusion, let R be a binary relation in F(NP coNP). Decompose R into R1 R2 such that (x, 0y) ∈ R1 precisely when (x, y) ∈ R and y is a "yes" answer, and let R2 be (x, 1y) such (x, y) ∈ R and y is a "no" answer. Then the binary relation R1 ∪ R2 is in TFNP.
The other definition uses that NP coNP is known to be a well-behaved class of decision problems, and applies F to that class. With this definition, if NP coNP = P then F(NP coNP) = FP.
Connection to NP
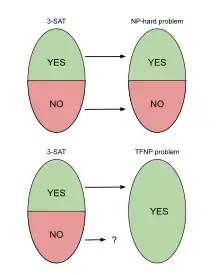
NP is one of the most widely studied complexity classes. The conjecture that there are intractable problems in NP is widely accepted and often used as the most basic hardness assumption. Therefore, it is only natural to ask how TFNP is related to NP. It is not difficult to see that solutions to problems in NP can imply solutions to problems in TFNP. However, there are no TFNP problems which are known to be NP-hard. Intuition for this fact comes from the fact that problems in TFNP are total. For a problem to be NP-hard, there must exist a reduction from some NP-complete problem to the problem of interest. A typical reduction from problem A to problem B is performed by creating and analyzing a map that sends "yes" instances of A to "yes" instances of B and "no" instances of A to "no" instances of B. However, TFNP problems are total, so there are no "no" instances for this type of reduction, causing common techniques to be difficult to apply. Beyond this rough intuition, there are several concrete results that suggest that it might be difficult or even impossible to prove NP-hardness for TFNP problems. For example, if any TFNP problem is NP-complete, then NP = coNP,[7] which is generally conjectured to be false, but is still a major open problem in complexity theory. This lack of connections with NP is a major motivation behind the study of TFNP as its own independent class.
Notable Subclasses
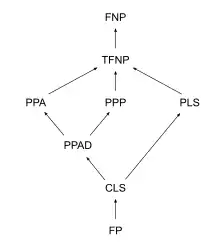
The structure of TFNP is often studied through the study of its subclasses. These subclasses are defined by the mathematical theorem by which solutions to the problems are guaranteed. One appeal of studying subclasses of TFNP is that although TFNP is believed not to have any complete problems, these subclasses are defined by a certain complete problem, making them easier to reason about.
PLS
PLS (standing for "Polynomial Local Search") is a class of problems designed to model the process of searching for a local optimum for a function. In particular, it is the class of total function problems that are polynomial-time reducible to the following problem
- Given input circuits A and B each with n input and output bits, find x such that A(B(x)) ≤ A(X).
It contains the class CLS.
PPA
PPA (standing for "Polynomial time Parity Argument") is the class of problems whose solution is guaranteed by the handshaking lemma: any undirected graph with an odd degree vertex must have another odd degree vertex. It contains the subclasses PWPP and PPAD.
PPP
PPP (standing for "Polynomial time Pigeonhole Principle") is the class of problems whose solution is guaranteed by the Pigeonhole principle. More precisely, it is the class of problems that can be reduced in polynomial time to the Pigeon problem, defined as follows
- Given circuit C with n input and output bits, find x such that C(x) = 0 or x ≠ y such that C(x) = C(y).
PPP contains the classes PPAD and PWPP. Notable problems in this class include the short integer solution problem.[8]
PPAD
PPAD (standing for "Polynomial time Parity Argument, Directed") is a restriction of PPA to problems whose solutions are guaranteed by a directed version of the handshake lemma. It is often defined as the set of problems that are polynomial-time reducible to End-of-a-Line:
- Given circuits S and P with n input and output bits S(0) ≠ 0 and P(0) = 0, find x such that P(S(x)) ≠ x or x ≠ 0 such that S(P(x)) ≠ x.
PPAD is in the intersection of PPA and PPP, and it contains CLS.
CLS
CLS (standing for "Continuous Local Search") is a class of search problems designed to model the process of finding a local optima of a continuous function over a continuous domain. It is defined as the class of problems that are polynomial-time reducible to the Continuous Localpoint problem:
- Given two Lipschitz continuous functions f and p and parameters ε and λ, find an ε-approximate fixed point of f with respect to p or two points that violate the λ-continuity of p or f.
This class was first defined by Daskalakis and Papadimitriou in 2011.[9] It is contained in the intersection of PPAD and PLS, and was designed to be a class of relatively simple optimization problems that still contains many interesting problems that are believed to be hard.
FP
FP (complexity) (standing for "Function Polynomial") is the class of function problems that can be solved in deterministic polynomial time. FP CLS, and it is conjectured that this inclusion is strict. This class represents the class of function problems that are believed to be computationally tractable (without randomization). If TFNP = FP, then P = NP ∩ coNP, which should be intuitive given the fact that TFNP = F(NP coNP). However, it is generally conjectured that P ≠ NP ∩ coNP, and so TFNP ≠ FP.
References
- Garg, Pandey, and Srinivasan. Revisiting Cryptographic Hardness of Finding a Nash Equilibrium. CRYPTO 2016.
- Habàcek and Yogev. Hardness of Continuous Local Search: Query Complexity and Cryptographic Lower Bounds. SODA 2016.
- Goldberg and Papadimitriou. Towards a Unified Complexity Theory of Total Functions. 2018.
- Megiddo and Papadimitriou. A Note on Total Functions, Existence Theorems and Computational Complexity. Theoretical Computer Science 1989.
- Johnson, Papadimitriou, and Yannakakis. How Easy is Local Search?. Journal of Computer System Sciences, 1988.
- Megiddo and Papadimitriou. A Note on Total Functions, Existence Theorems and Computational Complexity. Theoretical Computer Science 1989.
- Goldberg and Papadimitriou. Towards a Unified Complexity Theory of Total Functions. 2018.
- Sotiraki, Zampetakis, and Zidelis. PPP-Completeness with Connections to Cryptography. FOCS 2018
- Daskalakis and Papadimitriou. Continuous Local Search. SODA 2011.
