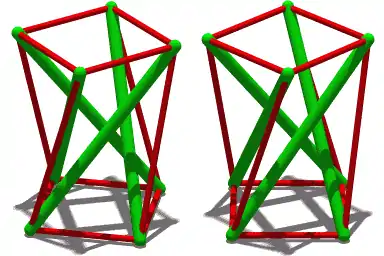
Tensegrity

Tensegrity, tensional integrity or floating compression is a structural principle based on a system of isolated components under compression inside a network of continuous tension, and arranged in such a way that the compressed members (usually bars or struts) do not touch each other while the prestressed tensioned members (usually cables or tendons) delineate the system spatially.[1]

For the movement system created by Carlos Castaneda, see Tensegrity (Castaneda).

The simplest tensegrity structure (a T3-prism). Each of three compression members (green) is symmetric with the other two, and symmetric from end to end. Each end is connected to three cables (red), which provide tension and precisely define the position of that end in the same way as the three cables in the Skylon define the bottom end of its tapered pillar.
Stereo image
Left frame 
Animation A similar structure but with four compression members.

The term was coined by Buckminster Fuller in the 1960s as a portmanteau of "tensional integrity".[2] The other denomination of tensegrity, floating compression, was used mainly by the constructivist artist Kenneth Snelson.

Concept

Tensegrity structures are based on the combination of a few simple design patterns:

  • members loaded in either pure compression or pure tension, which means that the structure will only fail if the cables yield or the rods buckle. This enables the material properties and cross-sectional geometry of each member to be optimized to the particular load it carries.
  • preload or tensional prestress allows cables to always be in tension, to maintain structural integrity.
  • mechanical stability, which allows the members to remain in tension/compression as stress on the structure increases. The structure also becomes stiffer as cable tension increases.

Because of these patterns, no structural member experiences a bending moment and there are no shear stresses within the system. This can produce exceptionally strong and rigid structures for their mass and for the cross section of the components. The loading of at least some tensegrity structures causes an auxetic response and negative Poisson ratio, e.g. the T3-prism and 6-strut tensegrity icosahedron.

The Skylon at the Festival of Britain, 1951

A conceptual building block of tensegrity is seen in the 1951 Skylon. Six cables, three at each end, hold the tower in position. The three cables connected to the bottom "define" its location. The other three cables are simply keeping it vertical.

A three-rod tensegrity structure (shown to the right) builds on this simpler structure: the ends of each green rod look like the top and bottom of the Skylon. As long as the angle between any two cables is smaller than 180°, the position of the rod is well defined. While three cables are the minimum required for stability, additional cables can be attached to each node for aesthetic purposes or to build in additional stability. For example, Snelson's Needle Tower uses a repeated pattern built using nodes that are connected to 5 cables each.

Eleanor Heartney points out visual transparency as an important aesthetic quality of these structures.[3] Korkmaz et al.[4][5] has argued that lightweight tensegrity structures are suitable for adaptive architecture.

Applications

Tensegrities saw increased application in architecture beginning in the 1960s, when Maciej Gintowt and Maciej Krasiński designed Spodek arena complex (in Katowice, Poland), as one of the first major structures to employ the principle of tensegrity. The roof uses an inclined surface held in check by a system of cables holding up its circumference. Tensegrity principles were also used in David Geiger's Seoul Olympic Gymnastics Arena (for the 1988 Summer Olympics), and the Georgia Dome (for the 1996 Summer Olympics). Tropicana Field, home of the Tampa Bay Rays major league baseball team, also has a dome roof supported by a large tensegrity structure.

Largest tensegrity bridge in the world, Kurilpa Bridge – Brisbane

On 4 October 2009, the Kurilpa Bridge opened across the Brisbane River in Queensland, Australia. A multiple-mast, cable-stay structure based on the principles of tensegrity, it is currently the world's largest tensegrity bridge.

A 12m high tensegrity structure exhibit at the Science City, Kolkata.

Since the early 2000s, tensegrities have also attracted the interest of roboticists due to their potential to design lightweight and resilient robots. Numerous researches have investigated tensegrity rovers, bio-mimicking robots, and modular soft robots. The most famous tensegrity robot is the Super Ball,[6] a rover for space exploration currently under developments at NASA Ames.

Biology

Biotensegrity, a term coined by Dr. Stephen Levin, is the application of tensegrity principles to biological structures.[7] Biological structures such as muscles, bones, fascia, ligaments and tendons, or rigid and elastic cell membranes, are made strong by the unison of tensioned and compressed parts. The musculoskeletal system maintains tension in a continuous network of muscles and connective tissues,[8] while the bones provide discontinuous compressive support. Even the human spine, which seems at first glance like a stack of vertebrae resting on each other, is actually a tensegrity structure.[9]

Donald E. Ingber has developed a theory of tensegrity to describe numerous phenomena observed in molecular biology.[10] For instance, the expressed shapes of cells, whether it be their reactions to applied pressure, interactions with substrates, etc., all can be mathematically modeled by representing the cell's cytoskeleton as a tensegrity. Furthermore, geometric patterns found throughout nature (the helix of DNA, the geodesic dome of a volvox, Buckminsterfullerene, and more) may also be understood based on applying the principles of tensegrity to the spontaneous self-assembly of compounds, proteins,[11] and even organs. This view is supported by how the tension-compression interactions of tensegrity minimize material needed to maintain stability and achieve structural resiliency.[12] Therefore, natural selection pressures would likely favor biological systems organized in a tensegrity manner.

As Ingber explains: quote|The tension-bearing members in these structures – whether Fuller's domes or Snelson's sculptures – map out the shortest paths between adjacent members (and are therefore, by definition, arranged geodesically). Tensional forces naturally transmit themselves over the shortest distance between two points, so the members of a tensegrity structure are precisely positioned to best withstand stress. For this reason, tensegrity structures offer a maximum amount of strength.[10]

In embryology, Richard Gordon proposed that Embryonic differentiation waves are propagated by an 'organelle of differentiation'[13] where the cytoskeleton is assembled in a bistable tensegrity structure at the apical end of cells called the 'cell state splitter'.[14]

History
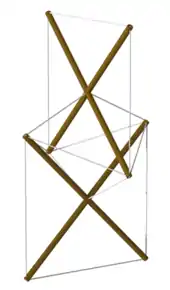
Kenneth Snelson's 1948 X-Module Design as embodied in a two-module column[15]

The origins of tensegrity are controversial.[16] Many traditional structures, such as skin-on-frame kayaks and shōji, use tension and compression elements in a similar fashion.

In 1948, artist Kenneth Snelson produced his innovative "X-Piece" after artistic explorations at Black Mountain College (where Buckminster Fuller was lecturing) and elsewhere. Some years later, the term "tensegrity" was coined by Fuller, who is best known for his geodesic domes. Throughout his career, Fuller had experimented with incorporating tensile components in his work, such as in the framing of his dymaxion houses.[17]

Snelson's 1948 innovation spurred Fuller to immediately commission a mast from Snelson. In 1949, Fuller developed a tensegrity-icosahedron based on the technology, and he and his students quickly developed further structures and applied the technology to building domes. After a hiatus, Snelson also went on to produce a plethora of sculptures based on tensegrity concepts. His main body of work began in 1959 when a pivotal exhibition at the Museum of Modern Art took place. At the MOMA exhibition, Fuller had shown the mast and some of his other work.[18] At this exhibition, Snelson, after a discussion with Fuller and the exhibition organizers regarding credit for the mast, also displayed some work in a vitrine.[19]

Snelson's best known piece is his 18-meter-high Needle Tower of 1968.

Russian artist Viatcheslav Koleichuk claimed that the idea of tensegrity was invented first by Kārlis Johansons (lv), a Soviet avant-garde artist of Latvian descent, who contributed some works to the main exhibition of Russian constructivism in 1921.[20] Koleichuk's claim was backed up by Maria Gough for one of the works at the 1921 constructivist exhibition.[21] Snelson has acknowledged the constructivists as an influence for his work (query?).[22] French engineer David Georges Emmerich has also noted how Kārlis Johansons's work (and industrial design ideas) seemed to foresee tensegrity concepts.[23]

Stability

Tensegrity prisms

The three-rod tensegrity structure (3-way prism) has the property that, for a given (common) length of compression member “rod” (there are three total) and a given (common) length of tension cable “tendon” (six total) connecting the rod ends together, there is a particular value for the (common) length of the tendon connecting the rod tops with the neighboring rod bottoms that causes the structure to hold a stable shape. For such a structure, it is straightforward to prove that the triangle formed by the rod tops and that formed by the rod bottoms are rotated with respect to each other by an angle of 5π/6 (radians).[24]

The stability (“prestressability”) of several 2-stage tensegrity structures are analyzed by Sultan, et al.[25]

Tensegrity icosahedra
Mathematical model of the tensegrity icosahedron
Different shapes of tensegrity icosahedra, depending on the ratio between the lengths of the tendons and the struts.

The polyhedron which corresponds directly to the geometry of the tensegrity icosahedron is called the Jessen's icosahedron. Its spherical dynamics were of special interest to Buckminster Fuller,[26] who referred to its expansion-contraction transformations around a stable equilibrium as jitterbug motion.[27]

The following is a mathematical model for figures related to the tensegrity icosahedron, explaining why it is a stable construction, albeit with infinitesimal mobility.[28]

Consider a cube of side length 2d, centered at the origin. Place a strut of length 2l in the plane of each cube face, such that each strut is parallel to one edge of the face and is centered on the face. Moreover, each strut should be parallel to the strut on the opposite face of the cube, but orthogonal to all other struts. If the Cartesian coordinates of one strut are and , those of its parallel strut will be, respectively, and . The coordinates of the other strut ends (vertices) are obtained by permuting the coordinates, e.g., (rotational symmetry in the main diagonal of the cube).

The distance s between any two neighboring vertices (0, d, l) and (d, l, 0) is

Imagine this figure built from struts of given length 2l and tendons (connecting neighboring vertices) of given length s, with . The relation tells us there are two possible values for d: one realized by pushing the struts together, the other by pulling them apart. For example, for the minimal figure (d = 0) is a regular octahedron and the maximal figure (d = l) is a quasiregular cubeoctahedron. In the case we have s = 2d, so the convex hull of the golden ratio figure () is a regular icosahedron. Since no article on the kinematics of polytopes would be complete without a Coxeter reference, it is appropriate to note here that by 1940 (prior to Jessen's icosahedron or the discovery of the tensegrity icosahedron) Coxeter had already shown how the twelve vertices of the icosahedron can be obtained by dividing the twelve edges of an octahedron according to the golden ratio, as one of the continuous series of (generally irregular) icosahedra with faces consisting of eight equilateral triangles and twelve isosceles triangles, ranging from cuboctahedron to octahedron (as limit cases), that can be produced by such a process of division.[29]

In the particular case the two extremes coincide, and , therefore the figure is the stable tensegrity icosahedron.

Since the tensegrity icosahedron represents an extremal point of the above relation, it has infinitesimal mobility: a small change in the length s of the tendon (e.g. by stretching the tendons) results in a much larger change of the distance 2d of the struts.

Patents
  • U.S. Patent 3,063,521, "Tensile-Integrity Structures," 13 November 1962, Buckminster Fuller.
  • French Patent No. 1,377,290, "Construction de Reseaux Autotendants", 28 September 1964, David Georges Emmerich.
  • French Patent No. 1,377,291, "Structures Linéaires Autotendants", 28 September 1964, David Georges Emmerich.
  • U.S. Patent 3,139,957, "Suspension Building" (also called aspension), 7 July 1964, Buckminster Fuller.
  • U.S. Patent 3,169,611, "Continuous Tension, Discontinuous Compression Structure," 16 February 1965, Kenneth Snelson.
  • U.S. Patent 3,866,366, "Non-symmetrical Tension-Integrity Structures," 18 February 1975, Buckminster Fuller.

Basic tensegrity structures
  • The simplest tensegrity structure, a 3-prism
  • Another 3-prism
  • A similar structure but with four compression members
  • Proto-Tensegrity Prism by Karl Ioganson, 1921[gallery 1]
  • Tensegrity Icosahedron, Buckminster Fuller, 1949[gallery 2]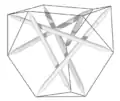
  • Tensegrity Tetrahedron, Francesco della Salla, 1952[gallery 3]
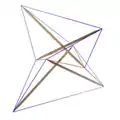  • Tensegrity X-Module Tetrahedron, Kenneth Snelson, 1959[gallery 4]
  • Kenneth Snelson's Needle Tower art sculpture.
  • Dissipate, an hourglass tower art sculpture including tensegrity structure, constructed at AfrikaBurn, 2015, a Burning Man regional event
  • The NASA SUPERball Tensegrity Robot is an early prototype to land on another planet without an airbag, and then be mobile to explore. The tensegrity structure provides structural compliance absorbing landing impact forces and motion is applied by changing cable lengths, 2014.
  • A tensegrity dome made of garden stakes and nylon twine built in the yard of a house, 2009

See also

Notes
  1. Gómez-Jáuregui 2010, p. 28. Fig. 2.1
  2. Fuller & Marks 1960, Fig. 270.
  3. Fuller & Marks 1960, Fig. 268.
  4. Lalvani 1996, p. 47

References
  1. Gómez-Jáuregui, V (2010). Tensegrity Structures and their Application to Architecture. Servicio de Publicaciones Universidad de Cantabria. p. 19. ISBN 978-8481025750.
  2. Swanson, RL (2013). "Biotensegrity: a unifying theory of biological architecture with applications to osteopathic practice, education, and research-a review and analysis". The Journal of the American Osteopathic Association. 113 (1): 34–52. doi:10.7556/jaoa.2013.113.1.34. PMID 23329804.
  3. Eleanor Hartley, "Ken Snelson and the Aesthetics of Structure," in the Marlborough Gallery catalogue for Kenneth Snelson: Selected Work: 1948–2009, exhibited 19 February through 21 March 2009.
  4. Korkmaz, et al. (June 2011)
  5. Korkmaz, Bel Hadj Ali & Smith 2011
  6. Hall, Loura (2 April 2015). "Super Ball Bot". NASA. Retrieved 18 June 2020.
  7. Levin, Stephen (2015). "16. Tensegrity, The New Biomechanics". In Hutson, Michael; Ward, Adam (eds.). Oxford Textbook of Musculoskeletal Medicine. Oxford University Press. pp. 155–56, 158–60. ISBN 978-0-19-967410-7.
  8. Souza et al. 2009
  9. Levin, Stephen M. (1 September 2002). "The tensegrity-truss as a model for spine mechanics: biotensegrity". Journal of Mechanics in Medicine and Biology. 02 (3n04): 375–88. doi:10.1142/S0219519402000472. ISSN 0219-5194.
  10. Ingber, Donald E. (January 1998). "The Architecture of Life" (PDF). Scientific American. 278 (1): 48–57. doi:10.1038/scientificamerican0198-48. PMID 11536845. Archived from the original (PDF) on 15 May 2005.
  11. Edwards, Scott A.; Wagner, Johannes; Gräter, Frauke (2012). "Dynamic Prestress in a Globular Protein". PLOS Computational Biology. 8 (5): e1002509. Bibcode:2012PLSCB...8E2509E. doi:10.1371/journal.pcbi.1002509. PMC 3349725. PMID 22589712.
  12. Skelton, Robert (2016). "Globally stable minimal mass compressive tensegrity structures". Composite Structures. 141: 346–54. doi:10.1016/j.compstruct.2016.01.105.
  13. Gordon, N.K. and Gordon, R. The organelle of differentiation in embryos: the cell state splitter [invited review]. Theor. Biol. Med. Model. 13(Special issue: Biophysical Models of Cell Behavior, Guest Editor: Jack A. Tuszynski), #11. 2016
  14. Gordon, Richard (1999). The Hierarchical Genome and Differentiation Waves. Series in Mathematical Biology and Medicine. 3. doi:10.1142/2755. ISBN 978-981-02-2268-0.
  15. Gough, Maria (Spring 1998). "In the Laboratory of Constructivism: Karl Ioganson's Cold Structures". October. 84: 90–117 [109]. doi:10.2307/779210. JSTOR 779210.
  16. Gómez-Jáuregui, V. (2009). "Controversial Origins of Tensegrity" (PDF). International Association of Spatial Structures IASS Symposium 2009, Valencia.
  17. Fuller & Marks 1960, Ch. Tensegrity
  18. See photo of Fuller's work at this exhibition in his 1961 article on tensegrity for the Portfolio and Art News Annual (No. 4).
  19. Lalvani 1996, p. 47
  20. Droitcour, Brian (18 August 2006). "Building Blocks". The Moscow Times. Archived from the original on 7 October 2008. Retrieved 28 March 2011. With an unusual mix of art and science, Vyacheslav Koleichuk resurrected a legendary 1921 exhibition of Constructivist art.
  21. Gough 1998, pp. 90–117
  22. In Snelson's article for Lalvani, 1996, I believe.
  23. David Georges Emmerich, Structures Tendues et Autotendantes, Paris: Ecole d'Architecture de Paris la Villette, 1988, pp. 30–31.
  24. Burkhardt, Robert William, Jr. (2008), A Practical Guide to Tensegrity Design (PDF)
  25. Sultan, Cornel; Martin Corless; Robert E. Skelton (2001). "The prestressability problem of tensegrity structures: some analytical solutions" (PDF). International Journal of Solids and Structures. 26: 145. Archived from the original (PDF) on 23 October 2015.
  26. Fuller, R. Buckminster (22 October 2010), Vector Equilibrium, retrieved 22 February 2019
  27. Verheyen, H.F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers & Mathematics with Applications. 17, 1–3 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0.
  28. "Tensegrity Figuren". Universität Regensburg. Archived from the original on 26 May 2013. Retrieved 2 April 2013.
  29. Coxeter, H.S.M. (1973) [1948]. "3.7 Coordinates for the vertices of the regular and quasi-regular solids". Regular Polytopes (3rd ed.). New York: Dover. pp. 51–52.

Bibliography

Further reading
  • Edmondson, Amy (2007). "A Fuller Explanation", Emergent World LLC
  • Forbes, Peter (2010) [2006]. "9. The Push and Pull Building System". The Gecko's Foot: How Scientists are Taking a Leaf from Nature's Book. Harper Collins. pp. 197–230. ISBN 978-0-00-740547-3.
  • Hanaor, Ariel (1997). "13. Tensegrity: Theory and Application". In Gabriel, J. François (ed.). Beyond the Cube: The Architecture of Space Frames and Polyhedra. Wiley. pp. 385–408. ISBN 978-0-471-12261-6.
  • Kenner, Hugh (1976). Geodesic Math and How to Use It. University of California Press. ISBN 978-0520029248. 2003 reprint ISBN 0520239318. This is a good starting place for learning about the mathematics of tensegrity and building models.
  • Masic, Milenko; Skelton, Robert E.; Gill, Philip E. (August 2005). "Algebraic tensegrity form-finding". International Journal of Solids and Structures. 42 (16–17): 4833–58. doi:10.1016/j.ijsolstr.2005.01.014. They present the remarkable result that any linear transformation of a tensegrity is also a tensegrity.
  • Morgan, G.J. (2003). "Historical Review: Viruses, Crystals and Geodesic Domes". Trends in Biochemical Sciences. 28 (2): 86–90. doi:10.1016/S0968-0004(02)00007-5. PMID 12575996.
  • Motro, R. (1992). "Tensegrity Systems: The State of the Art". International Journal of Space Structures. 7 (2): 75–84. doi:10.1177/026635119200700201. S2CID 107820090.
  • Pugh, Anthony (1976). An Introduction to Tensegrity. University of California Press. ISBN 978-0-520-03055-8. Archived from the original on 4 May 2008. Retrieved 9 May 2008.
  • Snelson, Kenneth (November 1990). "Letter to R. Motro". International Journal of Space Structures.
  • Souza, Thales R.; Fonseca, Sérgio T.; Gonçalves, Gabriela G.; Ocarino, Juliana M.; Mancini, Marisa C. (October 2009). "Prestress revealed by passive co-tension at the ankle joint". Journal of Biomechanics. 42 (14): 2374–80. doi:10.1016/j.jbiomech.2009.06.033. PMID 19647832.
  • Vilnay, Oren (1990). Cable Nets and Tensegric Shells: Analysis and Design Applications, New York: Ellis Horwood Ltd.
  • Wang, Bin-Bing (1998). "Cable-strut systems: Part I – Tensegrity". Journal of Constructional Steel Research. 45 (3): 281–89. doi:10.1016/S0143-974X(97)00075-8.
  • Wilken, Timothy (2001). Seeking the Gift Tensegrity, TrustMark
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.