Two ears theorem

In geometry, the two ears theorem states that every simple polygon with more than three vertices has at least two ears, vertices that can be removed from the polygon without introducing any crossings. The two ears theorem is equivalent to the existence of polygon triangulations. It is frequently attributed to Gary H. Meisters, but was proved earlier by Max Dehn.

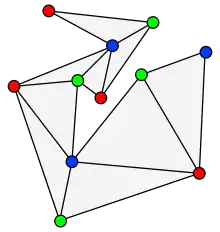
A triangulated polygon. The two vertices at the ends of the chain of triangles form ears. However, this polygon also has other ears that are not evident in this triangulation.

Statement of the theorem

An ear of a polygon is defined as a vertex v such that the line segment between the two neighbors of v lies entirely in the interior of the polygon. The two ears theorem states that every simple polygon has at least two ears.

Ears from triangulations

An ear and its two neighbors form a triangle within the polygon that is not crossed by any other part of the polygon. Removing a triangle of this type produces a polygon with fewer sides, and repeatedly removing ears allows any simple polygon to be triangulated.

Conversely, if a polygon is triangulated, the weak dual of the triangulation (a graph with one vertex per triangle and one edge per pair of adjacent triangles) will be a tree and each leaf of the tree will form an ear. Since every tree with more than one vertex has at least two leaves, every triangulated polygon with more than one triangle has at least two ears. Thus, the two ears theorem is equivalent to the fact that every simple polygon has a triangulation.[1]

An ear is called exposed when it forms a vertex of the convex hull of the polygon. However, it is possible for a polygon to have no exposed ears.[2]

Ears are a special case of a principal vertex, a vertex such that the line segment connecting the vertex's neighbors does not cross the polygon or touch any other vertex of it. A principal vertex for which this line segment lies outside the polygon is called a mouth. Analogously to the two ears theorem, every non-convex simple polygon has at least one mouth. Polygons with the minimum number of principal vertices of both types, two ears and a mouth, are called anthropomorphic polygons.[3]

History and proof

The two ears theorem is often attributed to a 1975 paper by Gary H. Meisters, from which the "ear" terminology originated.[4] However, the theorem was proved earlier by Max Dehn (circa 1899) as part of a proof of the Jordan curve theorem. To prove the theorem, Dehn observes that every polygon has at least three convex vertices. If one of these vertices, v, is not an ear, then it can be connected by a diagonal to another vertex x inside the triangle uvw formed by v and its two neighbors; x can be chosen to be the vertex within this triangle that is farthest from line uw. This diagonal decomposes the polygon into two smaller polygons, and repeated decomposition by ears and diagonals eventually produces a triangulation of the whole polygon, from which an ear can be found as a leaf of the dual tree.[5]

References
  1. O'Rourke, Joseph (1987), Art Gallery Theorems and Algorithms, International Series of Monographs on Computer Science, Oxford University Press, ISBN 0-19-503965-3, MR 0921437.
  2. Meisters, G. H. (1980), "Principal vertices, exposed points, and ears", American Mathematical Monthly, 87 (4): 284–285, doi:10.2307/2321563, MR 0567710.
  3. Toussaint, Godfried (1991), "Anthropomorphic polygons", American Mathematical Monthly, 98 (1): 31–35, doi:10.2307/2324033, MR 1083611.
  4. Meisters, G. H. (1975), "Polygons have ears", American Mathematical Monthly, 82: 648–651, doi:10.2307/2319703, MR 0367792.
  5. Guggenheimer, H. (1977), "The Jordan curve theorem and an unpublished manuscript by Max Dehn" (PDF), Archive for History of Exact Sciences, 17 (2): 193–200, doi:10.1007/BF02464980, JSTOR 41133486, MR 0532231.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.