Andreev reflection

Andreev reflection (AR), named after the Russian physicist Alexander F. Andreev, is a type of particle scattering which occurs at interfaces between a superconductor (S) and a normal state material (N). It is a charge-transfer process by which normal current in N is converted to supercurrent in S. Each Andreev reflection transfers a charge 2e across the interface, avoiding the forbidden single-particle transmission within the superconducting energy gap.

An electron (red) meeting the interface between a normal conductor (N) and a superconductor (S) produces a Cooper pair in the superconductor and a retroreflected hole (green) in the normal conductor. Vertical arrows indicate the spin band occupied by each particle.

Overview

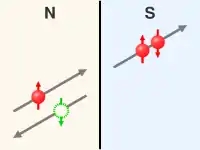
The process involves an electron (hole) incident on the interface from the normal state material at energies less than the superconducting energy gap. The incident electron (hole) forms a Cooper pair in the superconductor with the retroreflection of a hole (electron) of opposite spin and velocity but equal momentum to the incident electron (hole), as seen in the figure. The barrier transparency is assumed to be high, with no oxide or tunnel layer which reduces instances of normal electron-electron or hole-hole scattering at the interface. Since the pair consists of an up and down spin electron, a second electron (hole) of opposite spin to the incident electron (hole) from the normal state forms the pair in the superconductor, and hence the retroreflected hole (electron). Through time-reversal symmetry, the process with an incident electron will also work with an incident hole (and retroreflected electron).

The process is highly spin-dependent – if only one spin band is occupied by the conduction electrons in the normal-state material (i.e. it is fully spin-polarized), Andreev reflection will be inhibited due to inability to form a pair in the superconductor and impossibility of single-particle transmission. In a ferromagnet or material where spin-polarization exists or may be induced by a magnetic field, the strength of the Andreev reflection (and hence conductance of the junction) is a function of the spin-polarization in the normal state.

The spin-dependence of AR gives rise to the Point Contact Andreev Reflection (or PCAR) technique, whereby a narrow superconducting tip (often niobium, antimony or lead) is placed into contact with a normal material at temperatures below the critical temperature of the tip. By applying a voltage to the tip, and measuring differential conductance between it and the sample, the spin polarization of the normal metal at that point (and magnetic field) may be determined. This is of use in such tasks as measurement of spin-polarized currents or characterizing spin polarization of material layers or bulk samples, and the effects of magnetic fields on such properties.

In an AR process, the phase difference between the electron and hole is −π/2 plus the phase of the superconducting order parameter.

Crossed Andreev reflection

Crossed Andreev reflection, or CAR, also known as non-local Andreev reflection occurs when two spatially separated normal state material electrodes form two separate junctions with a superconductor, with the junction separation of the order of the BCS superconducting coherence length of the material in question. In such a device, retroreflection of the hole from an Andreev reflection process, resulting from an incident electron at energies less than the superconducting gap at one lead, occurs in the second spatially separated normal lead with the same charge transfer as in a normal AR process to a Cooper pair in the superconductor.[1] For CAR to occur, electrons of opposite spin must exist at each normal electrode (so as to form the pair in the superconductor). If the normal material is a ferromagnet this may be guaranteed by creating opposite spin polarization via the application of a magnetic field to normal electrodes of differing coercivity.

CAR occurs in competition with elastic cotunelling or EC, the quantum mechanical tunneling of electrons between the normal leads via an intermediate state in the superconductor. This process conserves electron spin. As such, a detectable CAR potential at one electrode on the application of current to the other may be masked by the competing EC process, making clear detection difficult. In addition, normal Andreev reflection may occur at either interface, in conjunction with other normal electron scattering processes from the normal/superconductor interface.

The process is of interest in the formation of solid-state quantum entanglement, via the formation of a spatially separated entangled electron-hole (Andreev) pair, with applications in spintronics and quantum computing.

References
  1. Guiseppe Falci; Denis Feinberg; Frank Hekking (April 2001). "Correlated tunneling into a superconductor in a multiprobe hybrid structure". Europhysics Letters. 54 (2): 255–261. arXiv:cond-mat/0011339. Bibcode:2001EL.....54..255F. doi:10.1209/epl/i2001-00303-0.

Further reading
Books
  • de Gennes, P. G. (1966). Superconductivity of Metals and Alloys. New York: W. A. Benjamin. ISBN 978-0-7382-0101-6.
  • Tinkham, M (2004). Introduction to Superconductivity (Second ed.). New York: Dover. ISBN 978-0-486-43503-9.
Papers
  • Andreev, A. F. (1964). "Thermal conductivity of the intermediate state of superconductors". Sov. Phys. JETP. 19: 1228.
  • Blonder, G. E.; Tinkham, M.; Klapwijk, T. M. (1982). "Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion". Phys. Rev. B. 25 (7): 4515. Bibcode:1982PhRvB..25.4515B. doi:10.1103/PhysRevB.25.4515.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.