Borda count

The Borda count is a family of single-winner election methods in which voters rank options or candidates in order of preference. The Borda count determines the outcome of a debate or the winner of an election by giving each candidate, for each ballot, a number of points corresponding to the number of candidates ranked lower. Once all votes have been counted, the option or candidate with the most points is the winner. The Borda count is intended to elect broadly acceptable options or candidates, rather than those preferred by a majority, and so is often described as a consensus-based voting system rather than a majoritarian one.[1]

Part of the Politics series
Electoral Systems
Plurality/majoritarian
  • Multi-round voting
Proportional representation
Mixed systems
Other systems and related theory
 Politics portal

The modified Borda count is a variant used for decision-making. For multi-winner elections, especially when proportional representation is important, the quota Borda system may be used.

The Borda count was developed independently several times, being first proposed in 1435 by Nicholas of Cusa (see History below),[2][3][4][5] but is named for the 18th-century French mathematician and naval engineer Jean-Charles de Borda, who devised the system in 1770. It is currently used to elect two ethnic minority members of the National Assembly of Slovenia,[6] in modified forms to determine which candidates are elected to the party list seats in Icelandic parliamentary elections, and for selecting presidential election candidates in Kiribati. A variant known as the Dowdall system is used to elect members of the Parliament of Nauru.[7] Until the early 1970s, another variant was used in Finland to select individual candidates within party lists. It is also used throughout the world by various private organizations and competitions.

Voting and counting

Ballot

The Borda count is a preferential, or ranked, voting system; the voter ranks the list of candidates in order of preference. So, for example, the voter gives a 1 to their most preferred candidate, a 2 to their second most preferred, and so on. In this respect, it is the same as elections under systems such as instant-runoff voting, the single transferable vote or Condorcet methods. The integer-valued ranks for evaluating the candidates were justified by Laplace, who used a probabilistic model based on the law of large numbers.[5]

The Borda count is classified as a positional voting system. Other positional methods include first-past-the-post voting, bloc voting, approval voting and limited voting.

There are a number of ways of scoring candidates under the system, and it has a variant (the Dowdall system) which is significantly different.

Tournament-style counting

Each candidate is assigned a number of points from each ballot equal to the number of candidates to whom he or she is preferred, so that with n candidates, each one receives n − 1 points for a first preference, n − 2 for a second, and so on.[8] The winner is the candidate with the largest total number of points. For example, in a four-candidate election, the number of points assigned for the preferences expressed by a voter on a single ballot paper might be:

RankingCandidateFormulaPointsRelative points
1st Andrewn − 131.00
2nd Briann − 220.67
3rd Catherinen − 310.33
4th Davidn − 400.00

A detailed example, based on a fictitious election for Tennessee state capital, is shown below.

Borda's original counting

As Borda proposed the system, each candidate received one more point for each ballot cast than in tournament-style counting. Thus in the example Andrew would receive 4 points, and David 1 point. This counting method is used in the Slovenian parliamentary elections for 2 out of 90 seats.[7]

Tournament-style counting will be assumed in the remainder of this article.

Dowdall system (Nauru)

The island nation of Nauru uses a variant called the Dowdall system:[9][7] the voter awards the first-ranked candidate with 1 point, while the 2nd-ranked candidate receives ½ a point, the 3rd-ranked candidate receives ⅓ of a point, etc. (A similar system of weighting lower-preference votes was used in the 1925 Oklahoma primary electoral system.) Using the above example, in Nauru the point distribution among the four candidates would be this:

RankingCandidateFormulaPointsAbsolute points
1st Andrew1/11.0012
2nd Brian1/20.506
3rd Catherine1/30.334
4th David1/40.253

This method is more favorable to candidates with many first preferences than the conventional Borda count. It has been described as a system "somewhere between plurality and the Borda count, but as veering more towards plurality".[7] Simulations show that 30% of Nauru elections would produce different outcomes if counted using standard Borda rules.[7]

The system was devised by Nauru’s Secretary for Justice, Desmond Dowdall, an Irishman, in 1971.[7]

Counting of ties

Several different methods of handling ties have been suggested.

Tournament-style counting of ties

Tournament-style counting can be extended to allow ties anywhere in a voter’s ranking by assigning each candidate half a point for every other candidate he or she is tied with, in addition to a whole point for every candidate he or she is strictly preferred to.

In the example, suppose that a voter is indifferent between Andrew and Brian, preferring both to Catherine and Catherine to David. Then Andrew and Brian will each receive 2½ points, Catherine will receive 1, and David none. This is referred to as "averaging" by Narodytska and Walsh.[10]

Borda’s original counting of ties

In Borda’s system as originally proposed, ties were allowed only at the end of a voter’s ranking, and each tied candidate was given the minimum number of points. So if a voter marks Andrew as his or her first preference, Brian as his or her second, and leaves Catherine and David unranked (called "truncating the ballot"), then Andrew will receive 3 points, Brian 2, and Catherine and David none. This is an example of what Narodytska and Walsh call "rounding down".

Modified Borda count

The "modified Borda count" again allows ties only at the end of a voter’s ranking. It gives no points to unranked candidates, 1 point to the least preferred of the ranked candidates, etc. So if a voter ranks Andrew above Brian and leaves other candidates unranked, Andrew will receive 2 points, Brian will receive 1 point, and Catherine and David will receive none. This is equivalent to "rounding up". The most preferred candidate on a ballot paper will receive a different number of points depending on how many candidates were left unranked.

Comparison of methods of counting ties

Rounding down penalises unranked candidates (they share fewer points than they would if they were ranked), while rounding up rewards them. Both methods encourage undesirable behaviour from voters.

First example (bias of rounding up)

Suppose that there are two candidates: A with 100 supporters and C with 80. A will win by 100 points to 80.

Now suppose that a third candidate B is introduced, who is a clone of C, and that the modified Borda count is used. Voters who prefer B and C to A have no way of indicating indifference between them, so they will choose a first preference at random, voting either B-C-A or C-B-A. Supporters of A can show a tied preference between B and C by leaving them unranked. B and C will each receive about 120 votes, while A receives 100.

But if A can persuade his supporters to rank B and C randomly, he will win with 200 points, while B and C each receive about 170.

If ties were averaged (i.e. used tournament counting), then the appearance of B as a clone of C would make no difference to the result; A would win as before, regardless of whether voters truncated their ballots or made random choices between B and C.

Second example (bias of rounding down)

A similar example can be constructed to show the bias of rounding down. Suppose that A and C are as before, but that B is now a near-clone of A, preferred to A by male voters but rated lower by females. About 50 voters will vote A-B-C, about 50 B-A-C, about 40 C-A-B and about 40 C-B-A. A and B will each receive about 190 votes, while C will receive 160.

But ties are resolved according to Borda’s proposal, and if C can persuade her supporters to leave A and B unranked, then there will be about 50 A-B-C ballots, about 50 B-A-C and 80 truncated to just C. A and B will each receive about 150 votes, while C receives 160.

Again, if tournament counting of ties was used, truncating ballots would make no difference, and the winner would be either A or B.

Interpretation of examples of ties

Borda’s method has often been accused of being susceptible to tactical voting, which is partly due to its association with biased methods of handling ties. The French Academy of Sciences (of which Borda was a member) experimented with Borda’s system, but abandoned it, in part because “the voters found how to manipulate the Borda rule: not only by putting their most dangerous rival at the bottom of their lists, but also by truncating their lists”.[11] In response to the issue of strategic manipulation in the Borda count, M. de Borda said: “My scheme is intended for only honest men”.[8][11]

Tactical voting is common in Slovenia, where truncated ballots are allowed; a majority of voters bullet-vote, with only 42% of voters ranking a second-preference candidate. As with Borda’s original proposal, ties are handled by rounding down (or sometimes by ultra-rounding, unranked candidates being given one less point than the minimum for ranked candidates).[7]

Ties in the Dowdall system

Ties are not allowed: Nauru voters are required to rank all candidate, and ballots that fail to do so are rejected.[7]

Properties

Elections as estimation procedures

Condorcet looked at an election as an attempt to combine estimators. Suppose that each candidate has a figure of merit and that each voter has a noisy estimate of the value of each candidate. The ballot paper allows the voter to rank the candidates in order of estimated merit. The aim of the election is to produce a combined estimate of the best candidate. Such an estimator can be more reliable than any of its individual components. Applying this principle to jury decisions, Condorcet derived his theorem that a large enough jury would always decide correctly.[12]

Peyton Young showed that the Borda count gives an approximately maximum likelihood estimator of the best candidate.[13] His theorem assumes that errors are independent, in other words, that if a voter Veronica rates a particular candidate highly, then there is no reason to expect her to rate "similar" candidates highly. If this property is absent – if Veronica gives correlated rankings to candidates with shared attributes – then the maximum likelihood property is lost, and the Borda count is subject to nomination effects: a candidate is more likely to be elected if there are similar candidates on the ballot.

Young showed that the Kemeny–Young method was the exact maximum likelihood estimator. It also satisfies the Condorcet criterion but is computationally burdensome.

Effect of irrelevant alternatives

The property of independence of irrelevant alternatives is possessed by any voting method for which a preference between A and B is not affected by the entry of a third candidate C into the election. Standard voting systems do not generally have this property, but many possess it in the special case when opinions lie along a spectrum and when voters rank candidates in order of proximity. Voting systems that satisfy the Condorcet criterion automatically also satisfy the median voter theorem, which applies to votes along a spectrum and says that the winner of an election will be the candidate preferred by the median voter, regardless of which other candidates stand.

Even in this weaker form the Borda count does not achieve independence of irrelevant alternatives. Suppose that there are 11 voters whose positions along the spectrum can be written 0, 1, ..., 10, and suppose that there are 2 candidates, Andrew and Brian, whose positions are as shown:

Candidate A B
Position 5¼ 6¼

The median voter Marlene is at position 5, and both candidates are to her right, so we would expect A to be elected. We can verify this for the Borda system by constructing a table to illustrate the count. The main part of the table shows the voters who prefer the first to the second candidate, as given by the row and column headings, while the additional column to the right gives the scores for the first candidate.

2nd
1st
 AB score
A —0–56
B 6–10—5

A is indeed elected, as he would be under any reasonable system.

But now suppose that two additional candidates, further to the right, enter the election.

Candidate A B C D
Position 5¼ 6¼ 8¼ 10¼

The counting table expands as follows:

2nd
1st
 ABCD score
A —0–50–60–721
B 6–10—0–70–822
C 7–108–10—0–917
D 8–109–1010—6

The entry of two dummy candidates allows B to win the election.

This example bears out the comment of the Marquis de Condorcet, who argued that the Borda count "relies on irrelevant factors to form its judgments" and was consequently "bound to lead to error".[7]

Other properties

There are a number of formalised voting system criteria whose results are summarised in the following table.

Comparison of preferential electoral systems
Sys­tem Mono­tonic Cond­orcet Majo­rity Condorcet loser Majority loser Mutual majority Smith ISDA LIIA Independence of clones Reversal symmetry Participation, consistency Later-no‑harm Later-no‑help Polynomial time Resol­vability
Schulze YesYesYesYesYesYesYesYesNoYesYesNoNoNoYesYes
Ranked pairs YesYesYesYesYesYesYesYesYesYesYesNoNoNoYesYes
Tideman's Alternative NoYesYesYesYesYesYesYesNoYesNoNoNoNoYesYes
Kemeny–Young YesYesYesYesYesYesYesYesYesNoYesNoNoNoNoYes
Copeland YesYesYesYesYesYesYesYesNoNoYesNoNoNoYesNo
Nanson NoYesYesYesYesYesYesNoNoNoYesNoNoNoYesYes
Black YesYesYesYesYesNoNoNoNoNoYesNoNoNoYesYes
Instant-runoff voting NoNoYesYesYesYesNoNoNoYesNoNoYesYesYesYes
Smith/IRV NoYesYesYesYesYesYesYesNoYesNoNoNoNoYesYes
Borda YesNoNoYesYesNoNoNoNoNoYesYesNoYesYesYes
Baldwin NoYesYesYesYesYesYesNoNoNoNoNoNoNoYesYes
Bucklin YesNoYesNoYesYesNoNoNoNoNoNoNoYesYesYes
Plurality YesNoYesNoNoNoNoNoNoNoNoYesYesYesYesYes
Contingent voting NoNoYesYesYesNoNoNoNoNoNoNoYesYesYesYes
Coombs[14] NoNoYesYesYesYesNoNoNoNoNoNoNoNoYesYes
MiniMax YesYesYesNoNoNoNoNoNoNoNoNoNoNoYesYes
Anti-plurality[14] YesNoNoNoYesNoNoNoNoNoNoYesNoNoYesYes
Sri Lankan contingent voting NoNoYesNoNoNoNoNoNoNoNoNoYesYesYesYes
Supplementary voting NoNoYesNoNoNoNoNoNoNoNoNoYesYesYesYes
Dodgson[14] NoYesYesNoNoNoNoNoNoNoNoNoNoNoNoYes

Simulations show that Borda has a high probability of choosing the Condorcet winner when one exists.[7]

Truncated ballots

Some implementations of Borda voting require voters to truncate their ballots to a certain length:

  • In Kiribati, a variant is employed which uses a traditional Borda formula, but in which voters rank only four candidates, irrespective of how many are standing.[15]
  • In Toastmasters International, speech contests are truncation-scored as 3, 2, 1 for the top-three ranked candidates. Ties are broken by having a special ballot that is ignored unless there is a tie.[16]

Multiple winners

The system invented by Borda was intended for use in elections with a single winner, but it is also possible to conduct a Borda count with more than one winner, by recognizing the desired number of candidates with the most points as the winners. In other words, if there are two seats to be filled, then the two candidates with most points win; in a three-seat election, the three candidates with most points, and so on. In Nauru, which uses the multi-seat variant of the Borda count, parliamentary constituencies of two and four seats are used. The quota Borda system is a system of proportional representation in multi-seat constituencies that uses the Borda count.

Other systems

A number of other voting systems employ the Borda system of assigning points for rankings. The Nanson and Baldwin methods are single-winner voting systems that combine elements of the Borda count and instant-runoff voting. Unlike the Borda count, Nanson and Baldwin are majoritarian and Condorcet methods, because they use the fact that a Condorcet winner always has a higher-than-average Borda score relative to other candidates, and the Condorcet loser a lower-than-average Borda score. [17]

As a consensual method

Unlike other popular voting systems, in the Borda count it is possible that a candidate who is the first preference of an absolute majority of voters will not be elected; this is because the Borda count affords greater importance to a voter's lower preferences than most other systems, including other preferential methods such as instant-runoff voting and Condorcet methods.

The Borda count tends to favor candidates supported by a broad consensus among voters, rather than the candidate who is necessarily the favorite of a majority;[1] for this reason, its supporters see the Borda count as a method that promotes unity and avoids the 'tyranny of the majority', and the resulting divisiveness and even violence that it can lead to. Advocates argue, for example, that where the majority candidate is strongly opposed by a large minority of the electorate, the Borda winner may have higher overall utility than the majority winner. On grounds such as these, the de Borda Institute of Northern Ireland advocates the use of a form of referendum based on the Borda count in divided societies such as Northern Ireland, the Balkans and Kashmir.[18][19]

Because it will not necessarily elect a candidate who is the first preference of a majority of voters, the Borda count is said by scholars to fail the majority criterion. Other voting systems that favor consensus rather than majority rule include cardinal methods such as approval voting, score voting, and their variants.[20] These are sometimes called "utilitarian voting methods" because they try to maximize the entire population's utility, rather than maximizing the majority's utility at the expense of the minority.[21][22][23]

Example

Consider an election in which 100 voters express the following preferences:

No. 51 voters 5 voters 23 voters 21 voters
1st Andrew Catherine Brian David
2nd Catherine Brian Catherine Catherine
3rd Brian David David Brian
4th David Andrew Andrew Andrew

The scores of the candidates are:

CandidateBorda scoreDowdall scoreFPTP votes (plurality)Copeland score
Andrew15363.25513
Brian15149.5231
Catherine20552.552
David9143.0833210

Under most single-winner voting systems – including first-past-the-post (plurality), instant-runoff, Condorcet methods, and Dowdall – Andrew would have been the winning candidate; however, under the Borda count Catherine has the highest score and so is elected instead. Although Andrew is supported by an unambiguous absolute majority of voters, he is the last preference of 49 voters, which suggests that he may be strongly opposed by almost one half of the electorate. Catherine, though she receives only a handful of first-preference votes, is at least the second choice of all voters, implying that she is broadly acceptable to all.

The Dowdall system places a stronger emphasis on first choices than does the Borda count, which is why Catherine did so poorly under it.

The conclusion from this example is at variance from what is implied by the earlier example concerning the effect of irrelevant alternatives. A possible interpretation is that in the earlier example the voters were assigned numerical values, allowing a consensus position to be recognised without reference to the candidates standing, whereas in this case the consensus needs to be inferred from the preferences given to the candidates, which can’t be done reliably. It may be that B, C and D are near-clones.

Potential for tactical manipulation
See also: Tactical voting § Borda

Tactical voting

Like many other voting systems, the Borda count is vulnerable to tactical voting. In particular, it is susceptible to the tactics of compromising and burying. In compromising, voters can benefit by insincerely raising the position of their second choice candidate over their first choice candidate, in order to help the second choice candidate to beat a candidate they like even less. In burying, voters can help a more-preferred candidate by insincerely lowering the position of a less-preferred candidate on their ballot.

An effective tactic is to combine these two strategies. For example, if there are two candidates whom a voter considers to be the most likely to win, the voter can maximise his impact on the contest between these front runners by ranking the candidate whom he likes more in first place, and ranking the candidate whom he likes less in last place. If neither front runner is his sincere first or last choice, the voter is employing both the compromising and burying tactics at once; if many voters employ such strategies, then the result will no longer reflect the sincere preferences of the electorate.

Using the example below based on choosing the capital of Tennessee, if polls suggest a toss-up between Nashville and Chattanooga, citizens of Knoxville might change their ranking to

  1. Chattanooga (compromising their sincere first choice, Knoxville)
  2. Knoxville
  3. Memphis (burying their sincere third choice, Nashville)
  4. Nashville

If many Knoxville voters voted in this way, it would result in the election of Chattanooga. Citizens of Chattanooga could also increase the likelihood of the election of their city by voting tactically, but would require the assistance of some tactical voters from Knoxville to be successful.

Strategic nomination

The Borda count is highly vulnerable to a form of strategic nomination called teaming or cloning. This means that when more candidates run with similar ideologies, the probability of one of those candidates winning increases. This is illustrated by an example above. Therefore, under the Borda count, it is to a faction's advantage to run as many candidates in that faction as they can. For example, even in a single-seat election, it would be to the advantage of a political party to stand as many candidates as possible in an election. In this respect, the Borda count differs from many other single-winner systems, such as the 'first past the post' plurality system, in which a political faction is disadvantaged by running too many candidates. Under systems such as plurality, 'splitting' a party's vote in this way can lead to the spoiler effect, which harms the chances of any of a faction's candidates being elected.

Strategic nomination is used in Nauru, according to MP Roland Kun, with factions running multiple "buffer candidates" who are not expected to win, to lower the tallies of their main competitors.[7]

Example

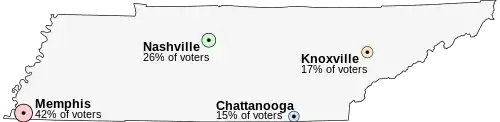
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

  • Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
  • Nashville, with 26% of the voters, near the center of the state
  • Knoxville, with 17% of the voters
  • Chattanooga, with 15% of the voters

The preferences of the voters would be divided like this:

42% of voters
(close to Memphis)		 26% of voters
(close to Nashville)		 15% of voters
(close to Chattanooga)		 17% of voters
(close to Knoxville)
  1. Memphis
  2. Nashville
  3. Chattanooga
  4. Knoxville
  1. Nashville
  2. Chattanooga
  3. Knoxville
  4. Memphis
  1. Chattanooga
  2. Knoxville
  3. Nashville
  4. Memphis
  1. Knoxville
  2. Chattanooga
  3. Nashville
  4. Memphis

This leads to the following point counts per 100 voters:

Voters' home cityMemphisNashvilleKnoxvilleChattanooga
Memphis42×3=12642×2=84042×1=42
Nashville026×3=7826×1=2626×2=52
Knoxville017×1=1717×3=5117×2=34
Chattanooga015×1=1515×2=3015×3=45
Total126194107173

Thus Nashville is elected.

Current uses

Political uses

The Borda count is used for certain political elections in at least three countries, Slovenia and the tiny Micronesian nations of Kiribati and Nauru.

In Slovenia, the Borda count is used to elect two of the ninety members of the National Assembly: one member represents a constituency of ethnic Italians, the other a constituency of the Hungarian minority.

Members of the Parliament of Nauru are elected based on a variant of the Borda count that involves two departures from the normal practice: (1) multi-seat constituencies, of either two or four seats, and (2) a point-allocation formula that involves increasingly small fractions of points for each ranking, rather than whole points.

In Kiribati, the president (or Beretitenti) is elected by the plurality system, but a variant of the Borda count is used to select either three or four candidates to stand in the election. The constituency consists of members of the legislature (Maneaba). Voters in the legislature rank only four candidates, with all other candidates receiving zero points. Since at least 1991, tactical voting has been an important feature of the nominating process.

The Republic of Nauru became independent from Australia in 1968. Before independence, and for three years afterwards, Nauru used instant-runoff voting, importing the system from Australia, but since 1971, a variant of the Borda count has been used.

The modified Borda count has been used by the Green Party of Ireland to elect its chairperson.[24][25]

The Borda count has been used for non-governmental purposes at certain peace conferences in Northern Ireland, where it has been used to help achieve consensus between participants including members of Sinn Féin, the Ulster Unionists, and the political wing of the UDA.

Other uses

The Borda count is used in elections by some educational institutions in the United States:

The Borda count is used in elections by some professional and technical societies:

The OpenGL Architecture Review Board uses the Borda count as one of the feature-selection methods.

The Borda count is used to determine winners for the World Champion of Public Speaking contest organized by Toastmasters International. Judges offer a ranking of their top three speakers, awarding them three points, two points, and one point, respectively. All unranked candidates receive zero points.

The modified Borda count is used to elect the President for the United States member committee of AIESEC.

The Eurovision Song Contest uses a heavily modified form of the Borda count, with a different distribution of points: only the top ten entries are considered in each ballot, the favorite entry receiving 12 points, the second-placed entry receiving 10 points, and the other eight entries getting points from 8 to 1. Although designed to favor a clear winner, it has produced very close races and even a tie.

The Borda count is used for wine trophy judging by the Australian Society of Viticulture and Oenology, and by the RoboCup autonomous robot soccer competition at the Center for Computing Technologies, in the University of Bremen in Germany.

The Finnish Associations Act lists three different modifications of the Borda count for holding a proportional election. All the modifications use fractions, as in Nauru. A Finnish association may choose to use other methods of election, as well.[27]

Sports

The Borda count is a popular method for granting sports awards in the United States. Uses include:

In sailboat fleet racing, the Borda count is used to select the winner of a regatta, with each individual race in the regatta treated as a 'vote'.

History

A form of the Borda count was one of the voting methods employed in the Roman Senate beginning around the year 105. However, in its modern, mathematical form, the system is thought to have been discovered independently at least three times:

See also

Notes
  1. Lippman, David. "Voting Theory" (PDF). Math in Society. Borda count is sometimes described as a consensus-based voting system, since it can sometimes choose a more broadly acceptable option over the one with majority support.
  2. Emerson, Peter (16 January 2016). From Majority Rule to Inclusive Politics. Springer. ISBN 9783319235004.
  3. Emerson, Peter (1 February 2013). "The original Borda count and partial voting". Social Choice and Welfare. 40 (2): 353–358. doi:10.1007/s00355-011-0603-9. ISSN 0176-1714. S2CID 29826994.
  4. Actually, Nicholas' system used higher numbers for more-preferred candidates.
  5. Tangian, Andranik (2020). Analytical theory of democracy. Vols. 1 and 2. Cham, Switzerland: Springer. pp. 99–101, 132ff. ISBN 978-3-030-39690-9.
  6. "Slovenia's electoral law". Archived from the original on 4 March 2016. Retrieved 15 June 2009.
  7. Fraenkel, Jon; Grofman, Bernard (3 April 2014). "The Borda Count and its real-world alternatives: Comparing scoring rules in Nauru and Slovenia". Australian Journal of Political Science. 49 (2): 186–205. doi:10.1080/10361146.2014.900530. S2CID 153325225.
  8. Black, Duncan (1987) [1958]. The Theory of Committees and Elections. Springer Science & Business Media. ISBN 9780898381894.
  9. Reilly, Benjamin (2002). "Social Choice in the South Seas: Electoral Innovation and the Borda Count in the Pacific Island Countries". International Political Science Review. 23 (4): 364–366. CiteSeerX 10.1.1.924.3992. doi:10.1177/0192512102023004002. S2CID 3213336.
  10. Nina Narodytska and Toby Walsh, "The Computational Impact of Partial Votes on Strategic Voting" (2014).
  11. McLean, Iain; Urken, Arnold B.; Hewitt, Fiona (1995). Classics of Social Choice. University of Michigan Press. ISBN 978-0472104505.
  12. Eric Pacuit, “Voting Methods”, The Stanford Encyclopedia of Philosophy (Fall 2019 Edition), Edward N. Zalta (ed.).
  13. H. P. Young, "Condorcet’s Theory of Voting" (1988).
  14. Anti-plurality, Coombs and Dodgson are assumed to receive truncated preferences by apportioning possible rankings of unlisted alternatives equally; for example, ballot A > B = C is counted as  A > B > C and  A > C > B. If these methods are assumed not to receive truncated preferences, then later-no-harm and later-no-help are not applicable.
  15. Reilly, Benjamin. "Social Choice in the South Seas: Electoral Innovation and the Borda Count in the Pacific Island Countries" (PDF). Archived from the original (PDF) on 19 August 2006.
  16. SPEECH CONTEST RULEBOOK JULY 1, 2017 TO JUNE 30, 2018
  17. https://www.cs.rpi.edu/~xial/COMSOC18/papers/COMSOC2018_paper_33.pdf
  18. Emerson, Peter (2016). From Majority Rule to Inclusive Politics (1st ed.). Cham: Springer. ISBN 9783319235004. OCLC 948558369. Unfortunately, one of the worst democratic structures is the most ubiquitous: majority rule based on majority voting. It must be emphasised, furthermore, that these two practices are often the catalysts of division and bitterness, if not indeed violence and war.
  19. Emerson, Peter (23 March 2016). "Majority Rule - A Cause of War?". In Gardner, Hall; Kobtzeff, Oleg (eds.). The Ashgate Research Companion to War: Origins and Prevention. Routledge. ISBN 9781317041108.
  20. "Majority Criterion". The Center for Election Science. 21 May 2015. Retrieved 3 December 2016. Sometimes a candidate who is the Condorcet winner, or even the majority winner, isn’t the favored or “most representative” candidate of the electorate.
  21. "Utilitarian vs. Majoritarian Election Methods". The Center for Election Science. Retrieved 13 May 2018.
  22. "Vote Aggregation Methods". lorrie.cranor.org. Retrieved 12 January 2017.
  23. Hillinger, Claude (15 May 2006). "The Case for Utilitarian Voting". Rochester, NY: Social Science Research Network. SSRN 878008. Cite journal requires |journal= (help)
  24. Voting Systems
  25. Emerson, Peter (2007) Designing an All-Inclusive Democracy. Springer Verlag, Part 1, pages 15-38 "Collective Decision-making: The Modified Borda Count, MBC" ISBN 978-3-540-33163-6 (Print) 978-3-540-33164-3 (Online)
  26. "Undergraduate Council Adopts New Voting Method for Elections | News | the Harvard Crimson".
  27. "Finnish Associations Act". National Board of Patents and Registration of Finland. Archived from the original on 1 March 2013. Retrieved 26 June 2011.
  28. Heisman.com - Heisman Trophy

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.